| Общая цель: | научить учащихся применять формулы сокращенного умножения при выполнении упражнений различной сложности и творческих заданий. 1) Образовательная: Повторить знание формул сокращённого умножения; Закрепить знание формул сокращённого умножения и их применение при упрощении выражений; Отработка вычислительных навыков; Формирование у учащихся мотивации к изучению предмета. 2) Развивающая: Формировать умение анализировать, Обобщать, развивать математическое мышление. Формировать навыки самоконтроля, адекватной самооценки и саморегуляции деятельности. 3) Воспитательная: Воспитание ответственности за выполненную работу; Воспитывать умение правильно оценивать результаты своего труда |
| Источники, оснащение и оборудование, ресурсы: | Слайдовая презентация, ресурсный материал, листы А3, цветные карандаши, карточки – тесты, оценочные листы с критериями |
| Организационный этап (3-5 мин)
| Мотивация: Здравствуйте, ребята! Я рада снова вас видеть. Давайте настроимся на работу. Я хочу вас попросить, чтоб каждый из вас пожелал друг другу успехов в сегодняшнем уроке. Садитесь. Тема сегодняшнего урока формулы сокращенного умножения. Прежде, чем приступить к работе, каждый из вас должен поставить перед собой цель сегодняшнего урока. Перед вами лежат оценочные листы, подпишите их. На каждом этапе урока вы будете оценивать себя, выставляя количество заработанных баллов от 1 до 5 в оценочные листы. Запишите в тетрадях число и тему урока. | “Я познание сделал своим ремеслом…” Фамилия и имя: ____________________________________________________________________________________________ | Задание № 1 «Установи соответствие» | Задание № 2 Тест. | Задание № 3 «Замени звезду» | Задание № 4 Игра “Алгебраическая мозаика” | Задание № 5 Дополнительное задание | итоги | | (групповая работа) Собрать формулу и назвать эту формулу и дать полное название | Для каждого выражения из левого столбца подберите ему тождественно равное в правом: | Замените 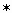 одночленом так, чтобы получившееся равенство было тождеством. одночленом так, чтобы получившееся равенство было тождеством. | Составить из предложенных выражений формулы. Кто больше.
| Применяя формулы сокращенного умножения решить уравнения
| Посчитать количество баллов за все задания | | «5» - все верно «4» - 1- 2 ошибки «3» - 3 ошибки | «5» - все верно «4» - 1- 2 ошибки «3» - 3 ошибки | «5» - все верно «4» - 1- 2 ошибки «3» - 3 ошибки | «5» - все верно «4» - 1- 2 ошибки «3» - 3 ошибки
| «5» - все верно «4» - 1- 2 ошибки «3» - 3 ошибки
| «25-20» оценка – 5 «19-15» оценка - 4 «14» оценка - 3 | | | Балл___________ | Балл ________ | Балл ________ | Балл _________ | Балл __________ | Оценка ___ |
| Достиг ли ты своих целей? Оцени степень усвоенности: | усвоил полностью усвоил частично не усвоил | | Продолжи одно из предложений: “Мне понятно…_____________________________________________________________________________________________________________________ “Я запомнил…__________________________________________________________________________________________________________________________ “Мне на уроке…____________________________________________________________________________________________________________________ “Я думаю…______________________________________________________________________________________________________________________________ |
|
| Настрой: ребята желают друг другу пожелания
Записывают число и тему урока Озвучивают цель урока Заполоняют оценочные листы
|
| Актуализация знаний. (10 мин) | Раздает карточки и объясняет правило «Установить соответствие» (групповая работа) Ребята, формулы сокращенного умножения имеют широкое применение в математике, особенно в старших классах. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений. Поэтому надо хорошо знать эти формулы и уметь применять их в преобразованиях выражений.
а) А сейчас мы начнем наш путь с повторения формул и правил. У вас на партах лежат разные карточки ваша задача составить из карточек формулы сокращенного умножения на листе А4. Выйти к доске и рассказать правило вашего кластера | 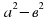 = (а – в)(а + в) = (а – в)(а + в) разность квадратов двух выражений | Разность квадратов двух выражений равна произведению их разности на их сумму. | | (а + в)2 = а2 + 2ав + в2
квадрат суммы двух выражений | Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. | | (а – в)2 = а2 – 2ав + в2
квадрат разности двух выражений | Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. | | (а + в)3 = а3 + 3а2 в + 3ав2 + в3
куб суммы двух выражений | Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, плюс куб второго выражения. | | (а – в)3 = а3 – 3а2 в + 3ав2 – в3 куб разности двух выражений | Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, минус куб второго выражения. | | а3 + в3 = (а + в)(а2 – ав + в2)
сумма кубов двух выражений | Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. | | а3 – в3 = (а – в)(а2 + ав + в2)
разность кубов двух выражений | Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы. | Если кластер составлен верно: группа заполняет оценочный лист от 1 – 5 баллов
| Ребята решают вместе в группе составляют из карточек формулы соответствие и заполняют оценочные листы |
| Обобщение и систематизация знаний. | Раздаю ресурсный материал Задание № 2 Тест. Расшифровка. Для каждого выражения из левого столбца подберите ему тождественно равное в правом: («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
| № формулы | формула | № ответа | ответ | буква | | 1 | (x+3)² | 1 | 4x²-9 | О | | 2 | x²-16 | 2 | 16x²-40xy+25y² | А | | 3 | (2x-3)(2x+3) | 3 | (x-4)(x+4) | И | | 4 | 81-18x+x² | 4 | (3y+6x)² | Т | | 5 | (4x-5y)² | 5 | x²+6x+9 | Д | | 6 | 25x²-49y² | 6 | (9-x)² | Ф | | 7 | 9y²+36yx+36x² | 7 | (5x-7y)(5x+7y) | Н | Каждый ученик получает карточку, выполняет задание, получает соответствия:
1→5(Д), 2→3(И), 3→1(О), 4→6(Ф), 5→2(А), 6→7(Н), 7→4(Т). Молодцы ребята, вы получили имя великого математика. Показываю его портрет.
Историческая справка: Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время, все алгебраические утверждения выражали в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения. Задание № 3 «Замени звезду» Замените 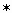 одночленом так, чтобы получившееся равенство было тождеством. (Индивидуальное задание.) («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки) одночленом так, чтобы получившееся равенство было тождеством. (Индивидуальное задание.) («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки) Ответы: | 1 | 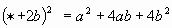
| a | | 2 | 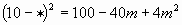
| 2m | | 3 | 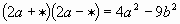
| 3b | | 4 | 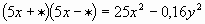
| 0,4y | | 5 | 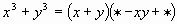
| х2, y2 | | 6 | 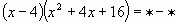
| х3, 64 | - Какими формулами вы пользовались в данном задании? ЗАДАНИЕ №4: Игра “Алгебраическая мозаика”. Составить из предложенных выражений формулы. Кто больше. 3х, 5у, 3х, 5у, 9х2, 30ху, 27х3, 125х2, 15ху, 25у2 , 125у3 . Ответы: (Всего 7 формул. («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки) (3х + 5у)2 = 3х2+30ху+25у2 (3х – 5у)(3х + 5у) = 9х2– 25у 2 27х3 + 125у3 = (3х + 5у)(9х2+ 15ху+25у2) (5у – 3х)2 = 25у2 – 30ху + 9х2 Задание № 5. Дополнительное (Работа с одаренными детьми) Решить уравнения | Решают задания по карточкам и выставляют оценки |
| Домашняя работа | Дифференцированная домашняя работа. Применив формулы сокращенного умножения, заполни таблицу: даны 5 пар выражений на «3» 3 любых пары, «4» - 4 пары, «5» заполнена вся таблица. Учить формулы и правила. | 1 и 2 выражения | Многочлен равный квадрату суммы этих выражений | Многочлен равный квадрату разности этих выражений | Многочлен равный кубу суммы этих выражений | Многочлен равный кубу разности этих выражений | Разность квадратов этих выражений | | -5а и b |
|
| | | | | 3а и 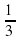 b b | | | | | | | 5а2 и 0,2b2 | | | | | | | a2b и –4 | | | | | | | 6 и х2у2 | | | | | |
| Учащиеся записывают в дневники домашнее задание и разбирают карточки |
| Подведение итогов (5 мин) Рефлексия | Итак, ребята урок подошел к концу. - Оценка ваша за урок будет в оценочном листе, который вы мне сейчас сдадите. Сложите все 5 оценок и разделите на 5, это и будет ваша оценка за урок. Ребята, достигли ли Вы своей цели на этом уроке? В оценочном листе подчеркните свой ответ. Рефлексия. В оценочном листе продолжи одно из предложений: (по желанию голос ученика) “Мне понятно… “Я запомнил… “Мне на уроке… “Я думаю…
- Урок закончен. До свидания!
| Ответы учащихся.
|
| Анализ занятия (самоанализ) | Урок цели достиг. Ребятам понравилось обучаться по-новому, они привыкли к работе в группах и малых группах. Учащиеся уже с первого раза понимают, что от них требуется. При составлении вопросов друг к другу обращались по имени, добавляли образные выражения, хотя большинство вопросов были низкого порядка. Составили кластер на тему формулы сокращенного умножения, что показывает развитие критического мышления у учащихся. |
|
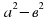 = (а – в)(а + в)
= (а – в)(а + в)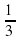 b
b
















