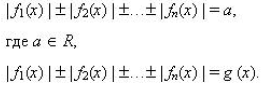Понятие модуля является одной из важнейших характеристик числа в области действительных и комплексных чисел, широко применяется в различных разделах школьного курса математики, физики, но рассмотрение задач, связанных с понятием модуля (а тем более исследование и построение графиков функций, содержащих знак модуля) появляется лишь эпизодически, в рамках изучения той или иной темы. Кроме того, программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях их свойствах, полученных учащимися за период изучения. Тем не менее, задачи, связанные с модулями построением графиков функций, содержащих знак модуля, часто встречаются на математических олимпиадах, вступительных экзаменах в ВУЗы, ЕГЭ. Данный курс позволит учащимся систематизировать, расширить и укрепить знания, связанные с модулем, исследованием и построением графиков функций, подготовиться для дальнейшего изучения тем, использующих эти понятия, научиться решать задачи различной сложности.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Элективный курс по математике "Построение графиков с модулями"
Просмотр содержимого документа
«ЭЛЕКТИВНЫЙ КУРС 11 КЛАСС»
Муниципальное бюджетное общеобразовательное учреждение
«Тюгеевская основная общеобразовательная школа»
Заинского муниципального района Республики Татарстан
«Рассмотрено» «Согласовано» «Утверждаю»
Руководитель ШМО Зам. руководителя по УВР Руководитель МБОУ
«Тюгеевская СОШ»
Назмиева А.Ш._____ Журавлева Н.В.___________ Черяшов А.И.________
Протокол №_______от
«_____»___________2014 г. «_____»__________2014 г. «_____»_________2014 г.
РАБОЧАЯ ПРОГРАММА
элективного курса по математике в 11 классе
«Построение графиков с модулями»
на 2014-2015 учебный год
Учитель: Назмиева Альфия Шарафутдиновна
Категория: первая квалификационная категория
Рассмотрено на заседании
Педагогического совета
Протокол №____________
«______»____________ 2014г.
2014 год
Раздел I. Пояснительная записка
Программа курса на выбор «Построение графиков функций, содержащих знак модуля» адресована учащимся 11 класса.
Понятие модуля является одной из важнейших характеристик числа в области действительных и комплексных чисел, широко применяется в различных разделах школьного курса математики, физики, но рассмотрение задач, связанных с понятием модуля (а тем более исследование и построение графиков функций, содержащих знак модуля) появляется лишь эпизодически, в рамках изучения той или иной темы. Кроме того, программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях их свойствах, полученных учащимися за период изучения. Тем не менее, задачи, связанные с модулями построением графиков функций, содержащих знак модуля, часто встречаются на математических олимпиадах, вступительных экзаменах в ВУЗы, ЕГЭ.
Данный курс позволит учащимся систематизировать, расширить и укрепить знания, связанные с модулем, исследованием и построением графиков функций, подготовиться для дальнейшего изучения тем, использующих эти понятия, научиться решать задачи различной сложности.
Программа курса предполагает знакомство с теорией и практикой рассматриваемого вопроса и рассчитана на 34 часа.
В процессе изучения данного курса предполагается использование различных методов активизации познавательной деятельности учащихся, а также различных форм организации их самостоятельной работы.
Результатом освоения программы является представление учащимися творческих индивидуальных работ на итоговом занятии.
Цели курса:
- обобщение и систематизация знаний по темам модуль, построение графиков функций, содержащих
знак модуля, графическое решение уравнений и неравенств;
- повышение уровня математической подготовки учащихся;
- ориентирование учащихся на выбор математического профиля обучения.
Задачи курса:
- выявить способности учащихся усваивать математику на повышенном уровне;
- способствовать формированию познавательного интереса к математике;
- сформировать навык самостоятельной работы;
- закрепить навыки работы с компьютером;
- сформировать навыки исследовательской работы;
- способствовать развитию алгоритмического мышления учащихся.
Требования к уровню подготовки учащихся.
В результате изучения программы курса по выбору «Построение графиков функций, содержащих знак модуля» учащиеся получают возможность знать и понимать определение модуля действительного числа, правила построения графиков функций, содержащих знак модуля; уметь применять определение, свойства модуля к решению конкретных задач, читать и строить графики функций, содержащих знак модуля, графически решать уравнения и неравенства.
В результате изучения курса учащиеся должны уметь:
точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий;
применять изученные алгоритмы для решения соответствующих заданий;
преобразовывать выражения, содержащие модуль;
решать уравнения и неравенства, содержащие модуль;
строить графики элементарных функций, содержащие модуль.
Раздел II.Система оценки достижений учащихся.
Оценка «отлично»- учащийся демонстрирует сознательное и ответственное отношение, сопровождающееся ярко выраженным интересом к учению; учащийся освоил теоретический материал курса, получил навыки в его применении при решении конкретных задач; в работе над индивидуальными домашними заданиями учащийся продемонстрировал умение работать самостоятельно.
Оценка «хорошо»- учащийся освоил идеи и методы данного курса в такой степени, что может справиться со стандартными заданиями; выполняет домашние задания прилежно (без проявления явных творческих способностей); наблюдаются определенные положительные результаты, свидетельствующие об интеллектуальном росте и о возрастании общих умений учащегося.
Оценка «удовлетворительно»- учащийся освоил наиболее простые идеи и методы курса, что позволило ему достаточно успешно выполнять простые задания.
Раздел III. Учебно – тематический план:
| № | Тема занятия | Количество часов |
| 1 | Вводное занятие. | 1 |
| 2 | Абсолютная величина действительного числа а. | 4 |
| 3 | Правила и алгоритм построения графиков функций, содержащих знак модуля. | 14 |
| 4 | Графическое решение уравнений и неравенств, содержащих знак модуля. | 15 |
| 5 | Всего : | 34 |
1. Вводное занятие ( 1 ч.).
Цели и задачи курса, вопросы, рассматриваемые в курсе, требования, предъявляемые к участникам курса.
Повторение понятия модуля действительного числа, свойства модуля, геометрический смысл модуля.
Практика: решение простейших задач, связанных с понятием модуля.
2. Абсолютная величина действительного числа а. ( 4 ч.).
Основные теоремы. Операции над абсолютными величинами. Упрощение выражений, содержащих переменную под знаком модуля. Применение свойств модуля.
Практика: вычисление выражений, содержащих переменную под знаком модуля с применением свойств модуля.
3. Правила и алгоритм построения графиков функций, содержащих знак модуля ( 14 ч.).
Графики функций вида y = |f(x)|; y = f( |x| ); y = |f( |x| )|; y = |x-a| + |x-b| + |x-c|.
Практика: построение графиков функций вида y = |f(x)|; y = f( |x| ); y = |f( |x| )|;
y = |x-a| + |x-b| + |x-c|.
4. Графическое решение уравнений и неравенств, содержащих знак модуля ( 15 ч.).
Графическое решение уравнений и неравенств, содержащих знак модуля, вида |f(x)| = a; f( |x| ) = a; |f(x)| = |g(x)|; |f(x)| a; f( |x| ) a; |f(x)| |g(x)|.
Практика: решение уравнений и неравенств, содержащих знак модуля, вида |f(x)| = a; f( |x| ) = a; |f(x)| = |g(x)|; |f(x)| a; f( |x| ) a; |f(x)| |g(x)| .
Раздел IV. Используемая литература
1. Егерман, Задачи с модулем. 9-10классы.//Математика.-№23.-2004.-С.18-20.
2. Егерман, Задачи с модулем. 9-10классы.//Математика.-№25-26. -2004.-С.27 -33.
4.Садыкина, Построение графиков и зависимостей, содержащих знак модуля. //Математика. - №33. – 2004. –С.19-21.
5. Скворцова, Уравнения и неравенства с модулем. 8-9классы. //Математика. - №20. -2004.-С.17.
6. Интернет – ресурсы.
Раздел V. Тематическое планирование
| № | Тема урока | Кол-во часов | План | Факт | |
| 1 | Вводное занятие | 1 |
|
| |
|
| Абсолютная величина действительного числа а. | 4 |
|
| |
| 2 | Абсолютная величина действительного числа а. Основные теоремы. | 1 |
|
| |
| 3 | Операции над абсолютными величинами. | 1 |
|
| |
| 4 | Упрощение выражений, содержащих переменную под знаком модуля. | 1 |
|
| |
| 5 | Применение свойств модуля. | 1 |
|
| |
|
| Правила и алгоритм построения графиков функций, содержащих знак модуля. | 14 |
|
| |
| 6 | Основные методы решения уравнений с модулем | 1 |
|
| |
| 7 | График функции 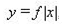| 1 |
|
| |
| 8 | Функция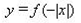 | 1 |
|
| |
| 9 | График функции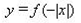 | 1 |
|
| |
| 10 | Функция 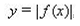| 1 |
|
| |
| 11 | График функции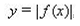 | 1 |
|
| |
| 12 | Функция 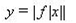| 1 |
|
| |
| 13 | График функции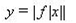 | 1 |
|
| |
| 14 | Функция 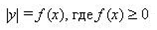| 1 |
|
| |
| 15 | График функции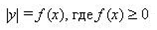 | 1 |
|
| |
| 16 | Функция 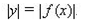| 1 |
|
| |
| 17 | График функции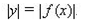 | 1 |
|
| |
| 18 | Графики некоторых простейших функций, заданных явно и неявно, аналитическое выражение которых содержит знак модуля. | 1 |
|
| |
| 19 | Графики уравнений, аналитическое выражение которых содержит знак абсолютной величины. | 1 |
|
| |
|
| Графическое решение уравнений и неравенств, содержащих знак модуля. | 15 |
|
| |
| 20 | Основные методы решения уравнений с модулем | 1 |
|
| |
| 21 | Графическое решение уравнения вида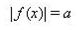 | 1 |
|
| |
| 22 | Уравнение вида 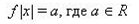| 1 |
|
| |
| 23 | Графическое решение уравнения вида 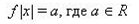| 1 |
|
| |
| 24 | Графическое решение уравнения вида 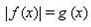| 1 |
|
| |
| 25 | Графическое решение уравнения вида 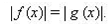| 1 |
|
| |
| 26 | Метод замены переменных при решении уравнений, содержащих абсолютные величины | 1 |
|
| |
| 27 | Метод замены переменных при решении уравнений, содержащих абсолютные величины. Уравнения вида 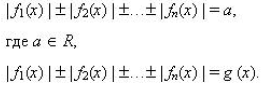| 1 |
|
| |
| 28 | Графическое решение уравнений, содержащих абсолютные величины | 1 |
|
| |
| 29 | Использование свойств абсолютной величины при решении задач | 1 |
|
| |
| 30 | Графическое решение неравенства вида 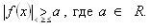| 1 |
|
| |
| 31 | Неравенства вида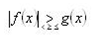 | 1 |
|
| |
| 32 | Графическое решение неравенства вида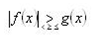 | 1 |
|
| |
| 33 | Неравенства вида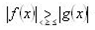 | 1 |
|
| |
| 34 | Графическое решение неравенства вида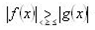 | 1 |
|
| |
|
| Всего | 34 |
|
| |
8
Похожие файлы
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт