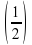СЧАСТЛИВЫЙ
СЛУЧАЙ

ЦЕЛИ И ЗАДАЧИ
- Развивать познавательный интерес;
- Уметь переносить знания в новые условия;
- Формировать эмоционально — ценностное отношение учащихся к предмету, к процессу познания путём разнообразных методов и приёмов;
- Развивать самостоятельность и ответственность ученика за результаты своей деятельности;
- Воспитывать коммуникативные способности учащихся при работе в коллективе.

ХОД ИГРЫ
- Дальше… Дальше… Дальше
- Заморочки из бочки
- Темная лошадка
- Литературная мозаика
- Гонка за лидером

«Дальше… Дальше… Дальше»
Вопросы для первой команды
1
2
3
5
6
4

ВОПРОСЫ ДЛЯ 1 КОМАНДЫ
№ 1
Сколько получится
десятков, если два
десятка умножить
на три десятка?
60
?

ВОПРОСЫ ДЛЯ 1 КОМАНДЫ
№ 2
Делится ли число
111 ∙ 121 ∙ 131 ∙ 141 – 151
на 10?
Да, т.к. оно оканчивается на ноль
?

ВОПРОСЫ ДЛЯ 1 КОМАНДЫ
№ 3
Ряд
Он бывает натуральным.
?

ВОПРОСЫ ДЛЯ 1 КОМАНДЫ
№ 4
Другое название
угломера.
Транспортир
?

ВОПРОСЫ ДЛЯ 1 КОМАНДЫ
№ 5
Метод Эратосфена,
в котором простые числа
«отсеиваются» от
составных?
Решето
?

ВОПРОСЫ ДЛЯ 1 КОМАНДЫ
№ 6
Один отец дал своему сыну, у которого уже была некоторая сумма денег, 2000 руб ., а другой отец своему сыну, у которого не
было денег, 1000 руб . Сразу же после этого сыновья подсчитали, сколько всего у них денег. Оказалось, что всего 2300 руб .
- Как такое могло произойти?
В обмене денег участвовали три человека – «дед», «отец», «сын». «Отец» был «сыном», которому дали 2000 рублей
?

Дальше… Дальше… Дальше
Вопросы для второй команды
1
2
3
5
6
4

ВОПРОСЫ ДЛЯ 2 КОМАНДЫ
№ 1
Назовите число обратное 2.
?

ВОПРОСЫ ДЛЯ 2 КОМАНДЫ
№ 2
Сколько концов
у 3,5 палок?
8
?

ВОПРОСЫ ДЛЯ 2 КОМАНДЫ
№ 3
Место, занимаемое
цифрой в записи числа.
Разряд
?

ВОПРОСЫ ДЛЯ 2 КОМАНДЫ
№ 4
Назовите числа, у которых
столько же цифр, сколько и букв.
100 «сто»,
1000000 «миллион»
?

ВОПРОСЫ ДЛЯ 2 КОМАНДЫ
№ 5
Назовите, пожалуйста, геометрическую фигуру, про которую известно, что если разрезать её определённым образом, то получится известная китайская головоломка
« Танграмм ».
Квадрат
?

ВОПРОСЫ ДЛЯ 2 КОМАНДЫ
№ 6
Что стоит посоветовать
археологам, нашедшим
монету, датированную
35 г. до н.э.?
Ничего. Монета фальшивая. Чеканщики 35 г. до н.э. не могли предполагать о введении нового летоисчисления
?

Заморочки из бочки
3
2
1
4
5
6

Заморочки из бочки
ВОПРОС № 1
Решение:
(2 – 1) + (4 – 3) + (6 – 5) + … +
+(2006 – 2005) = 2006 : 2 = 1003
Вычислите:
(2 + 4 + 6 + … + 2006) – (1 + 3 + 5 + … 2005)
?

Заморочки из бочки
ВОПРОС № 2
Решение:
15 = (11 – 7) + 11. Одновременно перевернём часы, через семь минут начинаем варить кашу. После четырех минут (песок в часах за 11 минут закончится) вновь перевернём часы на 11 минут.
Имеются двое песочных часов:
на 7 минут и на 11 минут .
Каша должна вариться 15 минут .
Как сварить её, перевернув часы
минимальное количество раз?
?

Заморочки из бочки
ВОПРОС № 3
Так как на седьмом озере сели оставшиеся гуси и больше не осталось, то там сел один гусь. Если бы прилетело 2 гуся, то 1 гусь бы остался.
7 озеро: 1 гусь;
6 озеро: (гуся)
5 озеро: (гусей)
4 озеро: (гусей)
3 озеро: (гусь)
2 озеро: (гуся)
1 озеро: (гусей)
Над озёрами летели гуси. На каждом озере садилась половина гусей и ещё полгуся, остальные летели дальше. Все сели на семи озерах. Сколько было гусей?
?

Заморочки из бочки
ВОПРОС № 4
Решение:
Так ка сын родился тогда, когда отцу было 25 лет, то разница в возрасте 25 лет. Тогда:
65 – 25 = 40(лет)–удвоенный возраст сына;
40 : 2 = 20 (лет) – сыну;
20 + 25 = 45 (лет) – отцу.
Отцу и сыну вместе 65 лет.
Сын родился, когда отцу было 25 лет.
Какого возраста отец и сын?
?
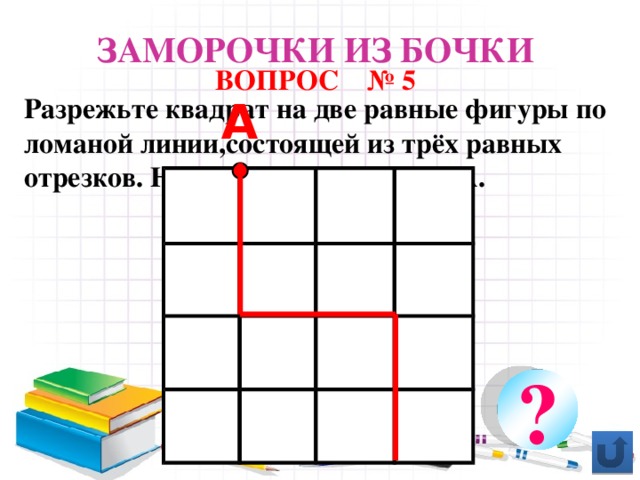
Заморочки из бочки
ВОПРОС № 5
Разрежьте квадрат на две равные фигуры по ломаной линии,состоящей из трёх равных отрезков. Начало разреза в точке А.
А
А
?

Заморочки из бочки
ВОПРОС № 6
Математик, оказавшись в небольшом городке, решил
подстричься. В городке было всего лишь две
парикмахерских. Заглянув к одному мастеру, он увидел,
что в салоне грязно, сам мастер одет неряшливо, плохо
выбрит и небрежно подстрижен. В салоне второго
мастера было чисто, а сам владелец был
безукоризненно одет, чисто выбрит и аккуратно
подстрижен. Тем не менее, математик отправился
стричься к первому парикмахеру. Почему?
Решение:
Так как в городе только две парикмахерских, а второй хорошо выбрит и подстрижен, то подстриг его первый мастер.
?

Темная лошадка
Пифагор
Самосский
Задание № 1
Задание № 2
?

Темная лошадка
Задание № 1
Решение: Рассмотрим два случая.
- Пусть А говорит правду, тогда В – лжец. Так как В – лжец, то В и С не из одного города, поэтому С – честный человек.
- Пусть А – лжец, тогда В говорит правду. Следовательно, В и С из одного города, поэтому С – честный человек.
На острове два города. В одном живут честные люди, говорящие только правду, а в другом – лжецы. Встретились три человека А , В и С . А говорит: « В – лжец ». В говорит: « Я и С из одного города». Кто такой С ?
?

Темная лошадка
Задание № 2
В этом зашифрованном примере одинаковым фигурам соответствуют одинаковые цифры. Расшифруйте пример. Подсказка: чаще всего встречается цифра 5.
535
345
880
Ответ:
+
⁺
?

Литературная мозаика
I этап. «РУССКИЕ ПОСЛОВИЦЫ»
II этап. «МУЗЫКАЛЬНАЯ ПАУЗА»
III этап. «КИНОФЕСТИВАЛЬ»

Литературная мозаика
I этап. «РУССКИЕ ПОСЛОВИЦЫ»
Назовите русские пословицы, поговорки, афоризмы, где фигурируют числа. Вы должны использовать натуральные числа подряд в порядке возрастания.

Литературная мозаика
II этап. «МУЗЫКАЛЬНАЯ ПАУЗА»
Спойте строчки из песен, где
фигурируют числа.

Литературная мозаика
III этап. «КИНОФЕСТИВАЛЬ»
Вспомните названия фильмов,
где фигурируют числа.

Гонка за лидером

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ
5
4
3
6
2
1
9
10
11
12
7
8
16
17
14
13
18
15

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 1
5
Высший балл в школах России.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 2
вектор
Направленный отрезок.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 3
1 см
Одна сотая метра.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 4
Геометрия, в которой изучаются фигуры на плоскости.
планиметрия
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 5
многочлен
Сумма одночленов.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 6
33
Сколько лет спал Илья Муромец.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 7
2
Наименьшее четное число.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 8
180°
Сумма углов треугольника.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 9
Геометрическая фигура в любовных делах.
треугольник
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 10
Параллелограмм, у которого все стороны равны.
ромб
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 11
Что является графиком функции ?
гипербола
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 12
Треугольник, у которого есть прямой угол.
прямоугольный
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 13
синус
Отношение противолежащего катета к гипотенузе.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 14
правильная
Дробь, у которого числитель меньше, чем знаменатель.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 15
Отрезок, соединяющий точку окружности с центром.
радиус
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 16
Масса кубического метра воды.
килограмм
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 17
крестик
Соперник нолика.
?

Гонка за лидером
ВОПРОСЫ ПЕРВОЙ КОМАНДЕ. № 18
Фигура, состоящая из точек и последовательно соединяющих их отрезков.
ломаная
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ
5
4
3
6
2
1
9
10
11
12
7
8
16
17
14
13
18
15

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 1
Очень плохая оценка знаний.
2
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 2
Простейшая линия в геометрии.
прямая
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 3
Сколько козлят было у многодетной козы?
7
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 4
Наука о свойствах геометрических фигур.
геометрия
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 5
уравнение
Равенство с переменной.
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 6
Сколько музыкантов в квартете?
4
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 7
Наименьшее натуральное число.
1
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 8
процент
Сотая часть числа.
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 9
косынка
Треугольный платок.
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 10
Параллелограмм, у которого все углы прямые.
прямоугольник
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 11
Сколько пьес во «Временах года» Чайковского?
12
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 12
Что является графиком функции y = kx + b .
прямая
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 13
Треугольник, у которого все стороны равны.
равносторонний
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 14
Отношение противолежащего катета к прилежащему.
тангенс
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 15
Уравнения, имеющие одни и те же корни.
равносильные
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 16
Объем килограмма воды.
литр
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 17
Часть прямой.
отрезок
?

Гонка за лидером
ВОПРОСЫ ВТОРОЙ КОМАНДЕ. № 18
Сумма всех сторон
п - угольника.
периметр
?

ВАШЕ НАСТРОЕНИЕ
ПОСЛЕ ИГЫ…

ВСЕМ СПАСИБО.
СЧАСТЬЯ, ЛЮБВИ
И ПРОЦВЕТАНИЯ!
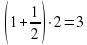 (гуся)
(гуся)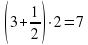 (гусей)
(гусей)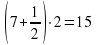 (гусей)
(гусей)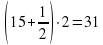 (гусь)
(гусь)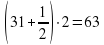 (гуся)
(гуся)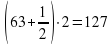 (гусей)
(гусей)
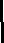








 А
А 


 +
+