МАТЕМАТИЧЕСКАЯ ВИКТОРИНА
( 7 класс).
Математическая викторина – это особый вид игры, которая ставит своей целью выявить учащихся с наибольшим общим математическим развитием, их начитанность и умение быстро ориентироваться в решении несложных математических вопросов.
Ход викторины:
Баллада о математике
Как воздух,
Математика Нужна,
Одной отваги
Офицеру мало.
Расчёты! Залп!
И цель поражена
Могучими
Ударами
Метала
И воину
Припомнилось на миг,
Как школьником
Мечтал в часы учения
О подвиге,
Шквалах огневых,
О яростном
Порыве наступления.
НО строг учитель был,
И каждый раз
Он обрывал мальчишку
Резковато:
«Мечтать довольно!
Повтори рассказ
О свойствах круга
И углов квадрата!»
И воином
Любовь сбережена
К учителю,
Далёкому, седому.
Как воздух,
Математика нужна,
Сегодня.
Офицеру молодому.
(М. Барзаковский.)
2) Вопросы:
1. Что принимают за единицу длины? (метр)
2. Сколько см³ в 1м³? (1000)
3. Скажите точно продолжительность 1 года? (365-366)
4. Сколько в году недель? (52)
5. Всякая ли теорема имеет для себя обратную теорему? (Нет)
6. Скажите признак делимости на 3 и 9? (99=9+9=18:9, и на 3)
7. Вычисли в уме 25²–4 (621)
8. Что больше а или 2а? (a<2a, если a>0 ; a>2a, если а<0)
9. Что больше а или а² ? (a<a² при любом а)
10. 12 человек обменялись рукопожатиями, сколько было рукопожатий? (12:2=6)
11. Что такое решето Эратосфена? (простые числа)
12. Подсчитайте (устно) сумму всех чисел от 1 до 100 (5050)
13. Каким числом является нуль: чётным или нечётным? (нейтральное число)
О нуле:
Когда-то многие считали,
Что нуль не значит ничего.
И, как ни странно, полагали,
Что нуль совсем не есть число.
Но на оси средь прочих чисел
Он всё же место получил,
И все действительные числа
На два разряда разделил.
Нуль ни в один из них не входит,
Он сам составил чисел класс,
О всех его особых свойствах
Мы поведём сейчас рассказ.
Коль нуль к числу ты прибавляешь
Иль отнимаешь от него,
В ответе тотчас получаешь
Опять то самое число.
Попав как множитель средь чисел,
Он сводит мигом всех на нет.
И поэтому в произведение
Один за всех несёт ответ.
А относительно деления,
Во – первых, нужно помнить то,
Что уж давно в научном мире
Делить на нуль запрещено.
Причина всем ведь очевидна,
А состоит причина в том,
Что смысла нет в таком деленье,
Противоречие в нём самом.
И впрямь: какое из известных
Число за частное нам взять,
Когда с нулём в произведенье
Все числа нуль лишь могут дать?
14. Может ли сумма двух слагаемых быть меньше каждого из слагаемых быть меньше каждого из слагаемых? (может, сумма «+» и «-» числа)
15. Напишите римскими цифрами 1947.
16. Какой стол устойчивее – на трёх или четырёх ножках и почему? (На трёх)
17 Назовите то число, которое делится без остатка на любое число? (1)
18. Как с помощью трёх двоек написать наибольшее число? (2²²)
19. Проведите прямую линию так, чтобы она пересекала все стороны треугольника SHAPE \* MERGEFORMAT
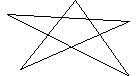
20. Сколько треугольников в фигуре? (10)
SHAPE \* MERGEFORMAT
21. Узнать число, месяц и год рождения.
Взять листки и ручку.
«Я могу узнать совершенно точно, когда каждый из вас родился. Для этого попрошу сделать ряд вычислений, которые вы должны выполнить не торопясь, правильно. Слушайте внимательно и делайте.
Порядковый номер месяца вашего месяца рождения умножьте на 100. к полученному произведению прибавьте число месяца. Теперь полученную сумму умножьте на 2 и к новому произведению прибавьте 8. новую сумму надо умножить на 5 и к полученному произведению прибавить 4. умножьте опять полученную сумму на 10 и опять прибавьте 4. затем прибавьте полное число ваших лет».
Каждого из вычисляющихся вы просите окончательный результат написать на доске. Допустим, в ваших примерах это будут числа 101676 и 50964. В уме отнимаете от написанного числа всегда 444 и остаток разбить справа налево на группы по две цифры в каждом.
101676 50964
- ___444 - ___444
10.12.32. 5.05.20.
Последние две цифры показывают полное число лет; вторая группа – число месяца, а первая группа – порядковый номер месяца.
Если обозначить порядковый месяца буквой а, число месяца – b, а число полных лет – с, то все производимые выше вычисления будут выражены следующей формулой:
{[ (100а + b) 2 + 8 ] * 5 + 4} * 100 + 4 + с = 10000а + 100b + 444 + с, но 444 отняли, тогда 10000а + 100b + с.
22. задача с яблоками.
Нам с Гомеля тётя
Ящик яблок прислала.
В этом ящике яблок
Было в общем немало.
Начала эти яблоки
Спозаранок считать я.
Помогали мне сёстры,
Помогали мне братья.
И пока мы считали,
Мы ужасно устали,
Мы устали, присели
И по яблоку съели.
И осталось их – сколько?
А осталось их столько,
Что пока мы считали
Восемь раз отдыхали.
Восемь раз отдыхали,
Восемь раз мы сидели.
И по яблоку съели.
И осталось их – сколько?
Ох, осталось их столько
Что когда этот ящик
Мы опять поглядели,
Там на дне его чистом
Только стружки белели…
Только стружки – пеструшки.
Только стружки белели.
Вот прошу угадать я.
Всех ребят и девчонок:
Сколько было нас, братьев?
Сколько было сестрёнок?
Поделили мы яблоки
Все без остатка.
А всего-то их было
Пятьдесят без остатка. (л. Пантелеев)
(3 брата и 2 сестры)
Итоги:
Ученики, которые ответили полно на 5-6 вопросов ставим оценку – «5», на 4 вопроса – «4», на 3 вопроса – «3».