После изготовления первого компьютера стало ясно, что при его производстве возможно использование только цифровых технологий – ограничение сигналов связи единицей и нулём для большей надёжности и простоты архитектуры персонального компьютера. Благодаря своей бинарной природе, математическая логика получила широкое распространение в ВТ и информатике. Были созданы электронные эквиваленты логических функций, что позволило применять методы упрощения булевых выражений к упрощению электрической схемы. Кроме того, благодаря возможности нахождения исходной функции по таблице позволило сократить время поиска необходимой логической схемы. В программировании логика незаменима как строгий язык и служит для описания сложных утверждений, значение которых может определить компьютер.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
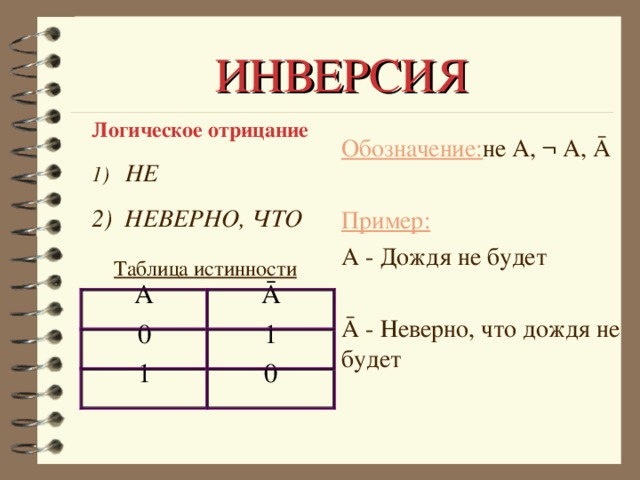
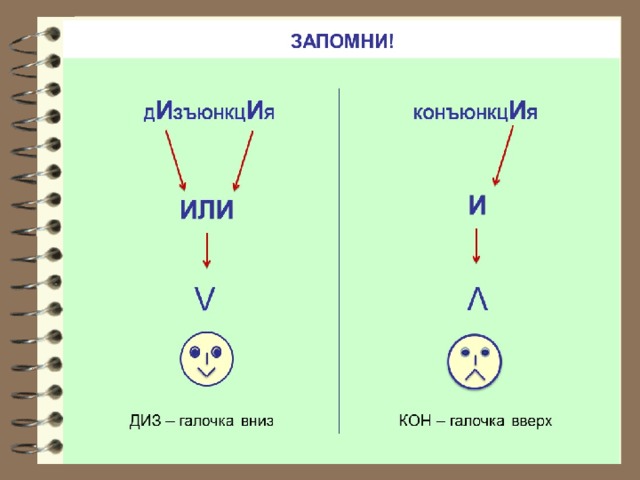
Основные понятия алгебры логики
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Основные понятия алгебры логики»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2420 руб.
2200 руб.
3140 руб.
1670 руб.
2380 руб.
2200 руб.
3140 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства