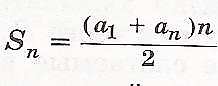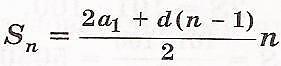| Вопросы: дайте определение арифметической прогрессии; напишите формулу n-го члена арифметической прогрессии; назовите свойство членов арифметической прогрессии. Задания для устной работы: Последовательность уn задана формулой n-го члена: уn = 5n + 1. Найдите у1, у4, у20, у100. Последовательность задана формулой аn = 15 - 3n. Найдите номер члена последовательности, равного 0; -3. Зная, первые два члена арифметической прогрессии 3; -2; …, найдите следующие за ними четыре ее члена.
(уn): 3; 7; … - арифметическая прогрессия. Найдите: 1). d. 2). а17. 3). Составьте формулу n-го члена арифметической прогрессии. | Ученики отвечают на вопросы.
Ответы: у1 = 5 • 1 + 1 = 6; у4 = 5 • 4 + 1 = 21; у20 = 5 • 20 + 1 = 101; у100 = 5 • 100 + 1 = 501. 0 = 15 - 3n; -3 = 15 - 3n; 3n = 15; 3n = 18; n = 5. n= 6.
d = -2 -3 = -5; а3 = -2 + (-5) = -7; а4 = -7 + (-5) = -12; а5 = -12 + (-5) = -17; а6 = -17 + (-5) = -22. 4. 1). d = 7 – 3 = 4; 2). а17 = 3 + 4(17 – 1) = 68; 3). аn = 3 + 4(n – 1); аn = 4n – 1. Регулятивные, коммуникативные УУД |
| Классу предлагается решить несколько занимательных задач. Можно ли циферблат часов разделить на 6 частей так, чтобы в каждой части находилось по два числа, причем суммы этих двух чисел в каждой из шести частей были бы равны между собой?

Не прибегая к последовательному сложению, сосчитать, сколько очков на всех десяти косточках домино. 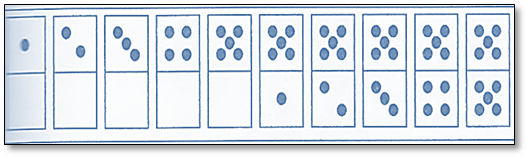
А теперь рассмотрим арифметическую прогрессию, представляющую собой ряд натуральных чисел, и найдем сумму ста первых ее членов.
Совет мудреца Задача очень не проста: Как сделать, чтобы быстро От единицы и до ста Сложить в уме все числа? Давным-давно один мудрец Сказал, что прежде надо Связать начало и конец У численного ряда. Пять первых связок изучи, Найдешь к решению ключи!
Замечание. Сначала открывается первое четверостишье. Если учащиеся ответ не дадут, то учитель открывает подсказку – остальную часть стихотворения. Сколько таких пар? Как вычислить сумму? Рассказать учащимся о маленьком Карле Гауссе, который решил эту задачу, будучи 10-летним учеником.
Когда учитель предложил ученикам третьего класса сложить все числа от 1 до 100 включительно, рассчитывая при этом надолго занять их работой, маленький Карл моментально подошел с готовым ответом. Возможно, он заметил, что каждая из сумм 1 + 100, 2 + 99, 3 + 98, … равна 101, а таких сумм 50.
| Предлагают различные варианты решения. Верный ход решения. а). Сумма всех чисел, обозначенная на циферблате равна 78, т.е. 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 +11 + 12 = 78. б). А так как нам нужно циферблат разделить на 6 частей, то получаем 78 : 6 = 13. 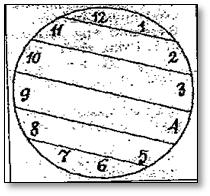
Ответ. Циферблат можно разделить на 6 равных частей.
а). Приходим к необходимости вычислить сумму 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10. б). Образуем пары чисел, которые нужно сложить: 1 и 10, 2 и 9, 3 и 8, 4 и 7, 5 и 6. в). Сумма очков в каждой паре равна 11, а таких пар пять, находим 11• 5 = 55. 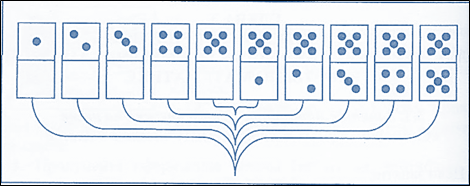
Ответ. 55.
Регулятивные, познавательные УУД

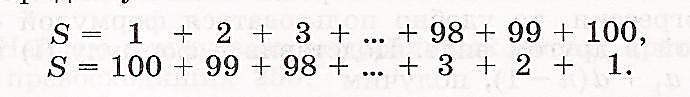
Учащиеся предлагают сложить пары чисел 1 и 100, 2 и 99, 3 и 98 и т.д., замечают, что сумма одинаковая.
Ответ. 50. Ответ. Сумма равна 101 • 50 = 5050. У
чащиеся рассказывают исторические сведения о том, что многочисленные исследования К. Гаусса в области алгебры, теории чисел и математического анализа оказали значительное влияние на развитие теоретической и прикладной математики, астрономии, физики. Личностные, познавательные УУД |
| С помощью рассуждений, аналогичных тем, которые мы провели при вычислении суммы первых ста натуральных чисел, можно найти сумму первых n членов любой арифметической прогрессии. Что получится, если в формулу вместо аn подставить формулу n-го члена арифметической прогрессии? Замечание. При вычислении суммы первых n членов арифметической прогрессии учащиеся могут использовать ту из двух формул, применение которой в каждом конкретном случае более целесообразно. | Путем рассуждений учащиеся выводят формулу, учитывая то, что сумма членов арифметической прогрессии, равностоящих от ее концов, есть величина постоянная. 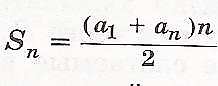
Ответ. Еще одна формула для вычисления суммы первых n членов любой арифметической прогрессии. 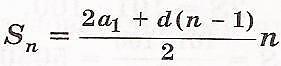
Регулятивные, познавательные УУД |
| В процессе первичного закрепления примеры решаются с комментированием. В ходе работы учитель оказывает помощь учащимся класса.
№ 610. Найдите сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно, если первый член 10 и разность равна 3.
№ 616. Шары расположены в форме треугольника так, что в первом ряду 1 шар, во втором – 2, в третьем – 3 и т.д. Во сколько рядов размещены шары, если их число равно 120? | Учащиеся записывают решение в тетрадях.
Решение. а15 = 10 + 14•3 = 52, а30 = 10 + 29•3 = 97. Найдем номер последнего члена этой прогрессии: 97 = 52 + (n-1) • 3, n = 16 S16 = (52 + 97) • 16 : 2 = 1192. Ответ. 1192.
Решение. Так как количество шаров в ряду равно номеру ряда, составим последовательность: 1; 2; 3; …; n. Тогда количество всех шаров, размещенных в n рядах – это сумма первых n членов арифметической прогрессии. Sn = (1 + n) • n: 2, Sn = 120. Решая уравнение n2 + n – 240 = 0, получим n = 15. Ответ. 15.
Регулятивные УУД
|
| Учитель разъясняет выполнение домашнего задания. Заполните таблицу, где (аn) - арифметическая прогрессия. а1 – первый член арифметической прогрессии, аn – n-ый член арифметической прогрессии, n – число ее членов, Sn – сумма первых n членов арифметической прогрессии, d – разность прогрессии.
| а1 | d | n | аn | Sn | | 8 |
| 33 |
| 1848 | | 14 | 5 |
|
| 26150 | | 4 | 3 | 33 |
|
| | 5 | -7 |
|
| -1656 | | 84 | -4 |
|
|
|
| Учащиеся выполняют работу в тетрадях.
Ответ.
| а1 | d | n | аn | Sn | | 8 | 3 | 33 | 104 | 1848 | | 14 | 5 | 100 | 509 | 26150 | | 4 | 3 | 33 | 100 | 1716 | | 5 | -7 | 23 | -149 | -1656 | | 84 | -4 | 25 | -12 | 900 |
|
| Учитель подводит итог урока, оценивает работу учащихся, выставляет отметки, комментируя их, просит каждого ученика нарисовать смайлик соответствующий его эмоциональному состоянию.
Вопросы: какую задачу ставили? Удалось решить поставленную задачу? Каким способом? Какие получили результаты? Где можно применить новые знания? | Оцени себя сам   На уроке немного затруднялся, не все понятно. На уроке было трудно, ничего не понял. На уроке было комфортно и все понятно 
|