Разработка урока алгебры по теме «ФОРМУЛЫ n ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ»

Конспект урока по теме

«ФОРМУЛЫ n ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ»

Слайд 1

I . ОРГАНИЗАЦИОННЫЙ ЭТАП.

Здравствуйте, садитесь. Откройте тетради. Запишите число, классная работа.

Сегодня на уроке мы продолжим изучать один из увлекательнейших разделов алгебры «Прогрессии»

Термин «прогрессия» имеет латинское происхождение. Термин «progression» был введен римским философом и математиком Боэцием (VI в.). Как вы думаете, что означает это слово?

- «движение вперед», «успех» (на экране-«движение вперед», «успех»)

Не будем останавливаться и мы, а пойдем вперед в направлении изучения прогрессий.

Слайд 2

Как сказал Леонид Андреев: «Чтобы идти вперед, чаще оглядывайтесь назад, ибо вы забудете, откуда вы вышли и куда вам нужно идти». Давайте оглянемся , что на данный момент мы знаем о прогрессиях.

-Как называется прогрессия, которую мы изучаем?

(арифметическая).

Что мы о ней знаем, выясним в ходе устной работы

(один ученик решает тест-онлайн на ноутбуке)

II . ЭТАП АКТУАЛИЗАЦИИ ЗНАНИЙ.

Слайд 3

Являются ли арифметическими прогрессиями последовательности чисел:

3, 7, 12, … Ответ: нет, 7-3=4, 12-7=5

28, 31,34… Ответ: да, Ответ: d=3

Дайте определение арифметической прогрессии. Запишите это определение с помощью формулы в справочник на доске и в тетради Ответ: a_n+1 = a_n + d

Как называется каждый компонент этой формулы? Ответ: a_n+1 – последующий член, a_n-предыдущий член прогрессии, d – разность.

Как найти разность арифметической прогрессии. Запишите формулу в справочник и тетради. Ответ: d = a_n+1 – a_n

Найдите разность арифметической прогрессий: 28, 31,… Ответ: d=3

Слайд 4

Скажите, а какой еще формулой можно задать арифметическую прогрессию? Запишите эту формулу? Ответ: a_n=kn+b.

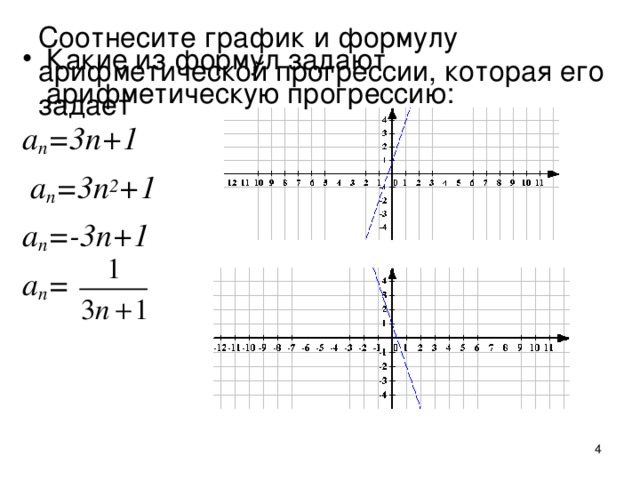
Какие из формул задают арифметическую прогрессию: a_n=3n+1, a_n=3n²+1, a_n=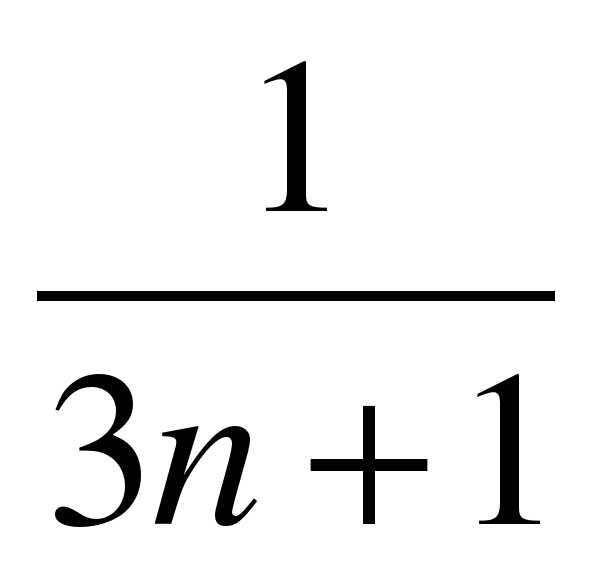,a_n=-3n+1? Ответ: a_n=3n+1, a_n=-3n+1

Соотнесите график и формулу арифметической прогрессии, которая его задает a_n=3n+1, a_n=-3n+1. Объясните свой выбор. Найдите разность каждой прогрессии.

Ответ: 3, -3.

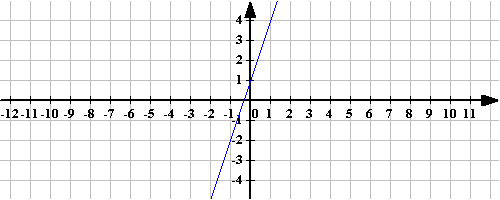
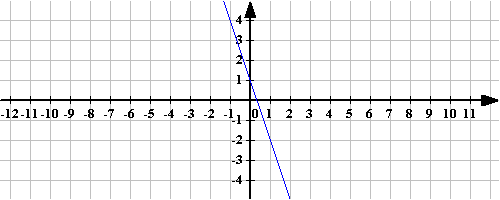
Итак, линейная функция является арифметической прогрессией. Дома, решая № 598, вы должны были доказать, что последовательность сумм внутренних углов треугольника, выпуклого четырехугольника, выпуклого пятиугольника и т.д. является арифметической прогрессий.

Один ученик объясняет решение этого задания. (решение записано на доске заранее)

Слайд 5

Продолжите арифметическую прогрессию: 28, 31,34… Ответ: 37,40,43…

Всегда ли удобен такой способ нахождения неизвестных членов прогрессии?

Чем удобнее воспользоваться?

Запишите формулу n-го члена арифметической прогрессии.

Ответ: a_n = a₁ + (n – 1) ∙ d

Что означает буква n?

Найдите одиннадцатый член этой прогрессии: Ответ: 58

III. ЭТАП ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА И ЗАКРЕПЛЕНИЕ ЗНАНИЙ В СТАНДАРТНОЙ СИТУАЦИИ.

Слайд 6

(1,2,3…100. Портрет К. Гаусса)

Продолжите последовательность 1,2,3,…..

Скажите, сколько времени вам понадобится для того, чтобы сложить, к примеру, все натуральные числа от 1 до 100?

Совершенно не сомневаюсь в ваших способностях. Истории математики известны случаи очень раннего проявления математических способностей.

(ученик выступает с сообщением о юном Гауссе)

Очень рано раскрылись дарования и у Карла Гаусса, позднее ставшего одним из крупнейших математиков XIX ве­ка (его даже называли «царем математиков»).

Рассказывают, что в возрасте трех лет он заметил ошибку, сделанную его отцом в расчетах. А семи лет мальчик пошел в школу. В то время в одной классной комнате занимались уче­ники разных классов. Чтобы занять первоклассников, пока он будет заниматься с третьим классом, учитель велел им сло­жить все числа от 1 до 100. Но не успел он закончить чтение условия задачи, как маленький Карл написал на своей гри­фельной доске ответ и положил на учительский стол.

С сожалением смотрел преподаватель на мальчика: ясно было, что за такой короткий срок он не мог сделать 99 сложе­ний. Остальные ученики терпеливо складывали числа, сби­ваясь, стирая написанное и снова складывали. Когда учитель закончил занятия с третьеклассниками, он взял со своего стола грифельные доски. Ни у кого не было правильного резуль­тата. И только на доске Карла стоял ответ: 5050, причем ни­каких вычислений- не было.

«Как же ты это сосчитал?» — спросил учитель.

«Очень просто,— ответил мальчик.— Я сложил 1 и 100, получил 101. Потом сложил 2 и 99, тоже получилось 101; 3 и 98— снова 101, и так до 50+51=101. Значит, надо сло­жить 50 слагаемых по 101 каждое, то есть умножить 101 на 50. А это и равно 5050».

Изумленный учитель понял, что встретил самого способного ученика в своей жизни. В дальнейшем Гаусс сделал много замечательных открытий в математике.

Юный Гаусс сам того, не подозревая, вывел формул первых 100 членов арифметической прогрессии.

На этом уроке, подобно Гауссу, мы выведем в общем виде формулы суммы n-первых членов арифметической прогрессии и рассмотрим некоторое их применение к практическим задачам.

Слайд 7 (тема урока)

Запишите в тетради тему урока «Формулы суммы n-первых членов арифметической прогрессии»

Слайд 8. (условие задачи, дано)

Сумму п первых членов арифметической прогрессии принято обозначать как S_n.. Вывод формулы проведем в ходе решения задачи «Найти сумму п первых членов арифметической прогрессии, если известны ее первый и n-ый члены.»

Дано:

(a_n)- арифметическая прогрессия

a_1, a_n

S_n-?

Вывод: Найдем суммы a₁+ a_{n ,} a₂+ a_n-1= (a₁+ d)+(a_n- d )= a₁+ a_n, очевидно, что a₃+ a_n-2 =a₁+ a_n и т.д. Таких пар будет n/2. значит, S_n= (a₁+ a_n)• n/2, т. е.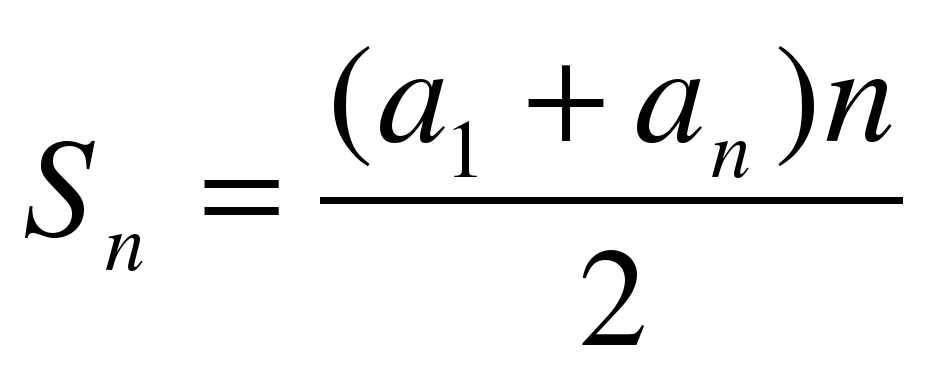

Обращаю ваше внимание, что в учебнике приведен другой вывод этой формулы, с ним вы ознакомитесь дома.

С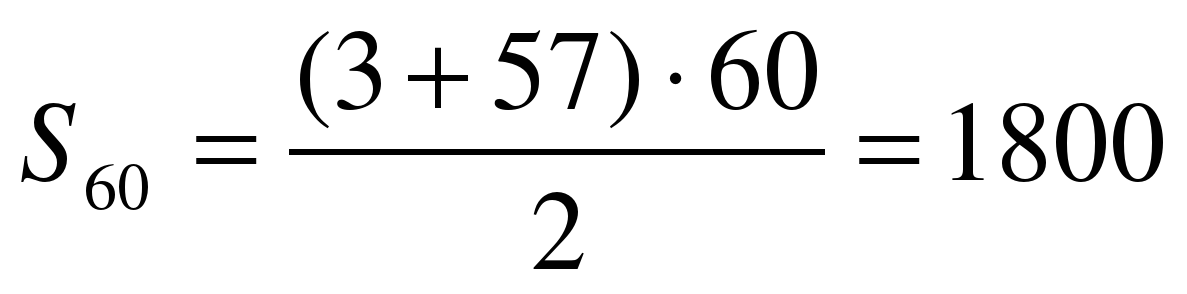лайд 9 Используя формулы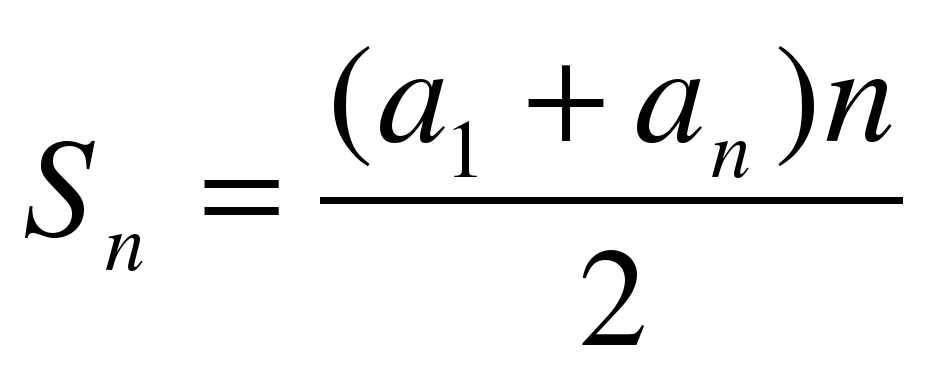решите № 603а стр.151Сверим решение :

Решите №605(а) стр.151. Удобно ли применить формулу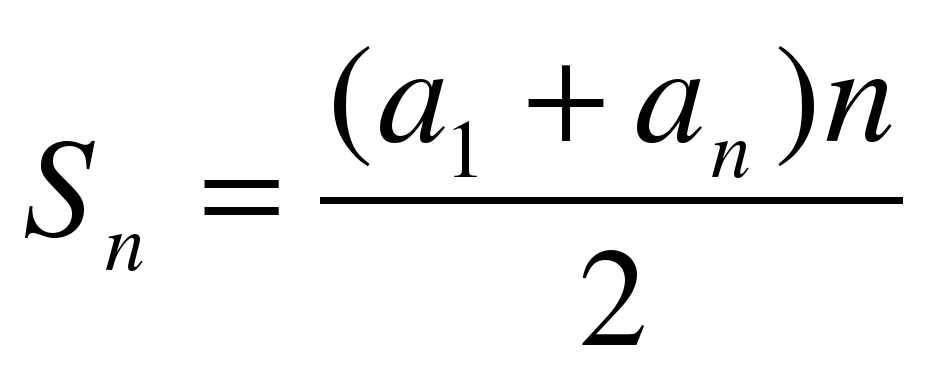, применительно к данной задаче? Что из условия известно? Ваши предложения по решению?

Выведем в общем виде вторую формулу суммы n-первых членов арифметической прогрессии, если известны a₁ и d. (ученик выводит формулу на доске)

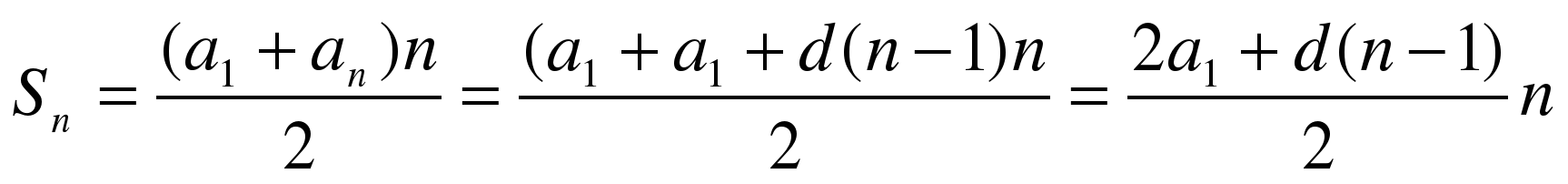. Итак,

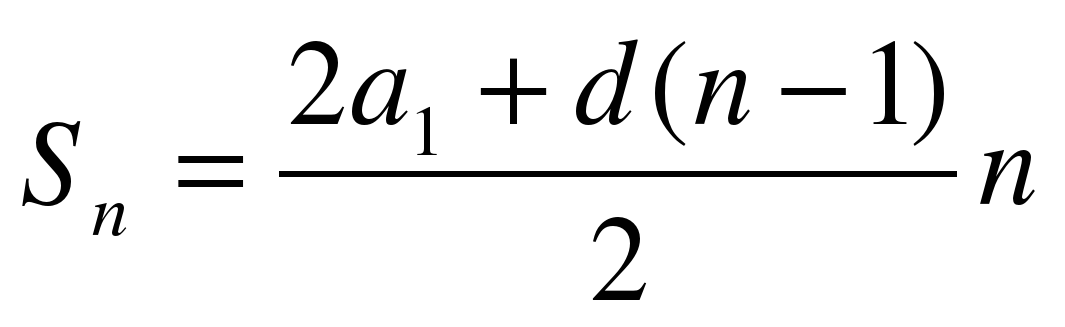. Используя эту формулу решите задачу. Сверим решение: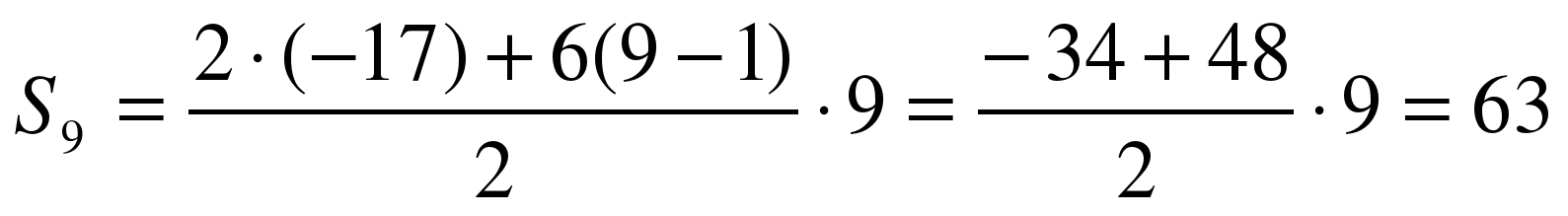

IV МИНУТКА ОТДЫХА.

Слайд 10.

Формулы вывели. Прогресс заметен. Можно чуточку и отдохнуть. А для математиков лучший отдых – порешать задачки и покрутить головоломки.

Ученик объясняет условие: На экране записано 20 чисел: 1,4,7,10,13,16,19,22,25,28,31,34,37,40,43,46,49,52,55,58.

Я не буду на них смотреть. Назовите номер числа, и я мгновенно назову это число. (2-3 числа) Можете объяснить, как мне это удается? (выслушивает версии) Прогрессия здесь задана формулой a_n=3n-2. Мне остается подставить в формулу номер и посчитать.

V ЭТАП ЗАКРЕПЛЕНИЯ ЗНАНИЙ В НЕСТАНДАРТНОЙ СИТУАЦИИ.

Мы движемся вперед.

Слайд 11. задача от строителя

Рассмотрим некоторое применение формул к практическим задачам.

Начнем со строительства. Прочитайте условие задачи и переведите его на язык математики:

Вертикальные стержни конструкции имеют следующую длину: наименьший 5 дм, а каждый следующий на 2 дм длиннее. Найдите длину семи таких стержней.

(один человек у доски) Ответ:77 дм

Слайд 12.

Следующая задача связана с физикой. № 614 стр. 152

Прочитайте условие задачи и переведите его на язык математики.

(один человек у доски) Ответ125м

Слайд 13

2015год юбилейный год для нашего поселка. Ровно 105 лет назад, в 1910 году на берег реки Туртас высадились первые переселенцы из Вятской губернии. Так появился на карте поселок Чебунтан. Новый этап жизни поселок начал в связи с лесоразработками и открытием в 1973 году лесозаготовительного объединения «Туртаслес». Поселок лесозаготовителей переименовали в Туртас. Сейчас лесная промышленность переживает не самые лучшие времена, но по-прежнему многие туртасцы остаются преданными лесной промышленности. Предлагаю вам рассмотреть следующую задачу. ( решение демонстрирует ученик, получивший это индивидуальное задание)

При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основание положить 12 бревен?

Слайд 13 Ответ: 78 бревен в одной кладке.

VI ЭТАП. ПРОВЕРКИ УСВОЕНИЯ ЗНАНИЙ

Как видим, арифметическая прогрессия вокруг нас. Есть она и в заданиях государственной итоговой аттестации. А значит, эти формулы нужно знать и уметь применять. Чтобы определить, как вы разобрались в применении формул, предлагаю вам решить небольшой тест. Тот, кто решит тест, на доске напишите свои ответы.

Вариант 1.

1. Из предложенных последовательностей выберите ту, которая может являться арифметической прогрессией:

1) 1; 11; 21; 31… 2) 1; 2; 4; 9; 16…

3) 2; 4; 8; 16… 4) 7; 8; 7; 8…

2. Перед вами четыре числа. Какое из этих чисел является шестым членом последовательности натуральных чисел, кратных 5:

1) 25; 2) 30; 3) 40; 4) 35?

3. Чему равна сумма пяти первых членов арифметической прогрессии, если а₁=3, а₅= 25

1) 65 , 2) 80 , 3) 70, 4) 75

4. Последовательность 4; -6… является арифметической прогрессией. Какое из предложенных чисел будет равно сумме восьми первых ее членов?

1) 312; 2) -24; 3) 77; 4) -248.

Вариант 2.

1. Из предложенных последовательностей выберите ту, которая может являться арифметической прогрессией:

1) 2; 7; 12; 17… 2) 1; 2; 4; 9; 16…

3) 2; 4; 8; 16… 4) 7; 8; 7; 8…

2. Перед вами четыре числа. Какое из этих чисел является шестым членом последовательности натуральных чисел, кратных 3:

1) 24; 2) 18; 3) 21; 4) 12?

3. Чему равна сумма пяти первых членов арифметической прогрессии, если а₁=2, а₅= 28

1) 65 , 2) 80 , 3) 75, 4) 70

4. Последовательность 2; -4… является арифметической прогрессией. Какое из предложенных чисел будет равно сумме восьми первых ее членов?

1) 312; 2) -42; 3) -312; 4) -152.

( Верный ответ 1;2;3;4 – возрастающая арифметическая прогрессия)

Слайд 17 VII ЭТАП ОБЪЯСНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ

Возрастающая прогрессия символизирует прогресс, движение вперед. Если же вернуться к истокам, то можно узнать, что первые представления об арифметической прогрессии были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания, как их решать.

В древнеегипетском папирусе Ахмеса (ок. 2000 лет. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.» В этой задаче речь идет об арифметической прогрессии.

Приготовить решение этой задачи к следующему уроку предлагается учащимся, проявляющим интерес к математике, ученику, интересующемуся историей в Интернете или энциклопедиях найти историческую справку об этом папирусе.

Для остальных домашнее задание : п.26 выучить формулы № 604, №607, на повторение № 619

ИТОГ УРОКА, выставление, комментирование оценок за работу на уроке.

А урок закончу словами царя математиков Карла Гаусса: «Математика – царица наук, а арифметика – царица математики». Любите математику, учите математику, и тогда вам любая наука будет по плечу. Знайте: ничто не дисциплинирует человека, так, как математика, ничто не развивает его способности, так как математика, и ничто не ведет вперед к успеху так, как математика. Успеха и постоянного движения вперед! Урок закончен.

Очень рано раскрылись дарования и у Карла Гаусса, позднее ставшего одним из крупнейших математиков XIX ве­ка (его даже называли «царем математиков»).

Рассказывают, что в возрасте трех лет он заметил ошибку, сделанную его отцом в расчетах. А семи лет мальчик пошел в школу. В то время в одной классной комнате занимались уче­ники разных классов. Чтобы занять первоклассников, пока он будет заниматься с третьим классом, учитель велел им сло­жить все числа от 1 до 100. Но не успел он закончить чтение условия задачи, как маленький Карл написал на своей гри­фельной доске ответ и положил на учительский стол.

С сожалением смотрел преподаватель на мальчика: ясно было, что за такой короткий срок он не мог сделать 99 сложе­ний. Остальные ученики терпеливо складывали числа, сби­ваясь, стирая написанное и снова складывали. Когда учитель закончил занятия с третьеклассниками, он взял со своего стола грифельные доски. Ни у кого не было правильного резуль­тата. И только на доске Карла стоял ответ: 5050, причем ни­каких вычислений- не было.

«Как же ты это сосчитал?» — спросил учитель.

«Очень просто,— ответил мальчик.— Я сложил 1 и 100, получил 101. Потом сложил 2 и 99, тоже получилось 101; 3 и 98— снова 101, и так до 50+51=101. Значит, надо сло­жить 50 слагаемых по 101 каждое, то есть умножить 101 на 50. А это и равно 5050».

Изумленный учитель понял, что встретил самого способного ученика в своей жизни. В дальнейшем Гаусс сделал много замечательных открытий в математике.

Ученица объясняет условие: На экране записано 20 чисел: 1,4,7,10,13,16,19,22,25,28,31,34,37,40,43,46,49,52,55,58.

Я не буду на них смотреть. Назовите номер числа, и я мгновенно назову это число. (2-3 числа) Можете объяснить, как мне это удается? (выслушивает версии) Прогрессия здесь задана формулой a_n=3n-2. Мне остается подставить в формулу номер и посчитать.

Номера верных ответов запиши через точку с запятой

Вариант 1.

1. Из предложенных последовательностей выберите ту, которая может являться арифметической прогрессией:

1) 1; 11; 21; 31… 2) 1; 2; 4; 9; 16…

3) 2; 4; 8; 16… 4) 7; 8; 7; 8…

2. Перед вами четыре числа. Какое из этих чисел является шестым членом последовательности натуральных чисел, кратных 5:

1) 25; 2) 30; 3) 40; 4) 35?

3. Чему равна сумма пяти первых членов арифметической прогрессии, если а₁=3, а₅= 25

1) 65 , 2) 80 , 3) 70, 4) 75

4. Последовательность 4; -6… является арифметической прогрессией. Какое из предложенных чисел будет равно сумме восьми первых ее членов?

1) 312; 2) -24; 3) 77; 4) -248.

Номера верных ответов запиши через точку с запятой

Вариант 2.

1. Из предложенных последовательностей выберите ту, которая может являться арифметической прогрессией:

1) 2; 7; 12; 17… 2) 1; 2; 4; 9; 16…

3) 2; 4; 8; 16… 4) 7; 8; 7; 8…

2. Перед вами четыре числа. Какое из этих чисел является шестым членом последовательности натуральных чисел, кратных 3:

1) 24; 2) 18; 3) 21; 4) 12?

3. Чему равна сумма пяти первых членов арифметической прогрессии, если а₁=2, а₅= 28

1) 65 , 2) 80 , 3) 75, 4) 70

4. Последовательность 2; -4… является арифметической прогрессией. Какое из предложенных чисел будет равно сумме восьми первых ее членов?

1) 312; 2) -42; 3) -312; 4) -152.

Номера верных ответов запиши через точку с запятой

Вариант 1.

1. Из предложенных последовательностей выберите ту, которая может являться арифметической прогрессией:

1) 1; 11; 21; 31… 2) 1; 2; 4; 9; 16…

3) 2; 4; 8; 16… 4) 7; 8; 7; 8…

2. Перед вами четыре числа. Какое из этих чисел является шестым членом последовательности натуральных чисел, кратных 5:

1) 25; 2) 30; 3) 40; 4) 35?

3. Чему равна сумма пяти первых членов арифметической прогрессии, если а₁=3, а₅= 25

1) 65 , 2) 80 , 3) 70, 4) 75

4. Последовательность 4; -6… является арифметической прогрессией. Какое из предложенных чисел будет равно сумме восьми первых ее членов?

1) 312; 2) -24; 3) 77; 4) -248.

Номера верных ответов запиши через точку с запятой

Вариант 2.

1. Из предложенных последовательностей выберите ту, которая может являться арифметической прогрессией:

1) 2; 7; 12; 17… 2) 1; 2; 4; 9; 16…

3) 2; 4; 8; 16… 4) 7; 8; 7; 8…

2. Перед вами четыре числа. Какое из этих чисел является шестым членом последовательности натуральных чисел, кратных 3:

1) 24; 2) 18; 3) 21; 4) 12?

3. Чему равна сумма пяти первых членов арифметической прогрессии, если а₁=2, а₅= 28

1) 65 , 2) 80 , 3) 75, 4) 70

4. Последовательность 2; -4… является арифметической прогрессией. Какое из предложенных чисел будет равно сумме восьми первых ее членов?

1) 312; 2) -42; 3) -312; 4) -152.

В древнеегипетском папирусе Ахмеса (ок. 2000 лет. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.» В этой задаче речь идет об арифметической прогрессии.

В древнеегипетском папирусе Ахмеса (ок. 2000 лет. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.» В этой задаче речь идет об арифметической прогрессии.

В древнеегипетском папирусе Ахмеса (ок. 2000 лет. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.» В этой задаче речь идет об арифметической прогрессии.

В древнеегипетском папирусе Ахмеса (ок. 2000 лет. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.» В этой задаче речь идет об арифметической прогрессии.

В древнеегипетском папирусе Ахмеса (ок. 2000 лет. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.» В этой задаче речь идет об арифметической прогрессии.

В древнеегипетском папирусе Ахмеса (ок. 2000 лет. до н. э.) приводится такая задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.» В этой задаче речь идет об арифметической прогрессии.

10

«progression»

движение вперед

успех

Чтобы идти вперед, чаще оглядывайтесь назад, ибо вы забудете, откуда вы вышли, и куда вам нужно идти.

Л. Андреев

Устная работа

Являются ли арифметическими прогрессиями последовательности чисел:

• 3; 7; 12; …
• 28;31;34…

Найдите разность арифметической прогрессий: 28; 31;34;…

Соотнесите график и формулу арифметической прогрессии, которая его задает

• Какие из формул задают арифметическую прогрессию:

a n =3n+1

a n =3n 2 +1

a n =-3n+1

a n =

• Продолжите арифметическую прогрессию: 28; 31;34;…
• Найдите одиннадцатый член этой прогрессии

100

1;2;3;4;…

1+100=101

2+99=101

3+98=101

…………

50+51=101, т.е.

101 •50=5050

Формулы n первых членов арифметической прогрессии

S n – сумма n первых членов арифметической прогрессии

Задача: Найдите сумму n первых членов арифметической прогрессии, если известны ее первый и n-ый члены.

Найдем суммы:

a 1 + a n ,

a 2 + a n-1 = (a 1 + d)+(a n - d )= a 1 + a n , очевидно, что

a 3 + a n-2 =a 1 + a n и т.д.

Таких пар будет n /2.

Значит, S n = (a 1 + a n )• n /2, т. е.

Дано:

(a n )- арифметическая прогрессия

a 1 , a n

S n -?

• Используя формулу

решите № 603а стр.151. .

• Решите №605(а) стр.151

Сверим решение:

Сверим решение:

МИНУТКА ОТДЫХА

1; 4 ; 7 ; 10 ; 13 ; 16 ; 19 ; 22 ; 25 ; 28 ; 31 ;

34 ; 37 ; 40 ; 43 ; 46 ; 49 ; 52 ; 55 ; 58.

Задача от строителя

• Вертикальные стержни конструкции имеют следующую длину: наименьший 5 дм, а каждый следующий на 2 дм длиннее. Найдите длину семи таких стержней.

Ответ: 77 дм –длина семи таких стержней

Задача от физика

• Решите № 614 стр. 152

Ответ: 125 м – глубина шахты

Задача от лесозаготовителя

• При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основание положить 12 бревен?

Решение задачи от лесозаготовителя

Дано: арифметическая прогрессия: а 1 =12 ,а 2 =11,а n =1

Найти: S n

Решение: a n = a 1 + d(n – 1)

d=11-12=-1

1=12-1(n-1)

n=12

Ответ: 78 бревен в одной кладке

Домашнее задание

папирус Ахмеса (ок. 2000 лет. до н. э.)

«Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялось 1/8 меры.»

п.26 выучить формулы

№ 604, №607,

на повторение № 619

Математика –

царица наук,

а арифметика – царица

математики.

К.Гаусс