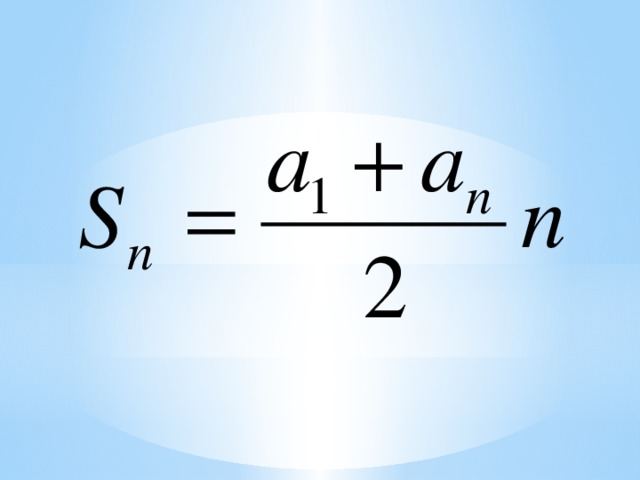3
Самоанализ урока
«Формула суммы n первых членов арифметической прогрессии». 9 класс.
Дифференцированный процесс обучения – это широкое использование различных форм, методов обучения и организации учебной деятельности на основе результатов психолого-педагогической диагностики учебных возможностей, склонностей, способностей учащихся. Использование этих форм и методов, одним из которых является уровневая дифференциация: основываясь на индивидуальных особенностях обучаемых, создаются благоприятные условия для развития личности.
Обращение к данной теме обусловлено желанием повысить познавательную активность учащихся, их интерес к урокам математики, развивать коммуникативные способности.
Кроме этого, не все школьники способны в одинаковой степени познать науку, поэтому в школьной практике применяется дифференцированный подход к учащимся.Дифференцированный подход целесообразно осуществлять на определенных этапах урока.
Дифференцированное введение нового материала осуществляю сочетанием двух подходов – дифференцированного и проблемного.
Проблемную ситуацию создаю путем применения следующих методических приемов:
Подвожу учащихся к противоречию и предлагаю самим найти способ его разрешения;
При ответе на один и тот же вопрос рассматриваем разные точки зрения, обсуждая и доказывая их;
Побуждаю учащихся делать сравнения, обобщения, выводы из ситуации, сопоставлять факты;
Вместе с учащимися ставим конкретные вопросы (на обобщение, обоснования, конкретизацию, логику рассуждения);
Ставлю перед учащимися проблемные задачи.
Использую следующие методы и средства при дифференциации по уровням усвоения материала:
игровой метод;
создание проблемно-поисковых ситуаций;
моделирование;
алгоритмический метод;
групповую работу;
систему подсказок учителя, направленных на активизацию мыслительной деятельности учащихся;
исследовательские методы;
компьютер (презентация).
Разноуровневые задания облегчают организацию занятий в классе, создают условия для продвижения школьников в учебе в соответствии с их возможностями, создают в классе благоприятный психологический климат. У ребят возникает чувство удовлетворения после каждого верно решенного задания. Успех, испытанный в результате преодоления трудностей, дает мощный импульс повышению познавательной активности. У учащихся, в том числе и слабых, появляется уверенность в своих силах, они уже не чувствуют страха перед новыми задачами, рискуют пробовать свои силы в незнакомой ситуации, берутся за решение задач более высокого уровня. Все это способствует активизации мыслительной деятельности учащихся, созданию положительной мотивации к учению. При таком способе подачи материала, его отработке у учащихся развивается логическое мышление, развиваются коммуникативные способности, повышается активность. Выполнение любых заданий необходимо контролировать. При любом виде контроля ученик должен знать критерии оценок. На своих уроках часто использую такие виды контроля, как самоконтроль и взаимоконтроль. Чтобы закрепить ситуацию успеха, созданную на уроке, учащиеся в домашних условиях выполняют дифференцированную домашнюю работу. Каждый ребёнок – это индивидуальность и работать с ним надо осторожно и с любовью. В своей педагогической деятельности я придерживаюсь следующих принципов работы с учащимися:
от творчества учителя к творчеству ученика;
предупредить, а не наказать незнание;
мотивация, а не констатация;
ученик должен испытать успех;
обучать школьников на эмоциях радости;
развивать мотивацию к самостоятельному поиску решений;
сделать главной заповедью своей педагогической деятельности: “Не навреди”.
В итоге такой деятельности ученики научены самостоятельно добывать знания, у них развито логическое мышление, они умеют составлять устный и письменный ответ на поставленный вопрос, анализировать ситуацию, высказывать свое мнение, моделировать и составлять алгоритмы решения задач, приводить и обосновывать собственные примеры, применять полученные знания при решении задач, требующих творческого подхода
Общие сведения:
Урок алгебры проведен в 9 классе на тему: «Формула суммы n первых членов арифметической прогрессии». Одна из опорных тем 9 класса. По программе запланировано 7 часов, а данный урок был четвертым по плану.Класс организован, дисциплинирован.
На уроке присутствовало 18 человек. Из них 60 % с достаточным уровнем, 2% - с высоким.
На уроке решались следующие задачи:
Образовательные: формировать у учащихся умение решать типовые математические задачи на вычисление суммы членов арифметической прогрессии; применять теорию в конкретных ситуациях.
Развивающие: обучение учащихся самостоятельному приобретению знаний путем творческого поиска и решения проблемных вопросов и ситуаций.
Воспитательные: формирование личностных качеств: точность и ясность словесного выражения мысли; сосредоточенность и внимание; настойчивость и ответственность. Профориентация.
Задача:обеспечить прочное и сознательное овладение учащимися навыками вычисления суммы первых членов арифметической прогрессии
Содержание урока соответствует учебной программе, поставленным задачам, способствовало формированию умения решать типовые математические задачи на вычисление суммы членов арифметической прогрессии; применять теорию в конкретных ситуациях.Содержание урока способствовало развитию аналитического мышления.
По типу урок – усвоение новых знаний, поэтому при построении урока придерживалась следующей логической схемы:
- мотивация – актуализация – первичное восприятие материала – применение знаний в сходной ситуации – самоконтроль – контроль.
Знания подлежат прочному усвоению, их объем заложен в программе и они должны быть усвоены каждым учеником. Материал, близко примыкающий к основному, который расширяет и углубляет его и одновременно закладывает основу для дальнейшего изучения.В соответствии с поставленными целями и содержанием материала урок строился по следующим этапам:
1.Организационный этап урока, включающий в себя проверку подготовленности учащихся к работе, направлен на психологический настрой и организацию вниманию школьников. С использованием словесных методов сообщилась тема и цели урока.Учащиеся внимательно прослушали постановку целей урока, получили положительный настрой.
2.На втором этапе проводилась проверка знаний учебного материала, изученного ранее: в ходе фронтального опроса теоретического материала с ребятами повторили определение арифметической прогрессии, понятие разности прогрессии. У ребят появилась возможность еще раз услышать и проговорить определение арифметической прогрессии. Работа с № 354, выполненным учащимися к данному уроку с целью проверки знаний формулы n- ого члена прогрессии и дальнейшего её применения.Индивидуальные задания по карточкам. Продуманные дифференцированные задания позволили учесть индивидуальные особенности учащихся. Решая посильные задания, ребята чувствовали себя комфортно, многие старались выполнить задание сложнее своих реальных возможностей.
3. На следующем этапе урока, подготавливая учащихся к усвоению нового материала, использовали результаты домашней задачи № 354, задачу профессора С.А. Рачинского. (сообщение ученика), а также задачу – стихотворение, историческую справку о немецком математике Гауссе. Это вызвало возбуждение у учащихся интереса к задаче, развитие у них внимания, умение использовать аналогию, обобщение, умение применять знания.
Поиск путей решения проходил в результате самостоятельного исследования, проведенного под руководством учителя. Таким образом, постановка учебной задачи обеспечила мотивацию понятия. Одновременно шла эффективная работа над развитием речи, мыслительных операций, о чем свидетельствовала деятельность учащихся.
4.Открытие детьми нового знания: вывод формулы суммы n первых членов арифметической прогрессии проходил под руководством учителя. Учащиеся очень быстро справились с этим видом работы. С помощью частично – поискового метода не только вывели формулу, но и поставили перед собой задачи.
5.В процессе первичного закрепления примеры решались с комментированием. При комментировании шла работа над речевой деятельностью, в которой они своими словами выражали суть выполняемых преобразований.
Постановка проблемы была поставлена в ходе решения задачи, которая вызвала у детей интерес, удивление, напомнило им уже известное. Само задание не вызвало затруднения в нахождении результата, таким образом проблема мотивировала поиск вычислительного навыка.
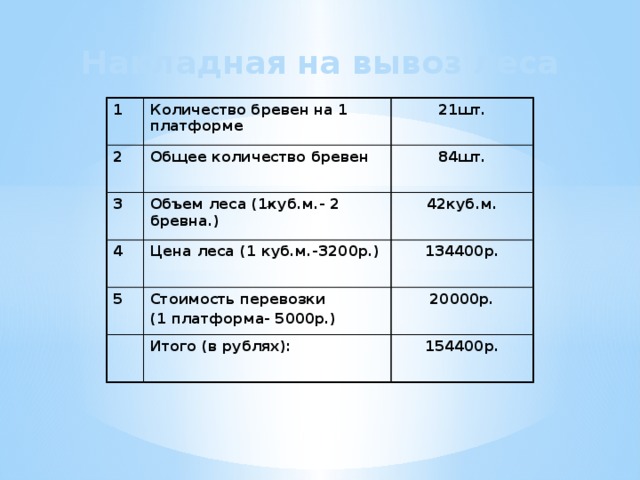
Учитывая, многие учащиеся планируют связать свою жизнь с лесным хозяйством, задания выбраны с учетом их профессиональной ориентации. Необходимо представить себя работником лесной промышленности. Этап обучающей самостоятельной работы показал, что каждый ребенок смог себя проверить, осознать: все ли он понял, запомнил ли обе формулы. Считаю, что на данном этапе каждый ученик смог пережить ситуацию успеха, убедиться, что изученный материал им освоен, о чем свидетельствовали результаты их самооценки.
Дифференцированный подход к учащимся на уроке был использован при проверке домашнего задания, при проведении самостоятельной работы, а также при выборе домашнего задания.
Контроль усвоения материала осуществлялся в форме самоконтроля, взаимоконтроле, обратной связи, проверки тетрадей.
Реализация принципов обучения:
- принцип научности содержания учебного материала – содержание обучения знакомило с понятиями арифметической прогрессии и формулами суммы n первых членов прогрессии.
- принцип систематичности и последовательности в овладении нового материала – опора на прочно освоенные знания по курсу «Алгебра» за курс основной школы;
- принцип доступности обучения заключался в том, что для учащихся для начала предлагались несложные задания;
- принцип учета индивидуальных особенностей учащихся заключался в том, что учащиеся выполняют задания, соответствующие уровню их учебных возможностей, исами оценивают свои способности;
- принцип прочности – связь нового материала с ранее усвоенным обеспечивает прочность знаний;
- принцип наглядности.
Методы обучения:
Соответствовали задачам урока и по источнику передачи знаний были:
- словесные (рассказ, эвристическая беседа);
- наглядные (демонстрация);
- практические
по уровню самостоятельности учащихся:
проблемно – поисковые, репродуктивные,
по аспекту мышления:
продуктивные (самостоятельное решение),
Общие результаты урока:
План урока выполнен, цели реализованы: учащиеся научились решать типовые математические задачи на вычисление суммы членов арифметической прогрессии; применять теорию в конкретных ситуациях.
Домашнее задание соответствует нормативным требованиям, дифференцировано, дано с комментарием.