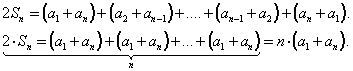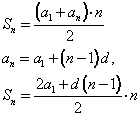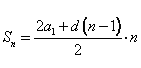Конспект урока по алгебре для 9 класса «Сумма n-первых членов арифметической прогрессии»

Целью данной работы является представление урока по теме «Сумма n-первых членов арифметической прогрессии». Данный урок был проведен в 9а математическом классе, изучение алгебры в котором осуществляется по УМК для углубленного изучения алгебры в 8-9 классах. На изучение алгебры по учебному плану отведено 6 часов.

В данном УМК:

• Учебники для 8 и 9 классов, авторы: Н.Я. Виленкин и др.,

• Дидактические материалы по алгебре для 8-9 классов, авторы: Г.С. Сурвилло и др.,

• Сборник задач по алгебре для 8-9 классов, авторы: М.Л. Галицкий и др.

По рабочей программе на тему «Последовательности» отводится 20 часов. Представленный урок – шестой в данной теме.

Тип урока: Урок изучения нового материала.

Оборудование: мультимедийное оборудование, раздаточный материал, презентационные слайды.

Цели урока: ввести формулу суммы членов конечной арифметической прогрессии, формировать умение применения алгоритма для нахождения суммы членов конечной арифметической прогрессии.

Задачи урока:

Обучающие - уметь применять полученные знаний на практике, знакомство с историческими аспектами данной темы.

Развивающие – развитие математической интуиции, логики, кругозора, реализация принципов связи теории и практики, формирование умения проводить доказательства, развитие познавательного и прикладного интереса, развитие логического мышления и вычислительной культуры.

Воспитательные - воспитание ответственного отношения к умственному труду, развитие навыков сотрудничества, развитие внимания к действиям учителя, воспитание дисциплинированности, собранности.

Этапы урока:

1. Организационный этап (1 мин).

2. Этап подготовки к активному сознательному усвоению знаний (10 мин).

3. Этап изучения нового материала (8 мин).

4. Этап закрепления изученного материала (12 мин).

5. Этап проведения контроля (7 мин).

6. Этап инструктажа по домашнему заданию (1 мин).

7. Этап подведения итогов урока (1 мин).

Ход урока

1. Организационный этап.

Здравствуйте, ребята, садитесь. Откройте тетради, запишите, число…., классная работа.

II. Этап подготовки к активному сознательному усвоению знаний

Задание классу:

1. На слайде представлены некие числовые последовательности.

а) продолжить ряд (записать в тетрадь)

Устно:

Продолжите ряд:

1. 1;2;4;8;16…..

2. 4;7;10;13……..

3. 1;2;3;6;12…..

4. 1;6;11;16;21….

5. 1;4;9;16;25…..

6. 16;12;8………

В парах обсудите варианты продолжения последовательностей. При проверке заслушаем 6 пар.

Проверка. (1- каждое последующее число в два раза больше предыдущего, 2- каждое последующее число на 3 больше предыдущего, 3- каждое последующее число на 1,2,3,4…. больше предыдущего, 4- каждое последующее число на 5 больше предыдущего, 5 – последовательность квадратов натуральных чисел, 6- каждое последующее число на 4 меньше предыдущего).

У кого было все правильно, ставит себе «+».

б) Выписать в тетрадь номера последовательностей, являющихся арифметическими прогрессиями.

Проверить в парах.

Одна пара представляет свой вариант. (Согласны, не согласны, почему…)

У кого было все правильно, ставит себе «+».

2.Почему последовательности 2); 4); 6) являются арифметическими прогрессиями?

(Каждый член этих последовательности больше предыдущего на одно и то же число. Следовательно, разность между предыдущим и последующим членами остается постоянной, а это означает, что последовательность - арифметическая прогрессия.)

Во время работы класса три ученика оформляют на доске решение домашней работы.

Задача 1.

Дана арифметическая прогрессия: a₄ =18, a₈=38. Найти и d.

Решение:

1. d= (38 -18)/(8-4)

d= 5

2. a₄₌ а1+5+5+5= a₁ + 15

а₁ = 18 – 15 = 3

Ответ: а₁ = 3 и d = 5.

Задача 2.

Сколько положительных членов в прогрессии 15,6; 13,5; 11,4……

Решение:

a_n= a₁+ d (n – 1), где a₁=15,6; d= -2,1

a_n = 15 ,6 -2,1 (n – 1)

по условию 15,6 -2,1 (n – 1) 0

15,6-2,1 n + 2,1 0

17,7 2,1 n

n

n

т.к для натуральных значений n выполняется условие то n=8

Ответ: 8

Задача 3.

При каком значении х три подряд идущих числа 4х; х-1; 12 составляют арифметическую прогрессию? Найти эти числа.

Решение: по свойству арифметической прогрессии 2*( х-1 ) = 4х + 12

2х-2=4х+12

-2х = 14

Х=-7

Ответ: -28; -8; 12.

Ученики представляют свои решения классу.

Дополнительные вопросы выступающим ученикам:

1.Дайте определение арифметической прогрессии.

(Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом. или Последовательность у которой an+1= an + d , где а и d любые заданные числа, называется арифметической прогрессией.

2. Дать характеристику числу d. (Число d- называется разностью арифметической прогрессии, причем если d 0 то прогрессия является монотонно возрастающей, если d d=0 невозрастающей.)

2. Как найти n-ый член арифметической прогрессии?

(Используя формулу n-ого члена прогрессии a_n=а₁+(n-1)d)

Во время проверки домашней работы 1 ученик заполняет таблицу у доски.

Ученикам предлагается себя оценить.

За каждую верно выполненную задачу ставим себе «+».

III. Этап изучения нового материала.

1. На слайде задача в стихах:

Задача очень непроста:
Как сделать, чтобы быстро
От единицы и до ста 
Сложить в уме все числа?
Пять первых связок изучи, 
Найдёшь к решению ключи.

а) Найти сумму чисел от 1 до 10. (Ученики решали эту задачу и знают способ решения: 11*5=55)

Проверка в парах. Одну пару заслушиваем.

б) Найти сумму всех натуральных чисел от 1 до 100, т.е. вычислим сумму

S = 1+2+3+4+5+........+99+100.

Проверка в парах. Одну пару заслушиваем.

S = 101*50 = 5050

Слайд. Гаусс К.Ф.

Много замечательных историй мы знаем о великих математиках. Одной из них является легенда о Карле Гауссе.

Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс вероятно рассуждал так: «Сумма первого и последнего слагаемого равна 101, сумма второго и предпоследнего слагаемого, тоже 101 и ничего странного в этом нет. Второе слагаемое на единицу больше первого, а предпоследнее на единицу меньше последнего, так что сумма должна быть такой же. То же будет происходить и с каждой новой парой чисел. Таких сумм 50, так как всего чисел 100 и все они разделены на пары. Значит, вся сумма равна числу 101 умноженному на 50. И Гаусс подсчитал, что сумма равна 5050» и мгновенно получил результат.

Эту задачу вы решили, используя свойство присущее всем арифметическим прогрессиям.

Ее решение предложено в учебнике на странице 248.

Учащиеся разбирают решение задачи, 1 ученик отвечает у доски:

Запишем сумму данных чисел, а под ней – те же слагаемые в обратном порядке:

S = 1+2+3+4+5+........+99+100

S = 100+99+…….+5+4+3+2+1

Сложим почленно эти два равенства. Каждая пара слагаемых даст один и тот же результат 101.

2 S = 101+101+101+101+……….+101 из числа 100 слагаемых

2 S = 10100

S = 5050

Этот же прием можно использовать и для вычисления суммы n-первых членов арифметической прогрессии. В тетради записываем тему: Сумма n-первых членов арифметической прогрессии.

Доказательство теоремы ученикам предложено провести самостоятельно. Те, кто затрудняется, могут воспользоваться учебником. В учебнике на стр. 249 оно представлено.

Доказательство теоремы 1 ученик проводит у доски, ученики записывают доказательство в тетрадь.

Теорема: Сумма первых n членов арифметической прогрессии

равна полусумме первого и n-го ее членов, умноженной на число членов n, т.е.

Пусть сумма первых n членов арифметической прогрессии равна тогда:

Складывая эти равенства почленно, получим:

Отсюда имеем формулу:

Учитывая, что a_n=а₁+(n-1)d;

получим

IV. Этап закрепления изученного материала.

На слайде предложены пять задач из УМК «Математика. Подготовка к ГИА». Их необходимо решить самостоятельно. У кого есть вопросы, можно их задавать учителю по ходу решения индивидуально.

5 желающих учеников решают задачи на доске (за шторками)

1)Найти сумму 35 первых членов арифметической прогрессии 2;4;6;8;……..

2) Найти сумму ста первых четных натуральных чисел.

3) Найти сумму 40 первых членов арифметической прогрессии, если a₂ = 7, а₄ =11.

4) Найдите сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно, если первый член равен 10 и разность равна 3.

5) Турист, поднимаясь в гору за первый час достиг высоты 580 м, а за каждый следующий час поднимался на высоту на 40 м меньше, чем в предыдущий. За сколько часов он достигнет высоты 2500 м, поднимаясь от подножия горы.

При проведении проверки шторки открываются, ученики представляют свои решения. Ученики задают им вопросы на понимание и по теории.

Выступающим ученикам предлагается оценить себя.

Задача 1.

Найти сумму 35 первых членов арифметической прогрессии 2;4;6;8;……..

Решение:

a₃₅ = а₁ + ( n - 1)d;

a₃₅ = 2 + (35-1) 2=70

S = (2 + 70) *35/2 =1260.

Ответ: 1260

Задача 2.

Найти сумму ста первых четных натуральных чисел.

Решение:

2;4;6;8;…….2n.- это арифметическая прогрессия с разностью 2.

S = (2 + 200) *100/2 =10100.

Ответ:10100

Задача 3.

Найти сумму 40 первых членов арифметической прогрессии, если a₂ = 7, а₄ =11

Решение: Зная второй и четвертый члены арифметической прогрессии, найдем a₁ и d

d = (11 – 7) / (4 – 2) = 2

a₁₌ a₂ – d =7 – 2 = 5

S = (2*5 +2(40 – 1))*40/2=(15+78)*20 = 93*20 = 1860

Ответ:1860

Задача 4.

Найдите сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно, если первый член равен 10 и разность равна 3.

Решение:

a_n = а₁ + ( n - 1)d

а₁₅ = 10 + 3( 15 - 1) = 10 + 42 = 52

a₃₀ = 10 + 3( 30 - 1) = 10 + 87 = 97

т.к с 15-го по 30-ый 16 членов прогрессии, то

S = (52 +97)*8 = 1192

Ответ: 1192.

Задача 5.

Турист, поднимаясь в гору за первый час достиг высоты 580 м, а за каждый следующий час поднимался на высоту на 40 м меньше, чем в предыдущий. За сколько часов он достигнет высоты 2500 м, поднимаясь от подножия горы.

Решение:

a_{1= 580}

d =-40

S= 2500

Найдем n. Воспользуемся формулой:

Решим уравнение:

(1160-40(n-1))*n=5000

(1160-40n+40)n=5000

1200n-40n²-5000=0

n²-30n+125=0

n1=5, n2=25

Отбираем число 5 по смыслу задачи.

Ученикам предложено задать вопросы на понимание.

V. Этап проведения контроля

Решить самостоятельно предложенные на слайде задачи:

Вариант 1

1. а₁= - 3; d=7. Найдите S₇.

2. (а_n): 5; 2; -1; -4;… арифметическая прогрессия. Найдите S₂₀.

Вариант 2

1. а₁= - 2; d=9. Найдите S₇.

2. (а_n): 7; 5; 3; 1;…арифметическая прогрессия. Найдите S₂₀.

Учащиеся выполняют решение, затем самопроверку, сравнивая полученные ими ответы с представленными верными ответами на слайде.

За каждую верно выполненную задачу ставим себе «+».

Ответы к тесту

№ п/п	Вариант 1	Вариант 2
1.	S7=108	S7=175
2.	S20= - 470	S20=240

VI. Этап инструктажа по домашнему заданию.

П.2 стр. 248, ГИА № 7.14 (2),

№39; 42 или задание повышенной сложности №44; 45.

VII. Этап подведения итогов урока, рефлексии.

Ученикам предложено оценить свою работу на уроке.

7 плюсов – «5», 5,6 плюсов – «4», 3,4 плюса – «3», 1,2 плюса – «2», о плюсов – «1»

Поднимают руки, кто поставил себе «5», «4», «3».

Учитель выставляет оценок за урок учащимся с учетом самооценки.