Урок геометрии в 8 классе
«Площади треугольника и трапеции»
ЦЕЛИ УРОКА:
ПОЗНАВАТЕЛЬНЫЕ:
Совершенствование навыков и умений в решение задач по теме «Площадь»,
Формирование видения изученной закономерности в различных ситуациях
РАЗВИВАЮЩИЕ:
Развитие умений сопоставлять, систематизировать знания.
Развитие умения строить логическую цепочку, ведущую к умозаключению
ВОСПИТАТЕЛЬНАЯ:
Воспитание активности, наблюдательности, культуры умственного труда.
ОБОРУДОВАНИЕ УРОКА:
линейка, плакаты, раздаточный материал, карточки, доска – задачи на готовых чертежах.
СТРУКТУРА УРОКА:
Организационный момент
Сообщение темы, целей и задач урока
Актуализация знаний и умений
Систематизация знаний
а) теоретический опрос
б) решение задач по готовым чертежам
Применение учащимися знаний в стандартных условиях
Первичное применение приобретенных знаний в самостоятельной работе
Итоги урока и сообщение домашнего задания.
Ход урока:
Организационный момент
Сообщить тему урока, сформулировать цели урока.
Учитель: Здравствуйте! Сегодня на уроке мы закрепим знания по теме «Площади треугольника и трапеции».
II. Актуализация знаний учащихся
1. Теоретический опрос.
Учитель: Сформулируйте теоремы о площадях треугольника и трапеции.
Ученик 1: Площадь треугольника равна половине произведения его основания на высоту:
S=1/2a·h
Ученик 2: Площадь трапеции равна полусумме ее оснований на высоту:
S=1/2(a+в)h
Учитель: Существуют ли еще какие-нибудь формулы для вычисления площади треугольника?
Ученик 3: Формула Герона:
SΔ=√р(р-а)(р-в)(р-с),
где р=(а+в+с)/2, а, в и с — стороны треугольника
Ученик 4: Формула для вычисления площади прямоугольного треугольника:
S=1/2а▪в,
где а и в катеты треугольника.
2. Решение задач по готовым чертежам (фронтальная работа с классом).
Учитель: Теперь рассмотрим несколько задач (доска оформлена заранее).
Н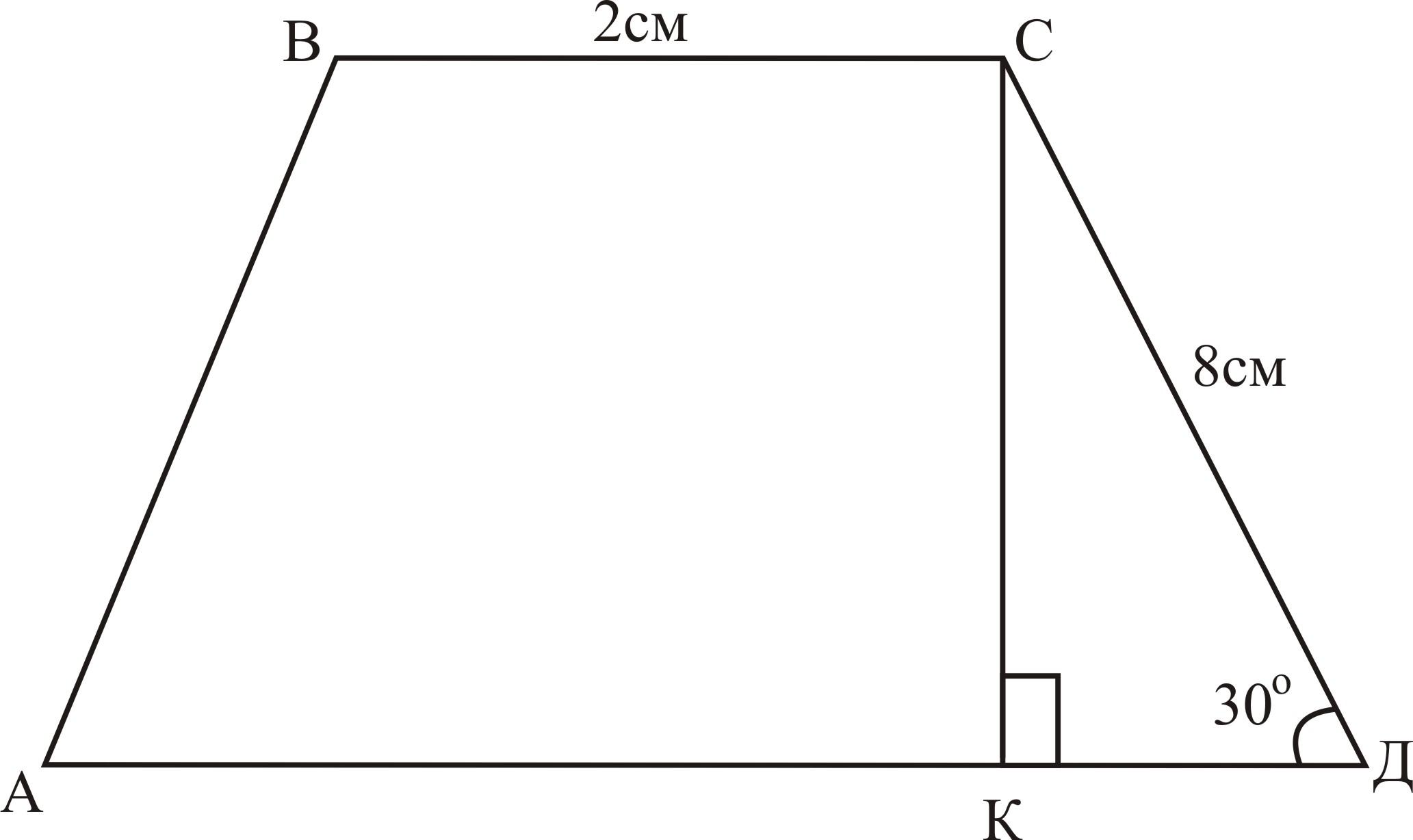 айдите площади фигур.
айдите площади фигур.
Деятельность ученика
а) АВСД — трапеция, АД=16см
Рассмотрим ΔСКД — прямоугольный, Д=30о, СК=1/2, СД=4см (по свойству прямоугольного треугольника)
SАВСД=1/2(2+16)▪4=36см2
Ответ: 36см2
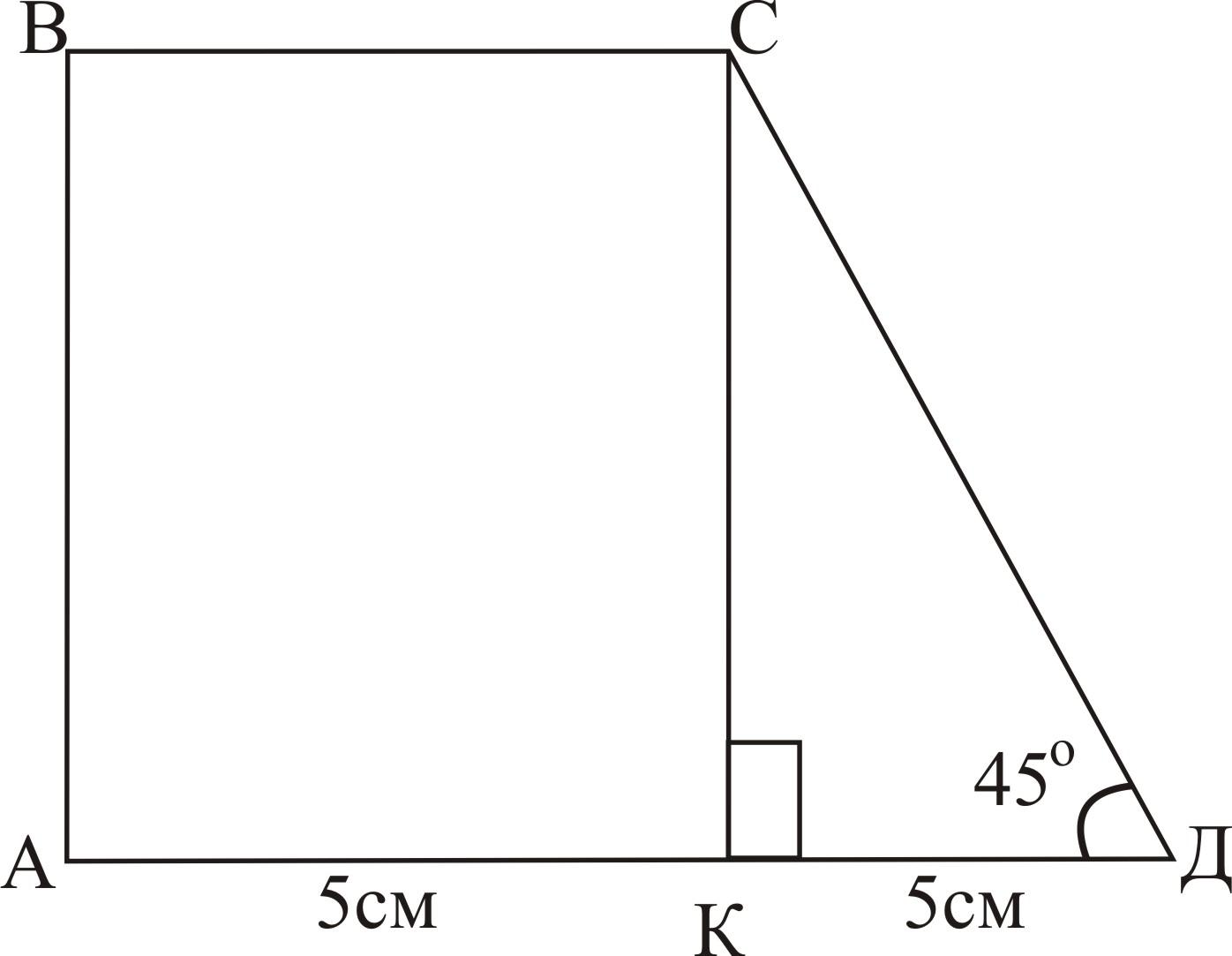
б) АВСД - трапеция
Рассмотрим ΔСКД — прямоугольный, равнобедренный, т.к. КСД=90о-45о=45о свойство прямоугольного треугольника)
Значит, СК=5см, ВС=5см (АВСК - прямоугольник)
SАВСД=1/2(10+5)▪5=37,5см2
Ответ: 37,5см2
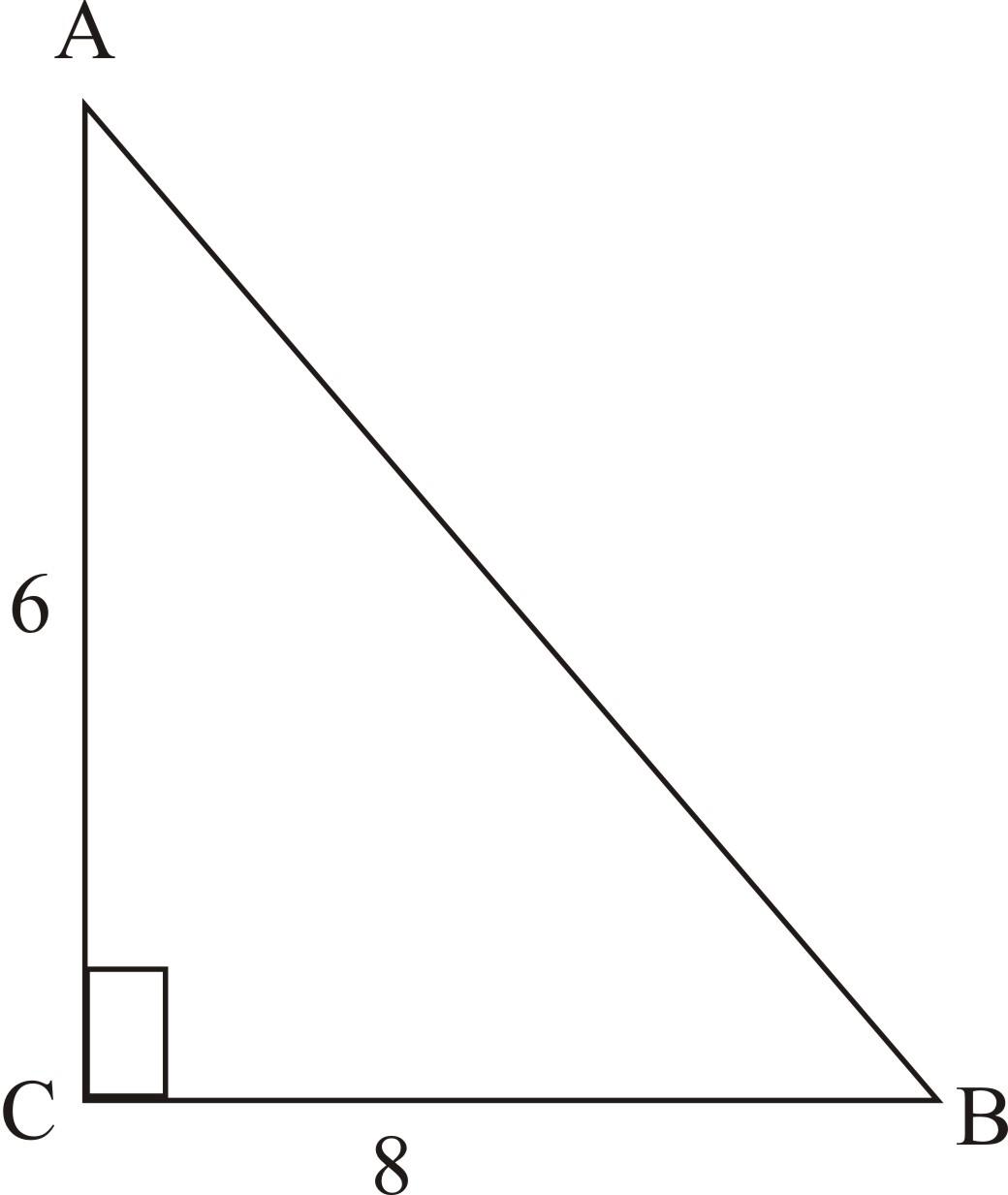
в)
ΔАВС — прямоугольный
SАВС=1/2▪6▪5=24см2
Ответ: 24см2
г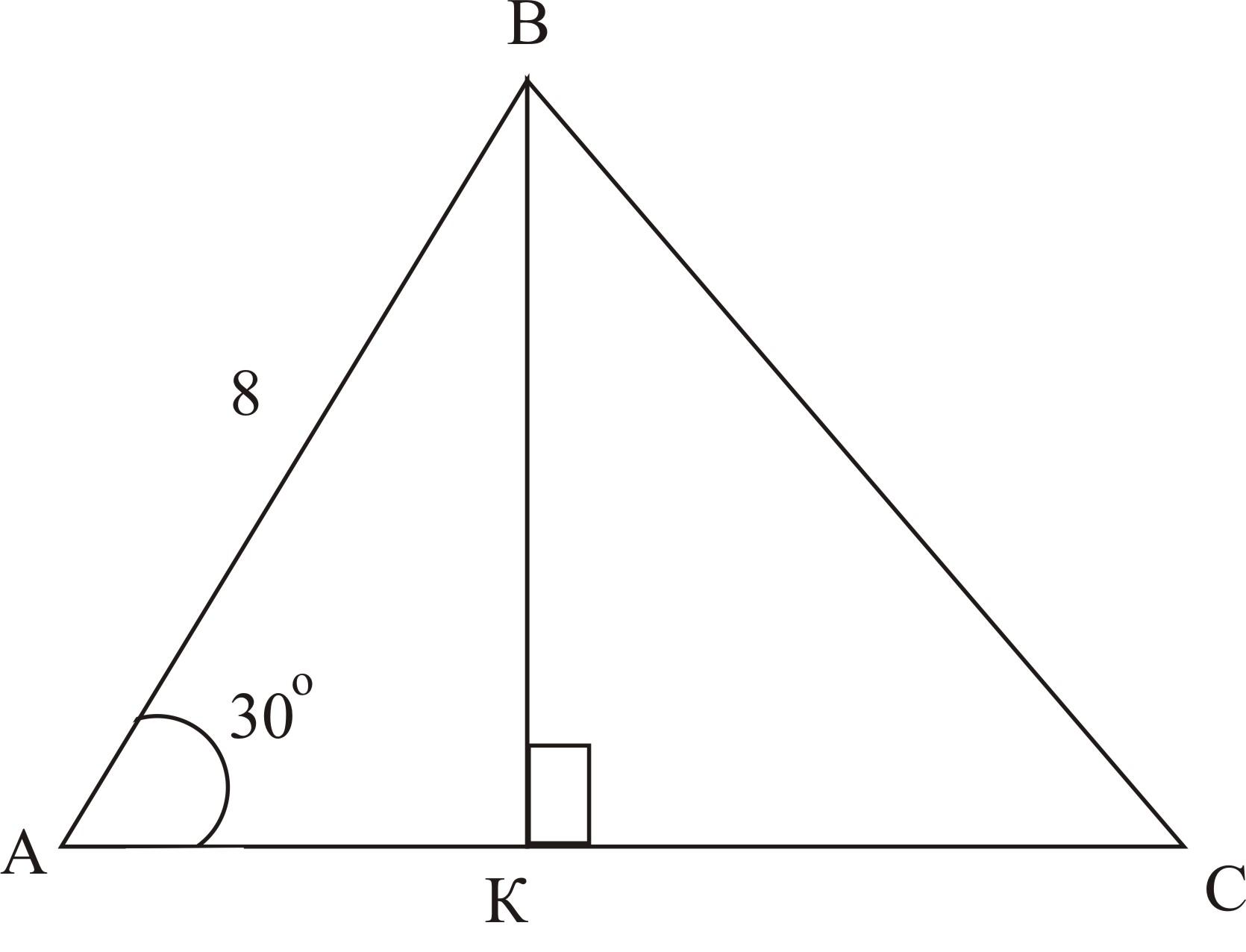 ) АС=15см
) АС=15см
Рассмотрим ΔСКД — прямоугольный,
А=30о; ВК=1/2; АВ=4см (по свойству прямоугольного треугольника)
SАВС=1/2▪15▪4=30см2
Ответ: 30см2
д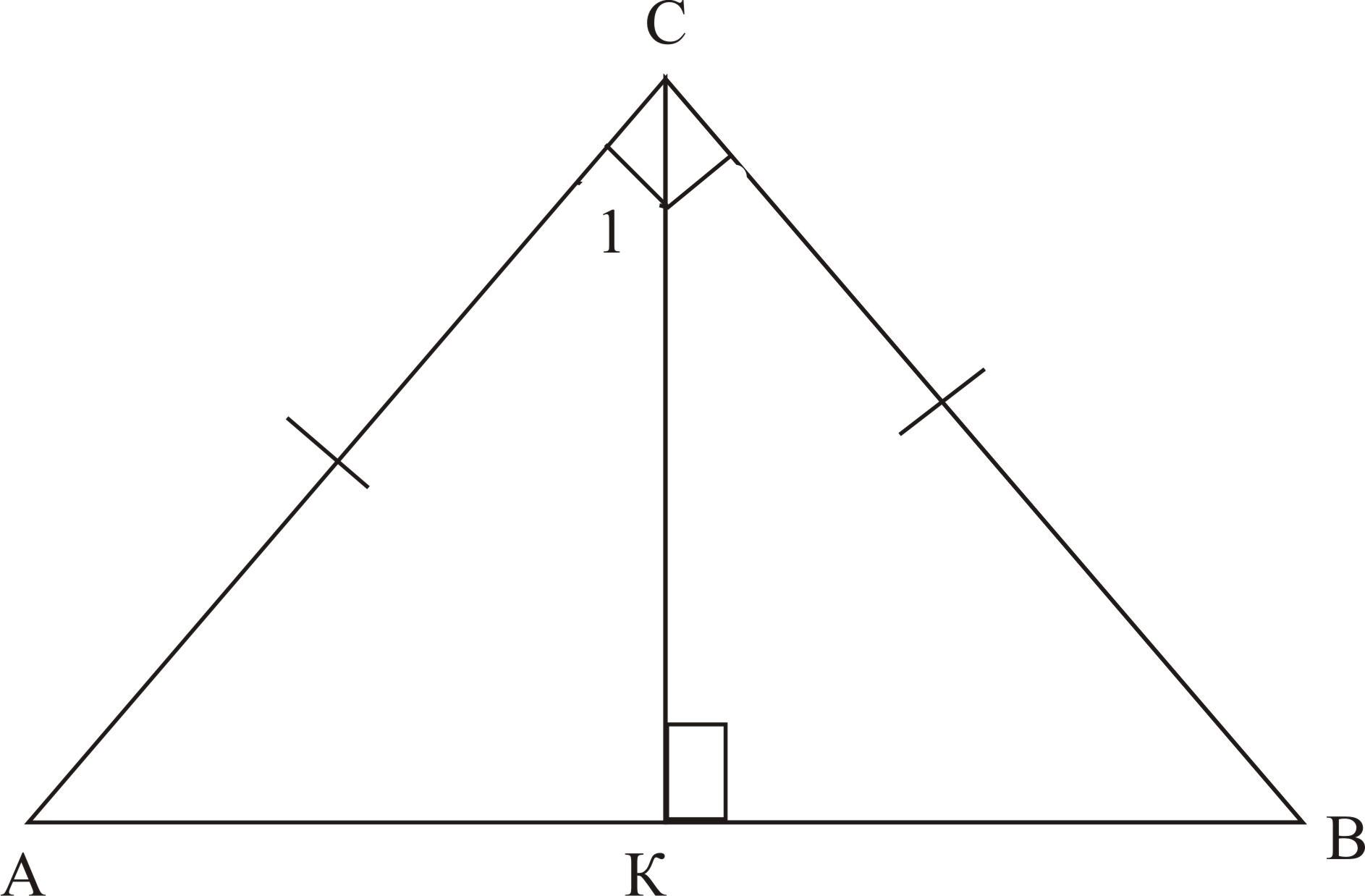 ) АВ=10см
) АВ=10см
ΔСКД — прямоугольный и равнобедренный, т.к. 1=45о (СК — биссектриса, по свойству равнобедренного треугольника)
А=90о-45о=45о (по свойству прямоугольного треугольника)
Значит, АК=КВ=СК=5см
SАВС=1/2▪10▪5=25см2
Ответ: 25см2
III. Закрепление изученного материала
Учитель: Запишем в тетрадях число и решим задачу №480(б) (один ученик работает у доски, остальные в тетрадях)
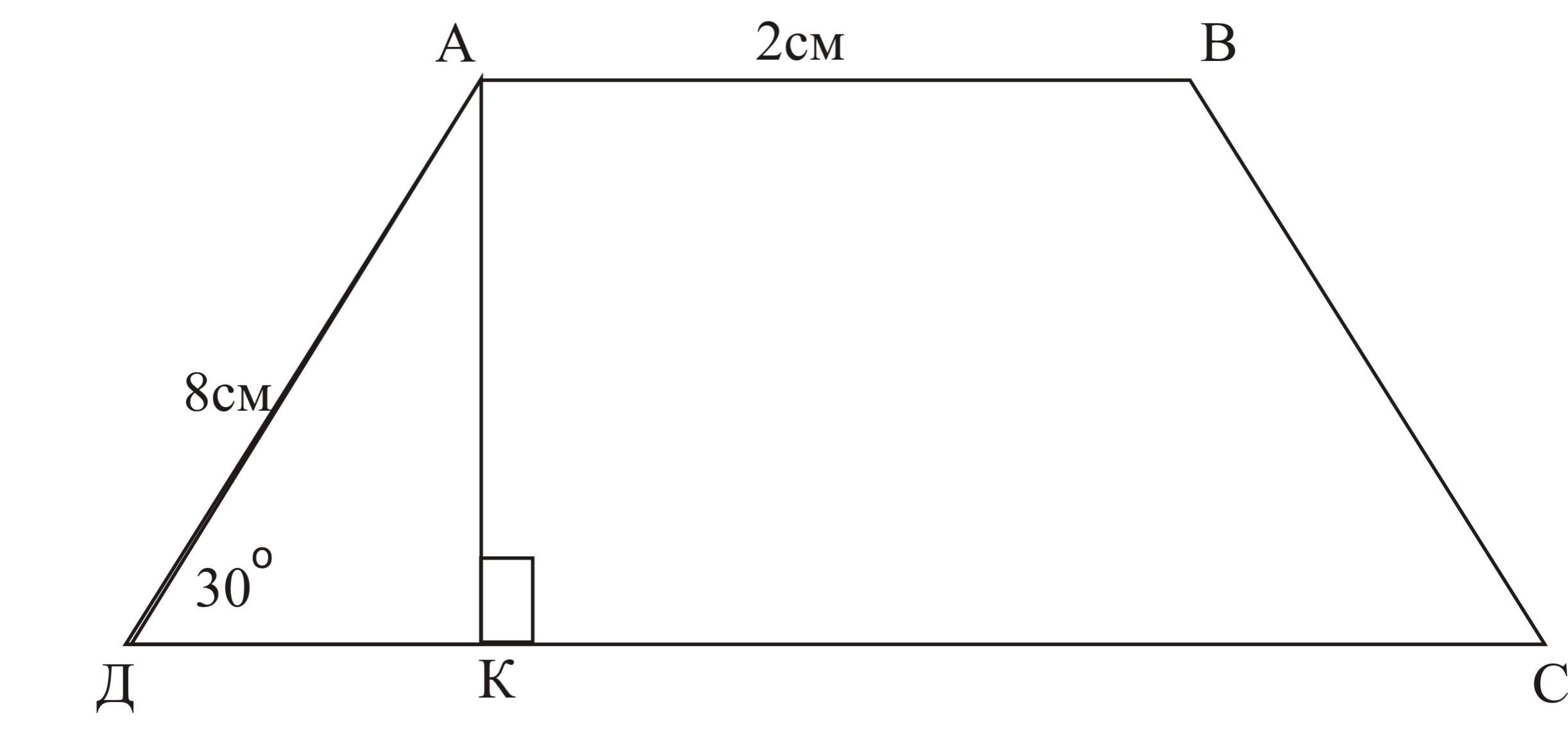 Дано:
Дано:
АВСД — трапеция
АВ=2см, ДС=10см, АД=8см, Д=30о
Найти: SАВСД
Решение:
1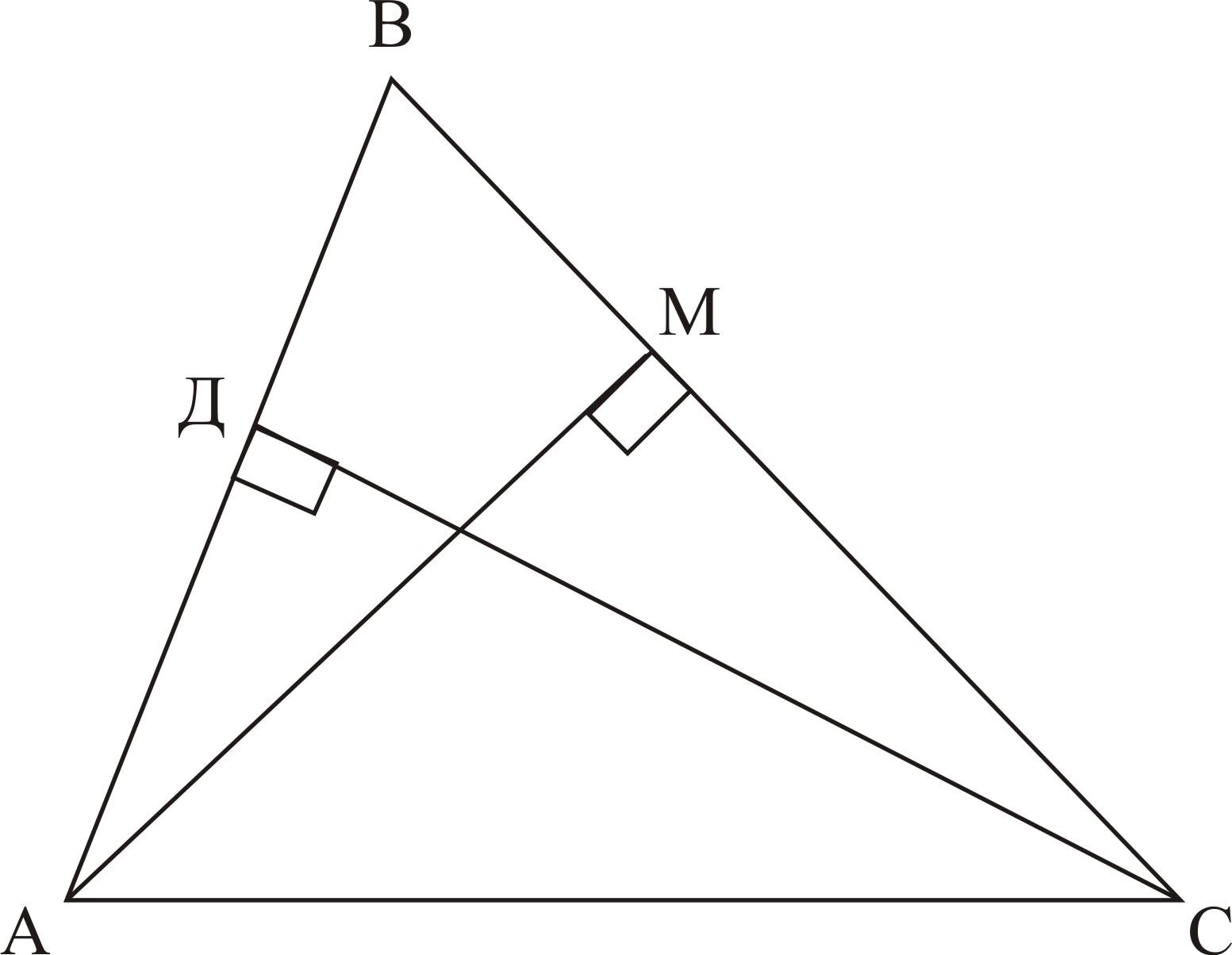 . Проведем высоту АК
. Проведем высоту АК
2.Рассмотрим ΔДАК: Д=30о . Значит, АК=4см (свойство прямоугольного треугольника)
3. SАВСД=1/2▪(2+10)▪4=24см2
Ответ: 24 см2
Учитель: Задачу №469 решите, пожалуйста, самостоятельно. Свое решение можно будет сверить с верным (заранее верное решение
записано на доске).
Дано:
ΔАВС, АВ=16см, ВС=22см, АМ и СД — высоты ΔАВС, СД=11см
Найти: АМ
Решение:
S∆АВС=1/2АВ▪СД=1/2▪16▪11=88см2.
С другой стороны, S∆АВС=1,2ВС▪АМ
Значит, 88=1,2▪22▪АМ, АМ=8см
Ответ: 8см
IV. Самостоятельная работа
Учащиеся работают с тестами (Приложение 1, Приложение 2) и по окончании работы сдают учителю на проверку.
Ответы к тесту
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| I в. | б | в | а | в | б | б | а | в |
| II в. | в | б | в | а | б | б | а | в |
№9 (I в.)
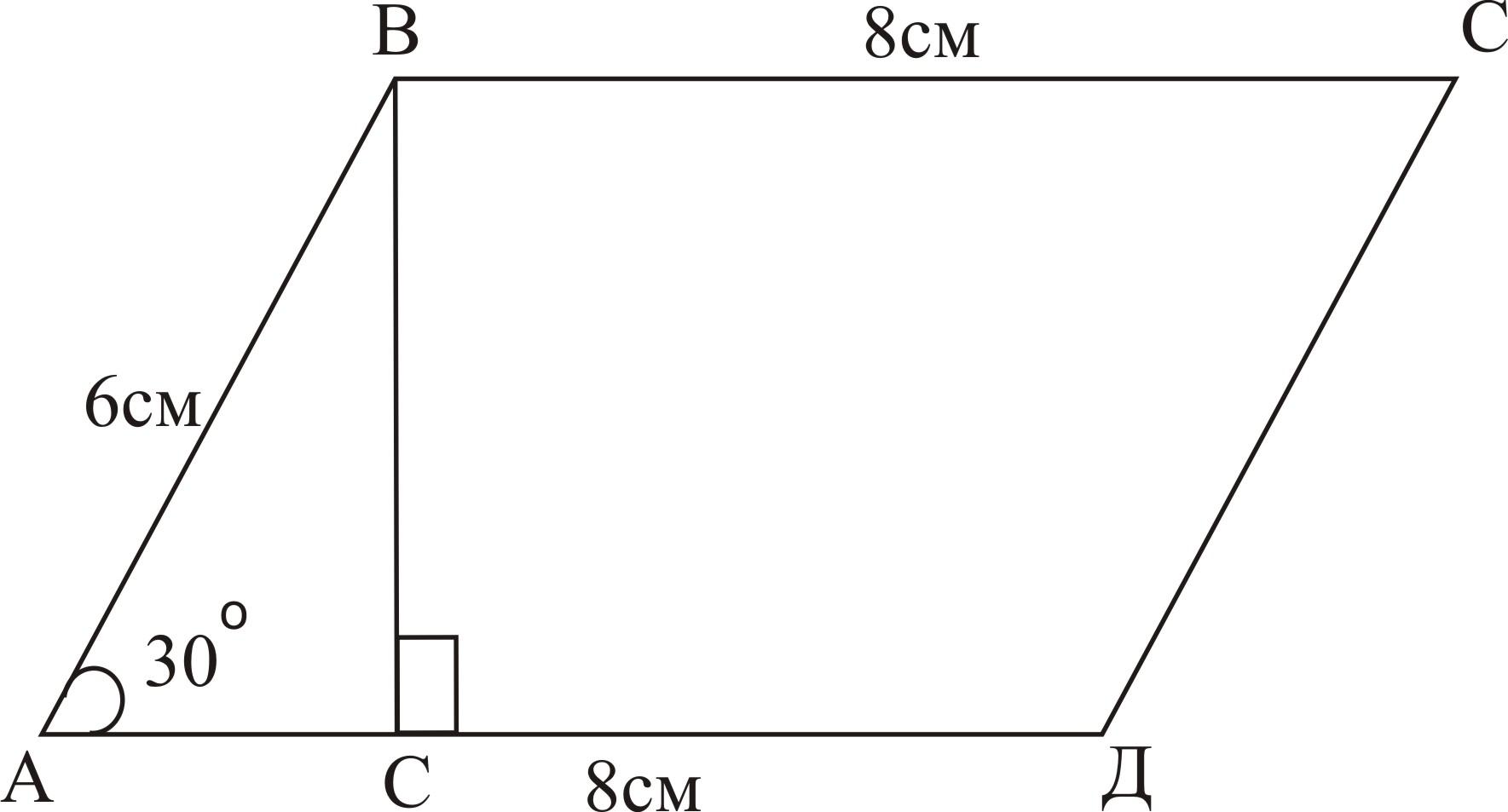 Дано:
Дано:
АВСД — параллелограмм
АВ=6см, АД=8см, А=30о
Решение:
1. Проведем высоту ВК.
2. Рассмотрим ΔАВК — прямоугольный, А=30о, ВК=1/2АВ=3см (по свойству прямоугольного треугольника), ВС=АД=8см (по свойству параллелограмма)
3. Значит, SАВС=3▪8=24см2
Ответ: 24см2
№9 (II в.)
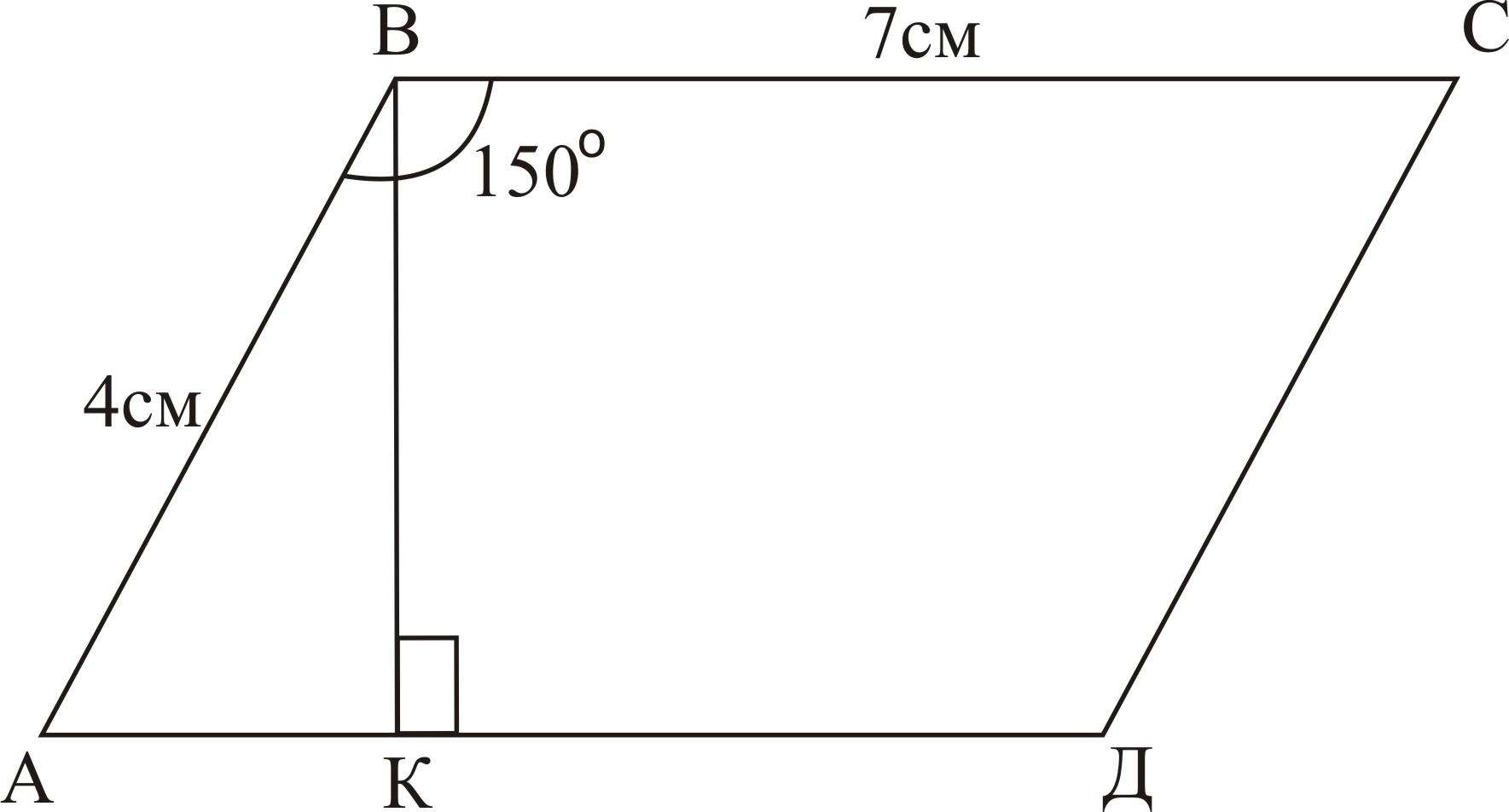 Дано:
Дано:
АВСД — параллелограмм
АВ=4см, ВС=7см
В=170о
Найти: SАВСД
Решение:
1. А=30о, т.к. А и В — односторонние углы при параллельных прямых АД и ВС и секущей АВ.
2. Проведем высоту ВК.
3. Рассмотрим ΔАВК — прямоугольный, А=30о. Значит, ВК=1/2АВ=2см (по свойству равнобедренного треугольника).
АД=ВС=7см (как противоположные стороны параллелограмма)
SАВСД=АД▪ВК=7▪2=14см2
Ответ: 14см2
IV. Подведение итогов урока.
Оценить работу учащихся
Домашнее задание: п. 52, 53; №466, 467, 476 (б).
Учитель: Урок окончен! До свидания!
 айдите площади фигур.
айдите площади фигур.

 ) АС=15см
) АС=15см  ) АВ=10см
) АВ=10см Дано:
Дано: . Проведем высоту АК
. Проведем высоту АК Дано:
Дано: Дано:
Дано: 















