Урок геометрии в 8-м классе с применением ИКТ.
Тема " Площади фигур"
Цель урока: обобщение и систематизация знаний учащихся по теме. Знание учащимися свойств известных им фигур и умение находить площади этих фигур
Задачи:
обучающие:
-привести в систему теоретические знания по теме “Четырехугольники и их площади”;
-закрепить навыки решения задач по данной теме;
развивающие:
-развивать мыслительные операции (проведение аналогии, анализ, синтез);
-развивать пространственное мышление; память, внимание
-развивать логическое мышление.
воспитывающие:
-развивать чувство коллективизма, умение работать в группах, выслушивать ответы одноклассников, оценивать свою работу и работу товарищей;
-прививать интерес к предмету.
Оборудование урока:
компьютеры (класс-комплект),
видеопроектор,
доска,
презентация к уроку
раздаточный материал:
карточки с задачами; геометрические фигуры
компьютерный тест по теме « Четырехугольники и их свойства»
ХОД УРОКА
I. Вводно- мотивационный момент.
“Дорогие ребята! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы тот, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни”.
2. Целеполагание. Учитель озвучивает тему и цель урока.
3. Планирование. Урок пройдет в 3этапа:
1. Входное компьютерное тестирование по теории темы “Четырёхугольники”.
2. Повторение основных положений теории по теме “Площади плоских фигур”.
3. Практическая работа по решению задач в группах
II. Основная часть
1-й этап
Начнем наш урок с выполнения тестового задания по теме « Четырехугольники и их свойства ».Проверим , насколько хорошо вы помните свойства фигур и умеете их применять .( Приложение 1)
На выполнение теста вам дается 5 мин . результаты тестирования выставляются в свой маршрутный лист каждым учащимся . Проводится краткий анализ результатов учителем.
2 этап
Я предлагаю вам послушать стихи и определить, о каких четырехугольниках идет речь?
Определить какими свойствами обладают эти четырехугольники?
Вспомнить основные теоремы, присущие каждой из фигур.
Знаете ли вы меня
Хочу проверить.
Любую площадь я могу измерить,
Ведь у меня 4 стороны
И все между собой равны.
У меня равны еще диагонали,
Углы мне они делят пополам, и , или
На части равные разбит я сам. ( Квадрат)
И у меня равны диагонали,
хочу сказать я ,
хоть меня и не называли.
И хоть я не зовусь квадратом,
он мне приходиться родным братом. ( прямоугольник).
Хоть стороны мои попарно и равны, но не равны мои диагонали.
Да и углы они не делят пополам.
Но все ж , скажи, дружок, кто я? ( параллелограмм).
Мои хотя и не равны диагонали
По значимости всем я уступлю едва ли.
Ведь под прямым углом они пересекаются,
И каждый угол делят пополам.
И очень важная фигура я, скажу я вам.( Ромб)
Геометрический диктант.
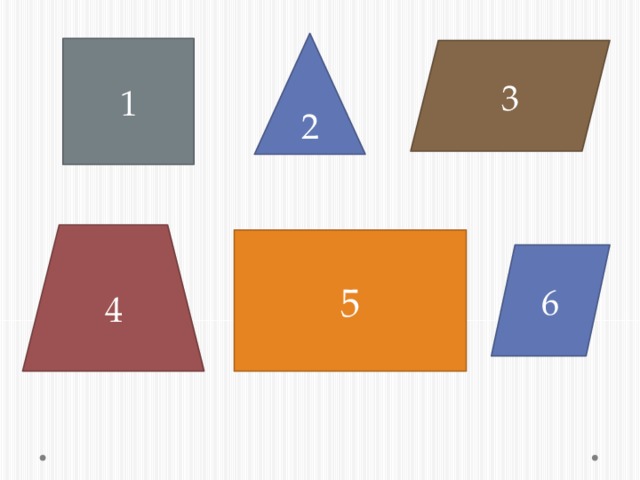
На доске изображены фигуры. Вам необходимо , отвечая на вопросы диктанта, написать номер фигуры, обладающей данным свойством. Затем мы проверим, как хорошо вы знаете свойства данных фигур.
- У какой из фигур диагонали, пересекаясь, делятся пополам?
- У какой из фигур диагонали равны?
- У какой из фигур диагонали делят углы пополам?
- У какой из фигур диагонали перпендикулярны?
- У какой из фигур диагонали перпендикулярны и равны?
- У какой из фигур равны противолежащие углы?
- У какой из фигур все углы равны?
- У какой из фигур равны углы , прилежащие к одной стороне?
- У какой из фигур параллельна пара противолежащих сторон?
- У какой из фигур средняя линия равна половине третьей стороны?
- У какой из фигур средняя линия равна полу сумме оснований?
По окончании диктанта проводится взаимопроверка . ( правильные ответы выведены на доске).Слайд №3. Результаты – количество прав. ответов –выставляется в маршрутный лист
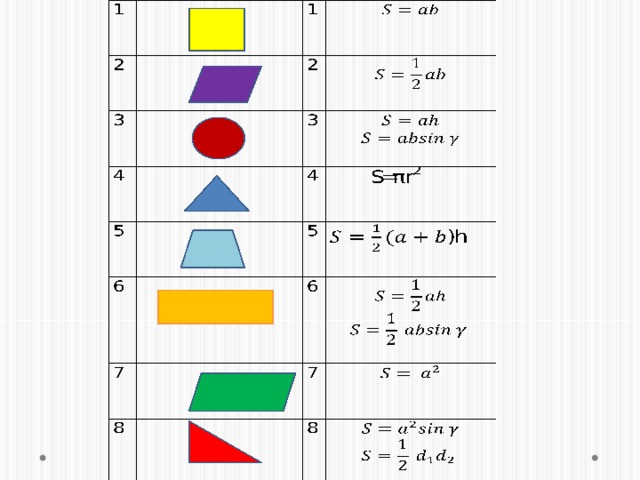
Повторение формул площадей фигур. Задание «Установи соответствие» Слайд №4.
По окончании задания вновь проводится взаимопроверка . ( правильные ответы выведены на доске).Слайд №5
Результаты – количество прав. ответов –выставляется в маршрутный лист
А знаете ли вы , что в школе Пифагора существовали следующие заповеди
- Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.
- Не делай никогда того, чего не знаешь.
- Но научись всему, что следует знать...
-Не пренебрегай здоровьем своего тела…
- Приучайся жить просто и без роскоши
- Не закрывай глаза, когда хочется спать, не разобравши всех своих поступков в прошлый день.
- Помогай не тому, кто ношу сваливает, а тому, кто её взваливает.
Как вы их понимаете?
Задание « Собери формулу».. На магнитной доске расположены отдельные фрагменты формул. Необходимо собрать правильные формулу и объяснить площади каких фигур по ней можно найти и что означает каждая переменная в формуле.
Дополнительная работа в группах. До начала урока учитель разбивает класс на три группы , примерно одинаковой « силы». По команде учителя дети занимают вои места для работы в группах. Каждая группа выбирает спикера, который будет собирать возможные идеи и решения, распределять задания и выступать от имени группы с готовыми решениями.
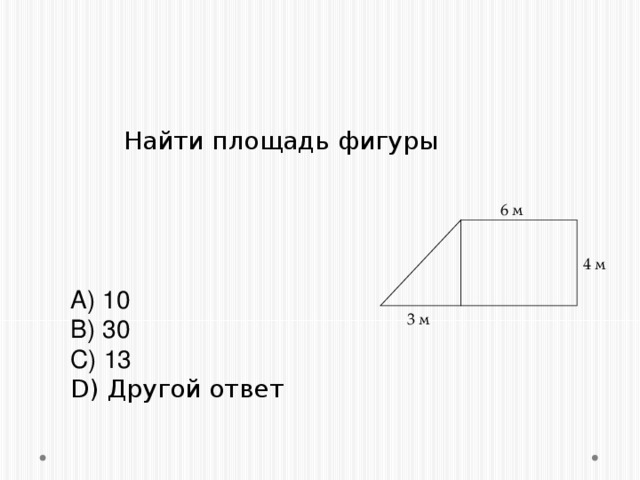
- Задание. На магнитной доске закреплены фигуры, площади которых необходимо найти, выполнив необходимые измерения. Спикер каждой группы выбирает себе задание и по команде учителя группы начинают выполнять задачу ( 3 мин)
- На слайде № 7 изображен чертеж. Каждой команде необходимо найти площадь заданной фигуры( 5-7 мин)
- Площадь параллелограмма ABCD;
- Площадь треугольника CNK;
- Площадь треугольника DCK;
- Площадь трапеции ABCN;
- Площадь прямоугольника MBCN;
- Площадь трапеции ABCK;
Блиц- игра. Устное решение задач по готовым чертежам.
Какая команда наберет больше баллов. За каждый правильный ответ присуждается 1 балл. Слайды №.8-16
Учитель проверяет решения, определяет победителей, а группах учащиеся выставляют каждому баллы (0-5 б) за участие в совместной работе. Эти баллы каждый ребенок ставит в свой оценочный лист.
III. Итоги урока
Подведение итогов. Выставляется средняя оценка. Суммируются результаты за каждый этап урока и эта сумма делится на количество этапов Выставление отметок.
Рефлексия. Чему вы научились сегодня на уроке?
Какими понятиями формулами воспользовались при решении задач?
Что понравилось на уроке? А что не очень?
Домашнее задание: выполнить тест ( уровень- по выбору учащихся) по теме « Площади фигур».
Уровень А.
1 вариант.
- Вычислить площадь прямоугольника со сторонами 3 и 5 см.
А) 30 кв.см; б) 8 кв.см.; в) 15 кв.см.; г) не знаю.
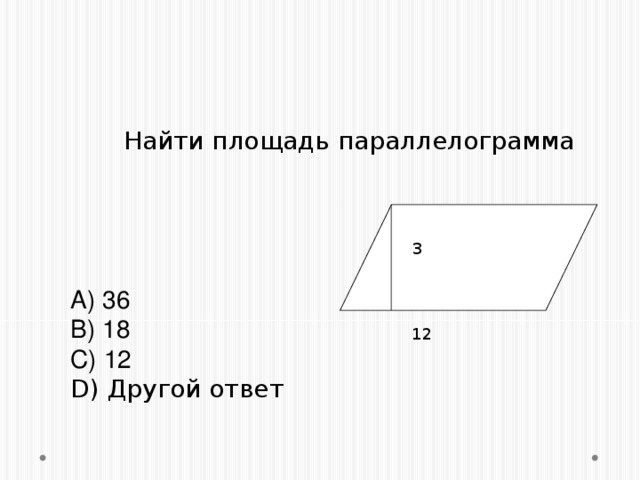
2. Вычислить площадь параллелограмма, еслиодна из его сторон 8 дм, высота , проведенная к этой стороне, равна 6 дм.
А) 24 квдм; б) 48 кв.дм. в) 64 кв.дм. г) нет правильного ответа.
3. Найти площадь квадрата, если его периметр равен 36 см.
А) 81кв.см; б) 18 кв.см.; в) 30кв.см.; г) 36 кв.см.
4. Меньшая сторона прямоугольника равна 6 см, а вторая – на 2 см больше Чему равна площадь прямоугольника?
А) 60 кв.см; б)48 кв.см.; в) 24кв.см.; г) нет правильного ответа
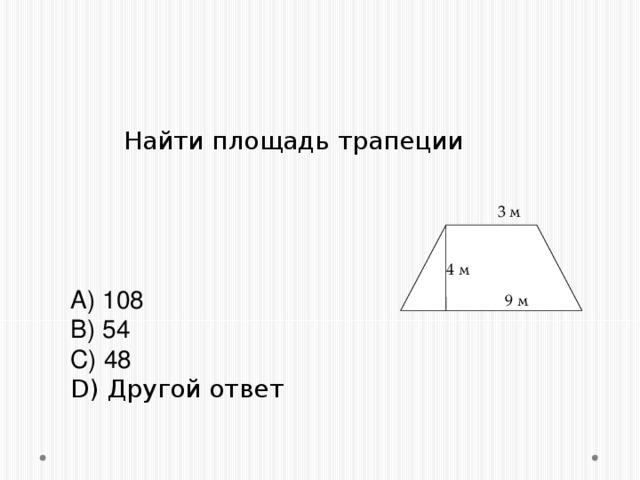
5. Средняя линия трапеции равна 3 см, высота -9 см. Вычислить площадь трапеции.
А) 54кв.см; б)27 кв.см.; в)12кв.см.; г) нет правильного ответа.
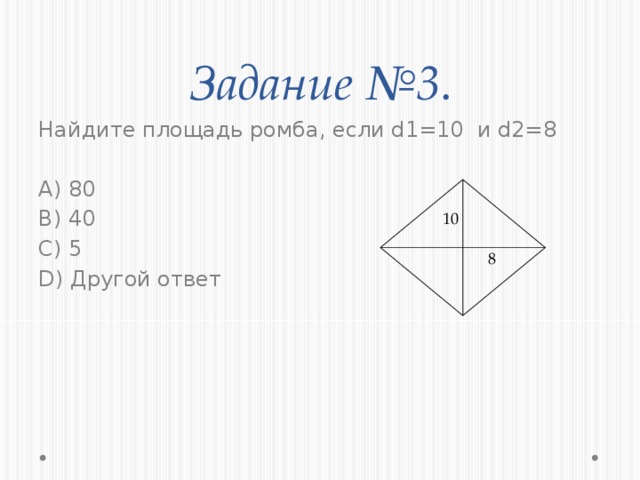
6. Найти площадь ромба, если его диагонали 6 и 8 см.
А) 48кв.см; б)42 кв.см.; в) 24кв.см.; г) нет правильного ответа.
7. Высота треугольника 8 дм, основание 12 дм. Найти площадь треугольника.
А) 60 кв.дм; б)48 кв.дм.; в)1 20 кв.дм.; г) нет правильного ответа
8. В трапеции основания равны 8 и 14 см, высота 8 см. Чему равна площадь трапеции?
А) 44кв.см; б)110 кв.см.; в) 88кв.см.; г) нет правильного ответа
Вариант 2
- Вычислить площадь прямоугольника со сторонами 2 и 5 см.
А) 20 кв.см; б) 14кв.см.; в) 10кв.см.; г) не знаю.
2. Вычислить площадь параллелограмма, еслиодна из его сторон 9дм, высота , проведенная к этой стороне, равна 2дм.
А) 9 квдм; б) 18 кв.дм. в) 36 кв.дм. г) нет правильного ответа.
3. Найти площадь квадрата, если его периметр равен 48 см.
А) 64кв.см; б) 144кв.см.; в) 12кв.см.; г) 36 кв.см.
4. Большая сторона прямоугольника равна 12 см, а вторая – на 8 см меньше.Чему равна площадь прямоугольника?
А) 60 кв.см; б)78кв.см.; в) 50кв.см.; г) нет правильного ответа
5. Параллельные стороны трапеции равны 6 и 9 см, высота -4 см. Вычислить площадь трапеции.
А) 15кв.см; б)108кв.см.; в)30 кв.см.; г) нет правильного ответа.
6. Найти площадь ромба, если его диагонали 10 и 12 см.
А) 120кв.см; б)60кв.см.; в) 24кв.см.; г) нет правильного ответа.
7. Высота треугольника 5дм, основание 12 дм. Найти площадь треугольника.
А) 120 кв.дм; б)65кв.дм.; в)30 кв.дм.; г) нет правильного ответа
8. В трапеции основания равны 15 и 7 см, высота 4 см. Чему равна площадь трапеции?
А) 28кв.см; б)44кв.см.; в) 88кв.см.; г) нет правильного ответа
Уровень В.( открытый)
- Вычислить площадь треугольника, если гипотенуза его равна 12 см, а катет -8 см.
- Вычислить площадь треугольника, если его стороны равны 10 см,12 см,14 см.
- Вычислить площадь ромба, если сторона его равна 12 см , а один из углов – 45?.
- Вычислить площадь квадрата, если его диагональ равна 16 см.
- Вычислить площадь треугольника, стороны которого равны 16 и 9 см, а угол между ними 60?.
- Вычислить площадь параллелограмма, диагонали которого равны 12 и 16 см, а угол между ними равен 30?.
Уровень С( открытый).
- Найти площадь прямоугольной трапеции, если меньшее основание равно 12 см, а боковая сторона – 6 см и угол при основании равен 45?.
- Вычислить площадь ромба, высота которого , а острый угол в 2 раза меньше тупого.
- Найти высоту параллелограмма, если основание на 1 см больше высоты, а площадь равна 20 кв. см
- Найти площадь параллелограмма АВСД, если угол А = 150?, АВ= 3 см, АД= 6 см.
- Острый угол параллелограмма равен 30, а высоты, проведенные из вершины тупого угла, равны 4см и 3см. Найдите площадь этого параллелограмма.
Просмотр содержимого документа
«Пояснительная записка по уроку»
Пояснительная записка по уроку.
Сценарий урока представлен по естественно-научному направлению. Урок геометрии в 8 классе по теме « Площади фигур» с применением ИКТ. Урок проводился по окончании изучения данной темы как повторительно-обобщающий, урок – подготовка к контрольной работе.
Данный урок проводился в классе , более половины из 19 учащихся имеют хороший уровень сформированности общеучебных умений и навыков. Есть дети с ярко выраженными способностями, есть очень старательные . Дети любят преодолевать трудности. Им интересны творческие задания. Развита зрительная память, очень эмоциональны, активны.
Тип урока: урок обобщения и систематизации знаний.Вид урока-урок-повторение.Методы и приемы: репродуктивные (беседа, объяснение), частично- поисковые, практические .
Применяемые технологии: здоровье сберегающие, технология сотрудничества, игровая технология, групповые способы обучения, тестовые технологии.
Оборудование урока:
компьютеры (класс-комплект),видеопроектор, магнитная доска,
презентация к уроку,раздаточный материал:карточки с задачами; геометрические фигуры, листы с формулами, оценочные листы
компьютерный тест по теме « Четырехугольники и их свойства»
Этапы урока:
1. Входное компьютерное тестирование по теории темы “Четырёхугольники”.
2. Повторение основных положений теории по теме “Площади плоских фигур”.
3. Практическая работа по решению задач в группах.
4. подведение итогов урока. Рефлексия.
Каждый этап урока продуман и имеет определенное значение и логически связан с остальными.Подготовка к восприятию: очень большое значение на уроке имеет оргмомент. От эмоций и настроения, переданных детям приветственным словом, они дальше воспринимают настрой учителя на работу.
Нового материала не было , но при повторении тем соблюдался принцип от простого к сложному, от общего к частному.
Использованы различные формы повторении изученного .Этап решения задач развивает творчество, логическое мышление. В процессе решения задач дети выстраивают математическую модель, используя исходные данные.Этап из истории геометрии воспитывает интерес к изучению геометрии, развивает мыслительную деятельность. Урок был выстроен оптимально, он полностью соответствовал моим интересам, темпераменту, уровню подготовки учащихся, соответствовал специфике класса. Психологическая атмосфера была доброжелательной, заинтересованной.
Методической особенностью урока , обеспечивающей его эффективность, является тот момент, что на уроке активно используются многие формы учебной деятельности. При наличии всех этих форм реализуется общая цель, происходит объединение учителя и учеников для ее достижения. Такой урок позволяет решить конкретные дидактические задачи. Задания, предлагаемые учащимся, способствуют обучению учеников самоконтролю. В этом случае контролирующие действия проводят сами ученики путем сверки ответов и образцов решения. ИКТ используется на всех этапах урока как средство наглядности вместе со словом, т.е. словесные и наглядные методы выступают в дидактическом единстве. Наглядный материал оформлен в виде раздаточного материала и в виде презентации.Презентацияиспользуется на различных этапах урока, позволяет систематизировать теоретические знания в игровой форме, а также дает возможность проведения устной работы на уроке, экономию времени для выполнения чертежей к задачам. Компьютерный тест – нестандартная форма проверочной работы по геометрии, проводится в первой половине урока с целью проверки уровня знаний учащихся на начало урока.
Просмотр содержимого документа
«урок геометрии в 8 кл по теме площади фигур»
Урок геометрии в 8-м классе с применением ИКТ.
Тема " Площади фигур"
Цель урока: обобщение и систематизация знаний учащихся по теме . Знание учащимися свойств известных им фигур и умение находить площади этих фигур
Задачи:
обучающие:
-привести в систему теоретические знания по теме “Четырехугольники и их площади”;
-закрепить навыки решения задач по данной теме;
развивающие:
-развивать мыслительные операции (проведение аналогии, анализ, синтез);
-развивать пространственное мышление; память, внимание
-развивать логическое мышление.
воспитывающие:
-развивать чувство коллективизма, умение работать в группах, выслушивать ответы одноклассников, оценивать свою работу и работу товарищей;
-прививать интерес к предмету.
Оборудование урока:
компьютеры (класс-комплект),
видеопроектор,
доска,
презентация к уроку
раздаточный материал:
карточки с задачами; геометрические фигуры
компьютерный тест по теме « Четырехугольники и их свойства»
ХОД УРОКА
I. Вводно- мотивационный момент.
“Дорогие ребята! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы тот, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что геометрия – интересный и нужный предмет.
Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни”.
2. Целеполагание. Учитель озвучивает тему и цель урока.
3. Планирование. Урок пройдет в 3 этапа:
1. Входное компьютерное тестирование по теории темы “Четырёхугольники”.
2. Повторение основных положений теории по теме “Площади плоских фигур”.
3. Практическая работа по решению задач в группах
II. Основная часть
1-й этап
Начнем наш урок с выполнения тестового задания по теме « Четырехугольники и их свойства ».Проверим , насколько хорошо вы помните свойства фигур и умеете их применять . ( Приложение 1)
На выполнение теста вам дается 5 мин . результаты тестирования выставляются в свой маршрутный лист каждым учащимся . Проводится краткий анализ результатов учителем.
2 этап
Я предлагаю вам послушать стихи и определить , о каких четырехугольниках идет речь?
Определить какими свойствами обладают эти четырехугольники?
Вспомнить основные теоремы, присущие каждой из фигур.
Знаете ли вы меня
Хочу проверить.
Любую площадь я могу измерить,
Ведь у меня 4 стороны
И все между собой равны.
У меня равны еще диагонали,
Углы мне они делят пополам, и , или
На части равные разбит я сам. ( Квадрат)
И у меня равны диагонали,
хочу сказать я ,
хоть меня и не называли.
И хоть я не зовусь квадратом,
он мне приходиться родным братом. ( прямоугольник).
Хоть стороны мои попарно и равны, но не равны мои диагонали.
Да и углы они не делят пополам.
Но все ж , скажи, дружок, кто я? ( параллелограмм).
Мои хотя и не равны диагонали
По значимости всем я уступлю едва ли.
Ведь под прямым углом они пересекаются,
И каждый угол делят пополам.
И очень важная фигура я, скажу я вам.( Ромб)
Геометрический диктант.
На доске изображены фигуры. Вам необходимо , отвечая на вопросы диктанта, написать номер фигуры, обладающей данным свойством. Затем мы проверим, как хорошо вы знаете свойства данных фигур.
У какой из фигур диагонали, пересекаясь, делятся пополам?
У какой из фигур диагонали равны?
У какой из фигур диагонали делят углы пополам?
У какой из фигур диагонали перпендикулярны?
У какой из фигур диагонали перпендикулярны и равны?
У какой из фигур равны противолежащие углы?
У какой из фигур все углы равны?
У какой из фигур равны углы , прилежащие к одной стороне?
У какой из фигур параллельна пара противолежащих сторон?
У какой из фигур средняя линия равна половине третьей стороны?
У какой из фигур средняя линия равна полу сумме оснований?
По окончании диктанта проводится взаимопроверка . ( правильные ответы выведены на доске).Слайд № 3. Результаты – количество прав. ответов –выставляется в маршрутный лист
Повторение формул площадей фигур. Задание «Установи соответствие» Слайд №4.
| 1 | 
| 1 | 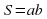
|
| 2 | 
| 2 | 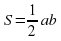
|
| 3 | 
| 3 | 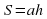
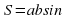
|
| 4 | 
| 4 | S=πr2 |
| 5 | 
| 5 | 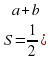 )h )h
|
| 6 | 
| 6 | 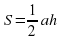
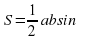
|
| 7 | 
| 7 | 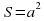
|
| 8 | 
| 8 | 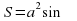
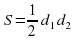
|
По окончании задания вновь проводится взаимопроверка . ( правильные ответы выведены на доске).Слайд №5
Результаты – количество прав. ответов –выставляется в маршрутный лист
А знаете ли вы , что в школе Пифагора существовали следующие заповеди
- Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.
- Не делай никогда того, чего не знаешь.
- Но научись всему, что следует знать...
-Не пренебрегай здоровьем своего тела…
- Приучайся жить просто и без роскоши
- Не закрывай глаза, когда хочется спать, не разобравши всех своих поступков в прошлый день.
- Помогай не тому, кто ношу сваливает, а тому, кто её взваливает.
Как вы их понимаете?
Задание « Собери формулу».. На магнитной доске расположены отдельные фрагменты формул. Необходимо собрать правильные формулу и объяснить площади каких фигур по ней можно найти и что означает каждая переменная в формуле. 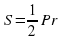
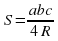
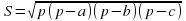
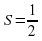 d1 d2 sin α
d1 d2 sin α
3 этап
Практическая работа в группах. До начала урока учитель разбивает класс на три группы , примерно одинаковой « силы». По команде учителя дети занимают вои места для работы в группах. Каждая группа выбирает спикера, который будет собирать возможные идеи и решения, распределять задания и выступать от имени группы с готовыми решениями.
Задание. На магнитной доске закреплены фигуры, площади которых необходимо найти, выполнив необходимые измерения. Спикер каждой группы выбирает себе задание и по команде учителя группы начинают выполнять задачу ( 3 мин)
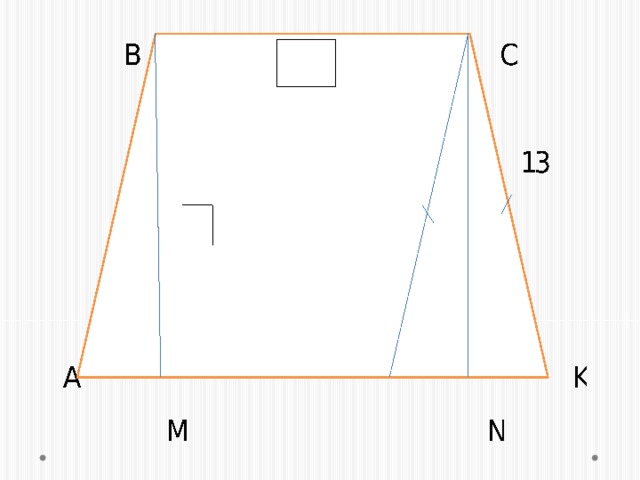
На слайде № 7 изображен чертеж. Каждой команде необходимо найти площадь заданной фигуры ( 5-7 мин)
![]()


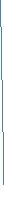

 В В 2424 С
В В 2424 С 24
13
5
А K
M N
Площадь параллелограмма ABCD;
Площадь треугольника CNK;
Площадь треугольника DCK;
Площадь трапеции ABCN;
Площадь прямоугольника MBCN;
Площадь трапеции ABCK;
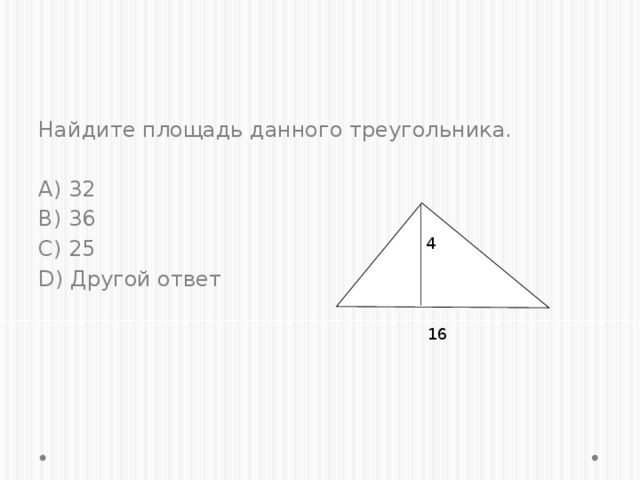
Блиц- игра. Устное решение задач по готовым чертежам.
Какая команда наберет больше баллов. За каждый правильный ответ присуждается 1 балл. Слайды №.8-16
Учитель проверяет решения, определяет победителей, а группах учащиеся выставляют каждому баллы (0-5 б) за участие в совместной работе. Эти баллы каждый ребенок ставит в свой оценочный лист.
III. Итоги урока
Подведение итогов. Выставляется средняя оценка. Суммируются результаты за каждый этап урока и эта сумма делится на количество этапов Выставление отметок.
Рефлексия. Чему вы научились сегодня на уроке?
Какими понятиями формулами воспользовались при решении задач?
Что понравилось на уроке? А что не очень?
Домашнее задание: выполнить тест ( уровень- по выбору учащихся) по теме « Площади фигур».
Уровень А.
1 вариант.
Вычислить площадь прямоугольника со сторонами 3 и 5 см.
А) 30 кв.см; б) 8 кв.см.; в) 15 кв.см.; г) не знаю.
2. Вычислить площадь параллелограмма, еслиодна из его сторон 8 дм, высота , проведенная к этой стороне, равна 6 дм.
А) 24 кв дм; б) 48 кв.дм. в) 64 кв.дм. г) нет правильного ответа.
3. Найти площадь квадрата, если его периметр равен 36 см.
А) 81 кв.см; б) 18 кв.см.; в) 30 кв.см.; г) 36 кв.см.
4. Меньшая сторона прямоугольника равна 6 см, а вторая – на 2 см больше Чему равна площадь прямоугольника?
А) 60 кв.см; б)48 кв.см.; в) 24 кв.см.; г) нет правильного ответа
5. Средняя линия трапеции равна 3 см, высота -9 см. Вычислить площадь трапеции.
А) 54 кв.см; б)27 кв.см.; в)12 кв.см.; г) нет правильного ответа.
6. Найти площадь ромба, если его диагонали 6 и 8 см.
А) 48 кв.см; б)42 кв.см.; в) 24 кв.см.; г) нет правильного ответа.
7. Высота треугольника 8 дм, основание 12 дм. Найти площадь треугольника.
А) 60 кв.дм; б)48 кв.дм.; в)1 20 кв.дм.; г) нет правильного ответа
8. В трапеции основания равны 8 и 14 см, высота 8 см. Чему равна площадь трапеции?
А) 44 кв.см; б)110 кв.см.; в) 88 кв.см.; г) нет правильного ответа
Вариант 2
Вычислить площадь прямоугольника со сторонами 2 и 5 см.
А) 20 кв.см; б) 14 кв.см.; в) 10 кв.см.; г) не знаю.
2. Вычислить площадь параллелограмма, если одна из его сторон 9 дм, высота , проведенная к этой стороне, равна 2 дм.
А) 9 кв дм; б) 18 кв.дм. в) 36 кв.дм. г) нет правильного ответа.
3. Найти площадь квадрата, если его периметр равен 48 см.
А) 64 кв.см; б) 144 кв.см.; в) 12 кв.см.; г) 36 кв.см.
4. Большая сторона прямоугольника равна 12 см, а вторая – на 8 см меньше . Чему равна площадь прямоугольника?
А) 60 кв.см; б)78 кв.см.; в) 50 кв.см.; г) нет правильного ответа
5. Параллельные стороны трапеции равны 6 и 9 см, высота -4 см. Вычислить площадь трапеции.
А) 15 кв.см; б)108 кв.см.; в)30 кв.см.; г) нет правильного ответа.
6. Найти площадь ромба, если его диагонали 10 и 12 см.
А) 120 кв.см; б)60 кв.см.; в) 24 кв.см.; г) нет правильного ответа.
7. Высота треугольника 5 дм, основание 12 дм. Найти площадь треугольника.
А) 120 кв.дм; б)65 кв.дм.; в)30 кв.дм.; г) нет правильного ответа
8. В трапеции основания равны 15 и 7 см, высота 4 см. Чему равна площадь трапеции?
А) 28 кв.см; б)44 кв.см.; в) 88 кв.см.; г) нет правильного ответа
Уровень В. ( открытый)
Вычислить площадь треугольника, если гипотенуза его равна 12 см, а катет -8 см.
Вычислить площадь треугольника, если его стороны равны 10 см,12 см,14 см.
Вычислить площадь ромба, если сторона его равна 12 см , а один из углов – 45⁰.
Вычислить площадь квадрата, если его диагональ равна 16 см.
Вычислить площадь треугольника, стороны которого равны 16 и 9 см, а угол между ними 60⁰.
Вычислить площадь параллелограмма, диагонали которого равны 12 и 16 см, а угол между ними равен 30⁰.
Уровень С ( открытый).
Найти площадь прямоугольной трапеции, если меньшее основание равно 12 см, а боковая сторона – 6 см и угол при основании равен 45◦.
Вычислить площадь ромба, высота которого 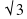 , а острый угол в 2 раза меньше тупого.
, а острый угол в 2 раза меньше тупого.
Найти высоту параллелограмма, если основание на 1 см больше высоты, а площадь равна 20 кв. см
Найти площадь параллелограмма АВСД, если угол А = 150◦, АВ= 3 см, АД= 6 см.
Острый угол параллелограмма равен 30, а высоты, проведенные из вершины тупого угла, равны 4см и 3см. Найдите площадь этого параллелограмма.
Оценочный лист
Ф.И учащегося.------------------------------------------------
|
| Этапы урока | баллы |
| 1. | Тест по теме «Четырехугольники» |
|
| 2. | Геометрический диктант |
|
| 3. | Установи соответствие |
|
| 4. | Собери формулу |
|
| 5. | Работа в группе |
|
|
| итого |
|
|
| оценка за урок |
|

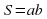

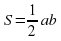

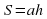
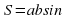


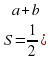

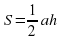
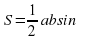

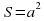

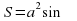
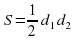
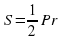
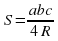
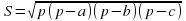
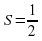



 В В
В В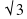 , а острый угол в 2 раза меньше тупого.
, а острый угол в 2 раза меньше тупого.