Конспект урока для учащихся 8 класса в период дистанционного обучения.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока по теме "Описанная окружность"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока по теме "Описанная окружность"»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2050 руб.
2930 руб.
2560 руб.
3650 руб.
2560 руб.
3650 руб.
1970 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

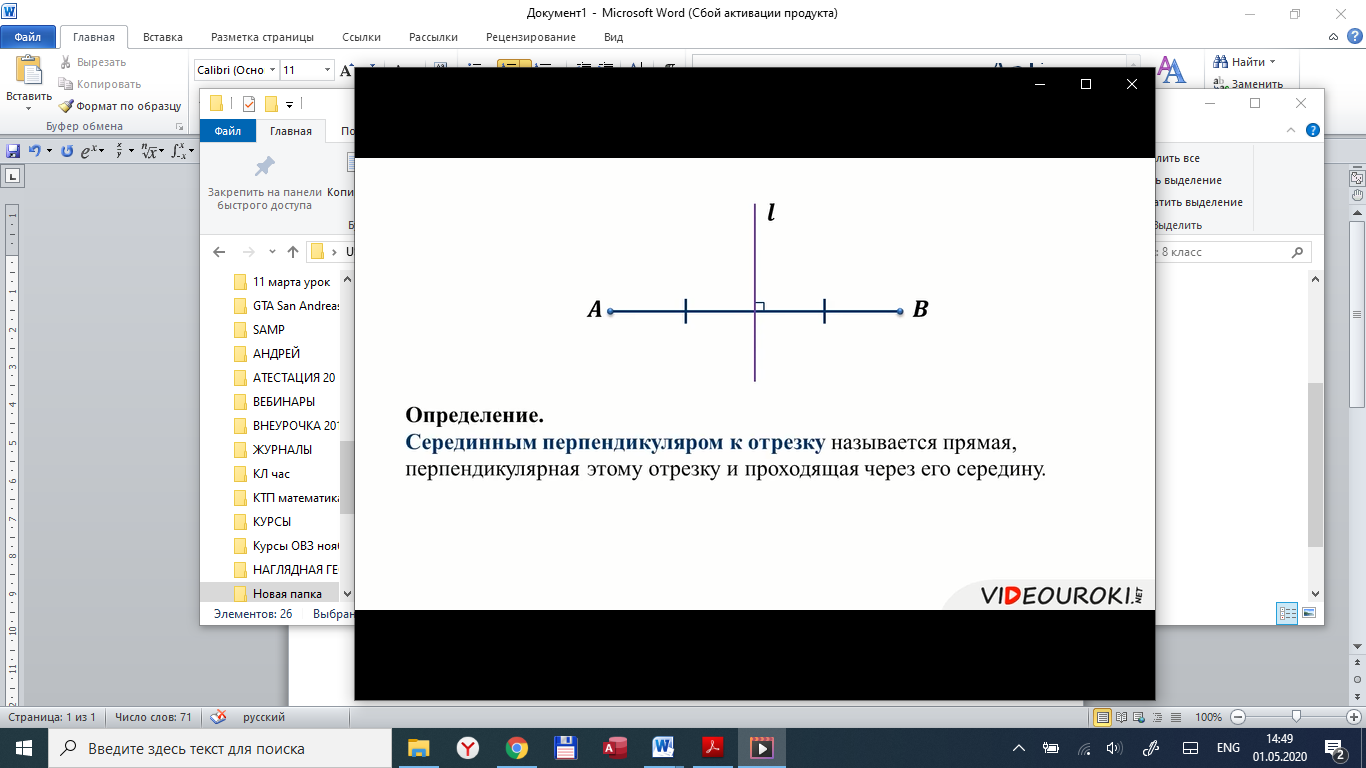
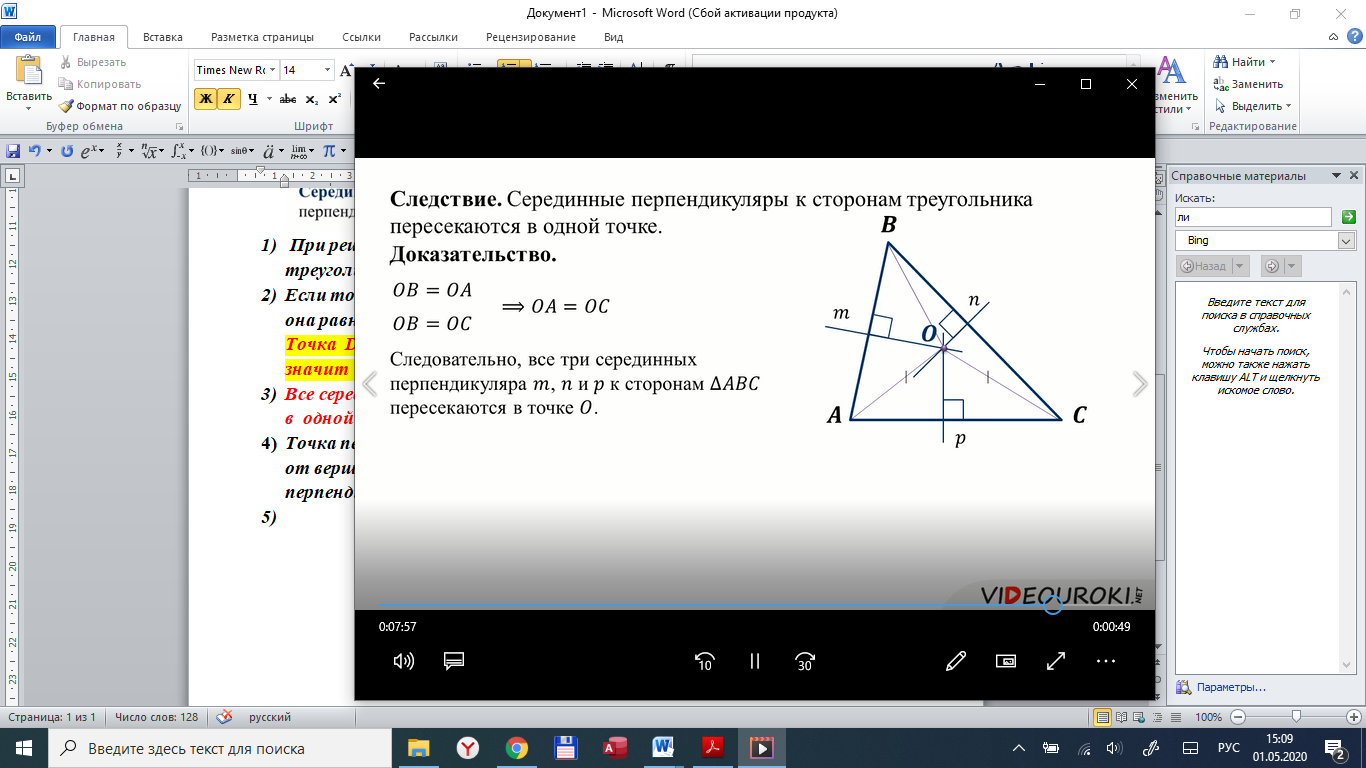 ерединные перпендикуляры не проходят через вершины треугольника !!! (исключение –равносторонний треугольник)
ерединные перпендикуляры не проходят через вершины треугольника !!! (исключение –равносторонний треугольник)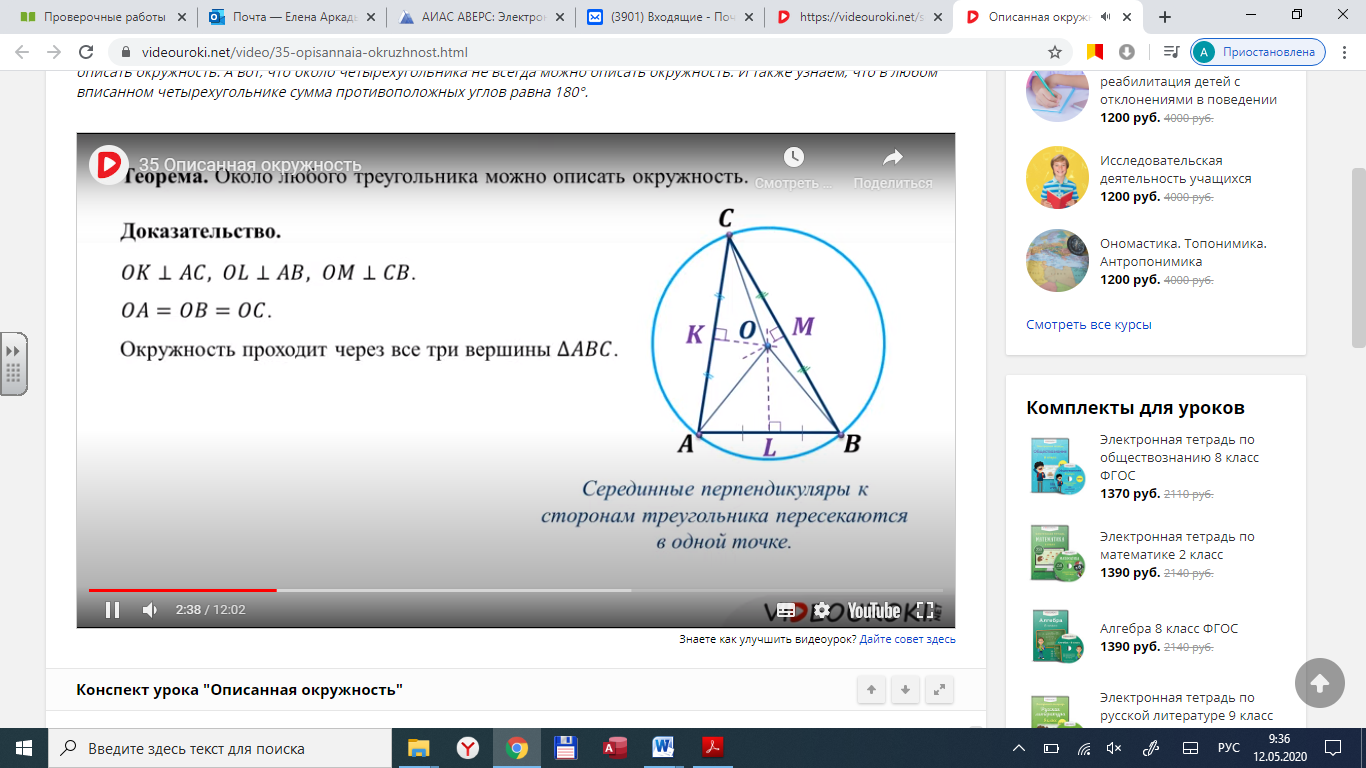 писанная окружность – всегда проходит через все вершины,
писанная окружность – всегда проходит через все вершины, 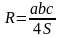 заучиваем наизусть!
заучиваем наизусть! 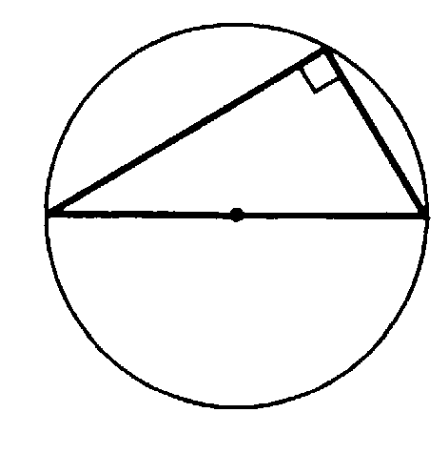 ля прямоугольного треугольника- центр описанной окружности -это середина гипотенузы (вписанный угол опирается на диаметр-прямой).Запомнить!важно для решения задач гипотенуза является диаметром!!!
ля прямоугольного треугольника- центр описанной окружности -это середина гипотенузы (вписанный угол опирается на диаметр-прямой).Запомнить!важно для решения задач гипотенуза является диаметром!!!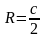 , где c- гипотенуза
, где c- гипотенуза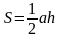
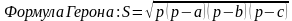
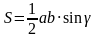 , где
, где 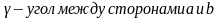
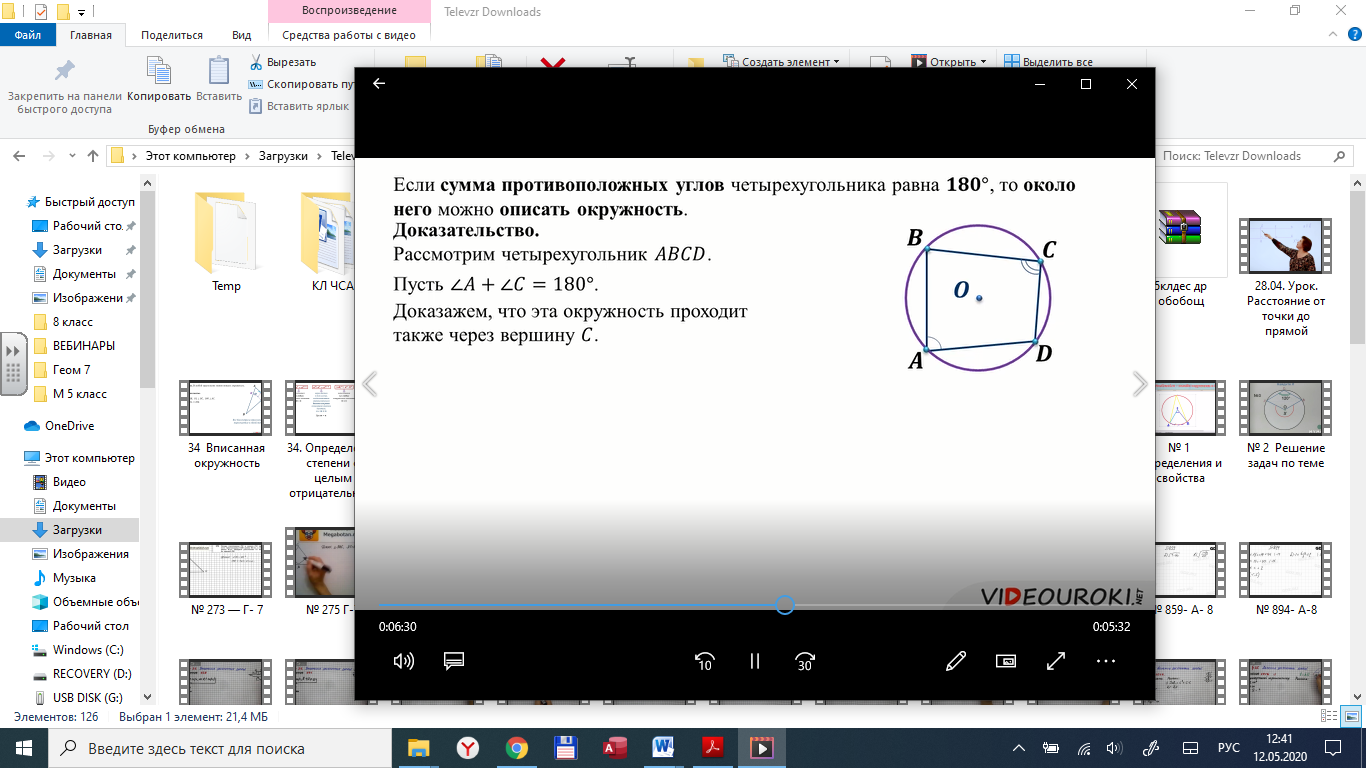 глы треугольника - это углы, вписанные в окружность (их вершины на окружности), значит применяем свойство: вписанный угол равен половине центрального угла или половине дуги, на которую опирается
глы треугольника - это углы, вписанные в окружность (их вершины на окружности), значит применяем свойство: вписанный угол равен половине центрального угла или половине дуги, на которую опирается BD = AB
BD = AB 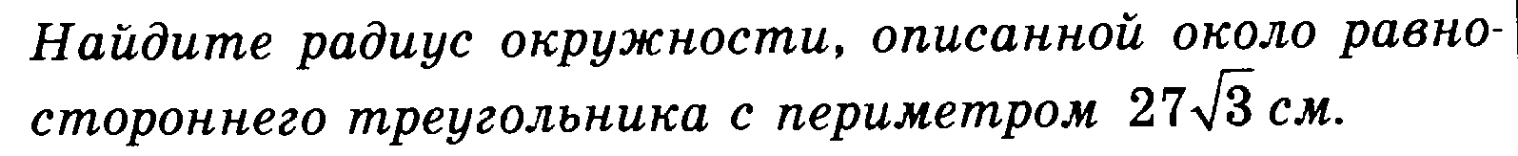
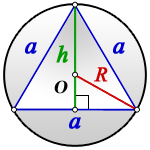 Применяем основную формулу по теме:
Применяем основную формулу по теме: P= 3a , тк стороны равны, значит a =9
P= 3a , тк стороны равны, значит a =9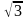
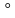 .
.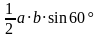 =
= 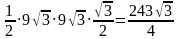
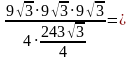 9 Ответ: 9.
9 Ответ: 9.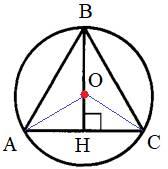 2. Основание равнобедренного треугольника равно 48 см, а высота, проведенная к основанию, равна 32 см. Найдите радиус окружности, описанной около треугольника
2. Основание равнобедренного треугольника равно 48 см, а высота, проведенная к основанию, равна 32 см. Найдите радиус окружности, описанной около треугольника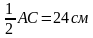
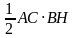 =
= 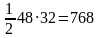
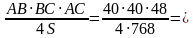 25 Ответ: 25
25 Ответ: 25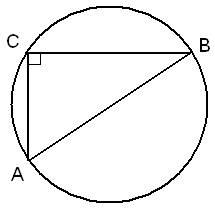 апомнить! Если прямоугольный треугольник вписан в окружность, то гипотенуза является диаметром!
апомнить! Если прямоугольный треугольник вписан в окружность, то гипотенуза является диаметром! 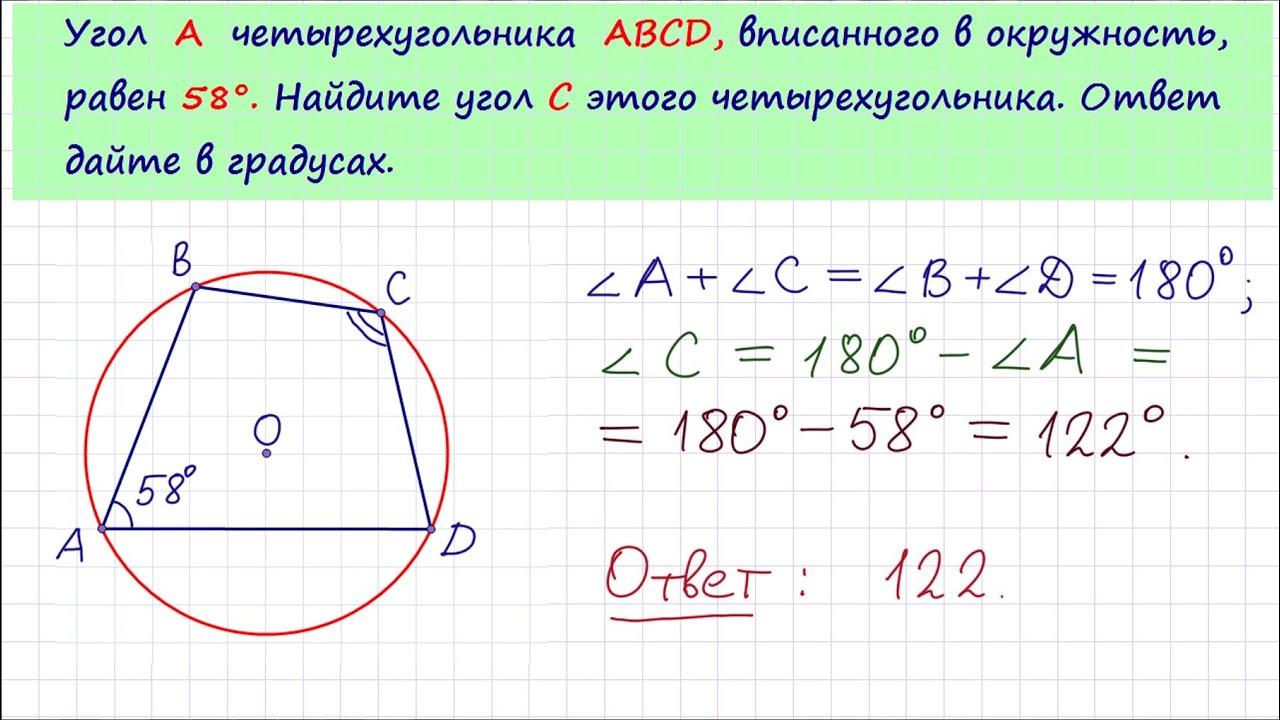 5
5