| Раздел 8.3А Площади | Школа: |
| Дата: | ФИО учителя: |
| Класс: 8 | Количество присутствующих: | отсутствующих: |
| Тема урока | Площадь треугольника. Решение задач. |
| Вид урока | Урок закрепления знаний и формирования умений и навыков вычисления площадей треугольников. |
| Цели обучения | 8.3.3.12 выводить и применять формулы площади треугольника (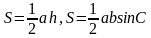 и формула Герона) и формула Герона) |
| Цели урока | -Все учащиеся: Знать формулы для вычисления площади треугольника. - Большинство: Применять формулы для вычисления площадей треугольников при решении задач Некоторые: Применять формулы для вычисления площадей треугольников при решении задач прикладных задач. |
| Критерии оценивания | Учащийся: Знает и применяет формулы для вычисления площади треугольника. Применяет формулы для вычисления площадей треугольников при решении прикладных задач.
|
| Языковые цели
| Учащиеся будут: – формулировать словесно формулы площадей фигур; – формулировать вопросы для проверки понимания формул; – комментировать вывод формул площадей фигур. Учащиеся знают термины, используемые при решении задач на нахождение площадей фигур, (площадь, основание фигуры, высота, длина стороны, периметр, синус угла, диагонали и т.д.) Используя эти термины, учащиеся комментируют ход решения задач, обосновывая свое решение. Серия полезных фраз для диалога/письма для определения площади треугольника/квадрата/прямоугольника/ параллелограмма/ром …. для того, чтобы вычислить площадь треугольника …, необходимо … чтобы применить формулу …, необходимо …; если уменьшить сторону квадрата в k раз …, то площадь …;
|
| Привитие ценностей | Привитие ценностей осуществляется посредством работ, запланированных на данном уроке. Умение учиться, анализировать ситуацию, адаптироваться к новым условиям, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время. |
| Межпредметные связи | Связь с экономикой осуществляется посредством решения прикладных задач. |
| Навыки использования ИКТ | Применение интерактивной доски в качестве демонстрационного средства и средства записи. |
| Предварительные знания
| Знание о величинах, умение переводить величину из одних единиц измерения в другие. Знание определений многоугольника, треугольника, четырехугольника и их элементов. Умение распознавать виды треугольников Умение применять формулы площади квадрата при решении задач. Знать формулы для вычисления площадей треугольников. |
| Ход урока |
| Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы |
| Начало урока 5 мин Стадия вызов | Создание коллаборативной среды В начале урока сделать акценты на: - концентрацию внимания учащихся; - совместно с учащимися определить цели урока/ЦО; - Давайте все вместе попытаемся сформулировать цели нашего урока, чему мы с вами должны научиться? - определить «зону ближайшего развития» учащихся, ожидания к концу урока;. Повторение теоретического материала. Фронтальный опрос по пройденному материалу Стратегия «Математический бой» Ученики задают друг другу вопросы по формулам для вычисления площадей треугольников,. Учащиеся отвечают на вопросы, дополняют друг друга. Демонстрация слайдов с чертежами и формулами способствует зрительному восприятию материала. ФО «Большой палец»
| Презентация слайды 1-5 |
| Середина урока 3 мин
10 мин
10 мин
10 мин | Тест «Мозговой штурм» Учащиеся выполняют задания в парах, обсуждают решение, консультируют друг друга. После выполнения заданий осуществляется взаимопроверка между парами учащихся. Учитель комментирует работу учащихся, помогает при необходимости, показывает правильные решения на доске. ФО «три хлопка» Решение задач стратегия «Карусель» Предоставьте ресурс с четырьмя задачами разной тематики, На первом этапе работы, учащиеся разделяют задания в между собой. Затем объясняют в паре решение своей задачи. Учащиеся комментируют решение задач, по завершению выполнения, учащиеся подводят итоги, учитель предоставляет обратную связь учащимся. Учащиеся проводят самооценивание и взаимооценивание работ по готовым критериям. ФО «Две звезды одно пожелание» Физминутка
Легенда о хане Хан делит треугольный участок земли между двумя сыновьями. Для этого отец вершину треугольника соединяет с срединой противолежащей стороны, т.е строит медиану треугольника.) Учитель предлагает помочь разобраться в проблеме раздела земли. Вопрос-ответ 1. Как вы думаете, над чем задумались сыновья? 2. Поровну ли их отец поделил землю? 3. Почему у сыновей возникли сомнения? 4. Как вы думаете, мы можем проверить поровну ли отец поделил участок? (да, нет) 5. Как это сделать? Следующий этап урока – работа в паре Учитель предлагает учащимся: Проверим гипотезу о равновеликости участков земли. И сделаем вывод. Медиана делит треугольник на два равновеликих треугольника. ФО «Похвала»
Решение прикладной задачи. Фронтальная работа. Учитель совместно с учащимся решает прикладную задачу, используя формулы для нахождения площади треугольника. Решение прикладных задач повышает мотивацию учащихся к изучению математики и способствуют лучшему пониманию изучаемого материала. Домовладельцу необходимо утеплить фронтон дома, имеющий форму равнобедренного треугольника с боковыми сторонами 10м и основанием 12м. Сколько потребуется уплатить строителям, если стоимость работы - 3000 тенге за 1м2? Ответ:144000т |
слайды 6-9
Приложение№1 слайды 10-11
Приложение№2
Слайд 13
Приложение№3 Слайд 13-15
Слайд16 |
| Конец урока 2 мин | В конце урока учащиеся проводят рефлексию: - что узнал, чему научился? - что осталось непонятным? - над чем необходимо работать? -Пригодятся ли нам знания, полученные на уроке? -Какие положительные моменты были на уроке? (обоснуйте свой оптимизм) Домашняя работа. Дифференцированное Творческого характера А если бы у хана было 4 сына? Возможно ли поделить участок треугольной формы на 4 четыре равных по площадям треугольников. Как это сделать?
| Слайды 17-19
Приложение№4 |
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? Более одаренные получат задания повышенной сложности | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
| Здоровье и соблюдение техники безопасности |
| Дифференциация может быть выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в оказании индивидуальной поддержки учащемуся, в подборе учебного материала и ресурсов с учетом индивидуальных способностей учащихся (Теория множественного интеллекта по Гарднеру). Дифференциация может быть использована на любом этапе урока с учетом рационального использования времени. | Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.
| Здоровье сберегающие технологии. Используемые физминутки и активные виды деятельности. Пункты, применяемые из Правил техники безопасности на данном уроке. |
| Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
|
|
| Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
1. В прямоугольном треугольнике катет равен 8 см, а один острый угол имеет меру 450. Найти площадь данного треугольника.
2. Найдите площадь равнобедренного треугольника с основанием 5 см, если угол, противолежащий основанию, равен 600.
3. В треугольнике одна из сторон равна 6 см, а опущенная на нее высота — 8см. Найдите площадь треугольника.
4. Две стороны треугольника равны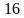 см и 9 см соответственно, а угол между ними 300. Найдите площадь данного треугольника.
см и 9 см соответственно, а угол между ними 300. Найдите площадь данного треугольника.
1. В прямоугольном треугольнике катет равен 8 см, а один острый угол имеет меру 450. Найти площадь данного треугольника.
2. Найдите площадь равнобедренного треугольника с основанием 5 см, если угол, противолежащий основанию, равен 600.
3. В треугольнике одна из сторон равна 6 см, а опущенная на нее высота — 8см. Найдите площадь треугольника.
4. Две стороны треугольника равны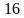 см и 9 см соответственно, а угол между ними 300. Найдите площадь данного треугольника.
см и 9 см соответственно, а угол между ними 300. Найдите площадь данного треугольника.
Дескриптор: Обучающийся - строит чертеж; - определяет алгоритм решения; - выбирает формулу для вычисления площади треугольника; - выполняет вычислительные операции; - находит площадь; - вычисляет сумму оплаты.
Дескриптор: Обучающийся - использует свойство боковых сторон равнобедренного треугольника; - находит боковые стороны равнобедренного треугольника; - применяет формулу для вычисления площади; - выполняет вычислительные операции; - находит площадь треуголь
Цель обучения 8.1.3.12 выводить и применять формулы площади треугольника Критерий оценивания Обучающийся • Решает задачи на нахождение площади треугольника различными способами Уровень мыслительных навыков Применение
Дескриптор: Обучающийся - применяет теорему Пифагора; - находит сторону треугольника; - применяет формулу для вычисления площади треугольника; - находит площадь треугольника.
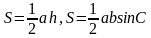 и формула Герона)
и формула Герона)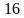 см и 9 см соответственно, а угол между ними 300. Найдите площадь данного треугольника.
см и 9 см соответственно, а угол между ними 300. Найдите площадь данного треугольника. 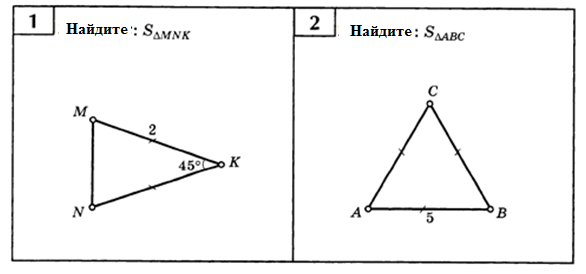
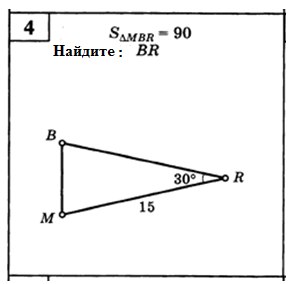
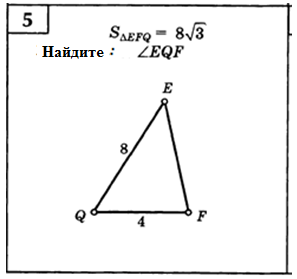
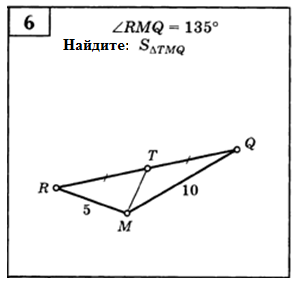
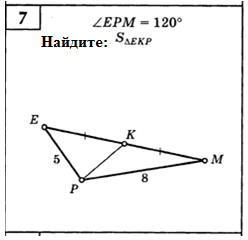
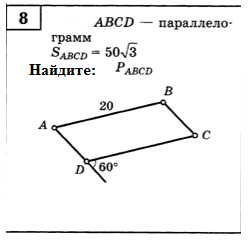
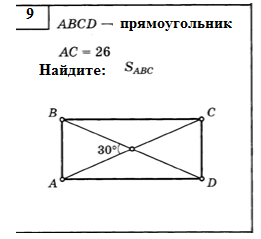
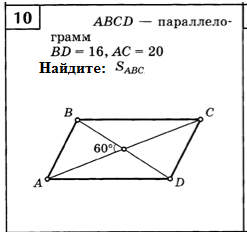
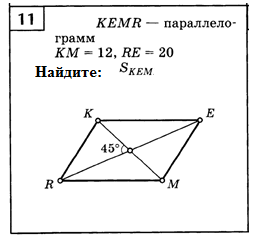 м
м