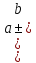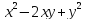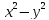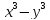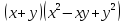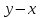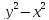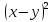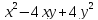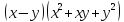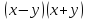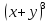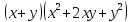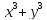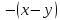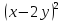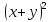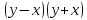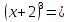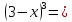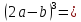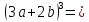| 7.5А Формулы сокращенного умножения | Школа: КГУ ШГ № 118 |
| Дата: 24.01.2018 | ФИО учителя: Липова Н.А. |
| Класс: 7а,б,в,г,д,е | Предмет: | алгебра |
| Тема урока: | Куб суммы и куб разности двух выражений |
| Тип урока | Урок изучения нового материала |
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | Учащийся: 7.2.1.18 знать и применять формулы сокращённого умножения  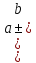 |
| Цели урока | Ознакомить учащихся с формулами «куб разности» и «куб суммы»; Научить применять формулы сокращённого умножения 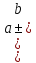 в упрощениях и преобразованиях выражений. в упрощениях и преобразованиях выражений. |
| Критерии оценивания | Учащиеся умеют: знать и применять формулы сокращенного умножения; применять формулы сокращенного умножения при упрощении алгебраических выражений; применять формулы сокращенного умножения при разложении многочлена на множители |
| Языковые цели | давать словесную формулировку формул сокращённого умножения; записывать формулы сокращенного умножения по словесной формулировке; аргументировать выбор способа разложения многочлена на множители; объяснять выполнение разложения многочлена на множители. Лексика и терминология, специфичная для предмета: формулы сокращенного умножения; разность квадратов двух выражений; квадрат суммы двух выражений; квадрат разности двух выражений; разность кубов двух выражений; наибольший общий множитель; куб разности двух выражений; | | Серия полезных фраз для диалога/письма разность квадратов двух выражений равна…; квадрат суммы (разности) двух выражений равен….; куб суммы (разности) двух выражений равен….; сумма (разность) кубов двух выражений равна…; чтобы вынести общий множитель за скобки…; наибольший общий делитель коэффициентов…; данное выражение можно записать в виде…; чтобы разложить многочлен на множители.…; произведение множителей равно нулю, если…; сгруппируем члены многочлена (выражения), имеющие …; чтобы представить данный многочлен в виде произведения, используем …; чтобы в данном выражении выделить квадрат суммы (разности)…. |
| Привитие ценностей | Уважение, сотрудничество, открытость. Привитие ценностей осуществляется посредством/через парную и групповую виды работ. |
| Навыки использования ИКТ | Применение интерактивной доски. |
| Предварительные знания | Умение выполнять действия с одночленами и многочленами. Знание ФСУ квадрат суммы и разности, разность квадратов. |
| Ход урока |
| Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы |
| Начало урока 2 мин | Орг. момент. Приветствие. Создание благоприятного психологического климата в классе. Стратегия «Комплимент». Учащиеся говорят друг другу комплимент. | мяч |
| Актуализация знаний 5 мин | Стратегия «Соответствие». Для каждого выражения из левого столбца подберите ему тождественно равное в правом: | 1 | 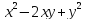
| а | 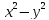
| | 2 | 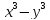
| б | 
| | 3 | 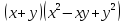
| в | 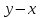
| | 4 | 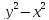
| г | 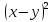
| | 5 | 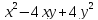
| д | 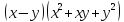
| | 6 | 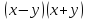
| е | 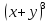
| | 7 | 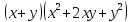 | ж | 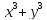
| | 8 | 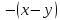
| з | 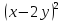
| | 9 | 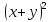
| и | 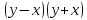
|
Ответы:
Самопроверка по ключу. Ключ: 1г, 2д, 3ж, 4и, 5з, 6а, 7е, 8в, 9б. Рефлексия этапа: Были сложности в выполнении задания? Какие? Все ли пары вы нашли? Какая пара является для Вас новой? Как Вы думаете, формула ли это?
|
Приложение 1 |
| Проблемный вопрос 2 мин | 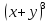 и и 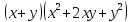
| Пара 7е составляет ли равенство? Можно ли назвать её ФСУ? Почему? | 
|
|
|
| Выход на тему урока 2 мин | 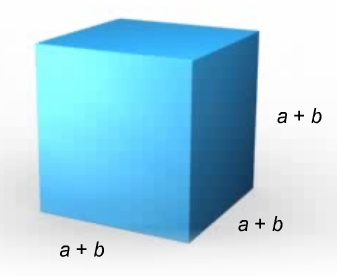 Совместный вывод формулы для объёма куба. Диалоговое обучение. | Приложение 2 |
| Формулировка темы и целей урока 1 мин | Учащиеся формулируют тему урока и его цели. - По выполненным заданиям как вы думаете, что будет являтся предметом нашего исследования на уроке?
|
|
| Самостоятельное изучение нового материалы 10 мин
Мини исследование Вывод ФСУ Куб разности
| Диалоговое обучение. Учитель: Вспомним, как умножить многочлен на многочлен? Ученик: При умножении многочлена на многочлен каждый член одного многочлена умножают на каждый член другого. Учитель: Однако в некоторых случаях умножение многочленов можно выполнить короче, воспользовавшись формулами сокращённого умножения. Учитель: Зная формулы квадрата суммы и квадрата разности, нетрудно вывести формулы куба суммы и куба разности. Именно эти преобразования были выполнены выше.
Работа в группах. Стратегия «Соседи по партам». Учащиеся объединяются в группы по 4 человека по номеру парт (1-2), (3-4), (5-6) и так далее. Самостоятельно докажите ФСУ «куб разности» и сформулируйте устно. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. Защита работы группы.
|
Листы А3, маркеры
|
| Закрепление. 17 мин | Закрепление с попутным обсуждением. Отработка формул. №1. Представить выражение в виде многочлена: a) 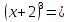 б) 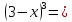 в) 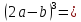 г) 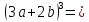 №2. Представьте в виде многочлена: а) (2а2+3в2)3 в) (10х4–6у2)3 №3. Представьте многочлен в виде куба двучлена: а) (8р3–27q3+54pq2–36p2q) в) (х3у3+6х2у2+12ху+8) № 5.111, №5.109 Рефлексия этапа: | Приложение 3
учебник |
| Рефлексия 1 мин
| Учащиеся дополняют следующие предложения: Сегодня я узнал… Было интересно… Было трудно… Я выполнял задания… Теперь я могу… Урок дал мне для жизни… | |
| Домашнее задание 1 мин | Выучить теоретический материал. Уметь выводить ФСУ 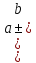 . .
№ 5.100(3 ст), № 5.103 |
Учебник |
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности |
| Дифференциация может быть выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в оказании индивидуальной поддержки учащемуся, в подборе учебного материала и ресурсов с учетом индивидуальных способностей учащихся (Теория множественного интеллекта по Гарднеру). Дифференциация может быть использована на любом этапе урока с учетом рационального использования времени. | Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока. | Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности. Пункты, применяемые из Правил техники безопасности на данном уроке. |
| Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
|
|
| Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках |