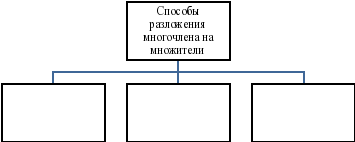
Многочлен, способ группировки, вынесение общего множителя за скобки, формулы сокращенного умножения
| № п/п | Название этапа урока | Деятельность учителя | Деятельность учащихся | Цель этапа | УУД |
-
| Организационный момент. Актуализация знаний. | Приветствие учителя Учитель проводит устную работу, используя интерактивную доску. Учащиеся по желанию выходят к доске и с помощью маркера устанавливают взаимосвязь между выражениями, Вызываются 2-3 ученика. Задание: Стрелками указать связь между выражениями: Вопрос: Какие преобразования мы выполняли с многочленом в этих примерах?
Вопрос: Исходя из ваших действий в примерах, как выдумайте, чем мы сегодня будем заниматься на уроке? Сформулируйте тему сегодняшнего урока? Вопрос: Ребята как вы думаете, какова цель нашего сегодняшнего урока? | Приветствие учащихся
Ответ: раскладывали на множители, выносили общий множитель за скобки, группировали одночлены, входящие в многочлен, использовали формулы разность квадратов, квадрат суммы сокращенного умножения.
Ответ: « Применение различных способов для разложения многочлена на множители»
Ответ: | | Личностные: стимулирование, самоопределяются, настраиваются на урок Познавательные: целеполагание, ставят перед собой цель: «Что я хочу получить сегодня от урока» Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками Регулятивные: перед тем, как начать действовать определяет последовательность действий
|
-
| Мотивация | Вы когда – нибудь слышали кто такие исследователи? Исследователь – человек, занимающийся научными исследованиями. Исследовать – подвергнуть научному изучению. Сегодня мы будем учиться проводить исследование. Любая профессия предполагает постановки цели, выдвижения гипотез. Все учёные – исследователи работают по определенному плану. Итак: Этапы исследования: Актуальность. История вопроса. Теоретическая база. Постановка гипотезы. Доказательство гипотезы. Вывод. Ребята, любое исследование начинается с проблемы.
Вспомним короля математики Карла Гаусса. Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс ( а было ему 10 лет) заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 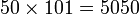 . Математики народ особый, они ищут более рациональные (рациональный, значит разумный) пути решения проблем. Сегодня мы поступим как истинные математики. . Математики народ особый, они ищут более рациональные (рациональный, значит разумный) пути решения проблем. Сегодня мы поступим как истинные математики.
Как вы знаете, в ходе исследования ученые ведут журналы наблюдений. Давайте и мы с вами сегодня тоже будем вести журнал наблюдений. Перед вами на столах заготовки «бортовых журналов». В левую колонку запишите, что вам известно по данной теме?
Какие способы разложения на множители вы знаете. Учитель в это время, выслушав варианты, на интерактивной доске заполняет эту колонку
| Ответ
Вписывают в колонки ответы
Далее дети проговаривают вслух, какие способы они записали.
| | Личностные: осознание ответственности за общее дело Познавательные: поиск и выделение информации, установление причинно-следственных связей, осознанное построение речевого высказывания Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками Регулятивные: перед тем, как начать действовать определяет последовательность действий |
-
| Проблема | Ребята как я вам уже говорила любое исследование начинается с проблемы На доске записано задание: Найти значение многочлена: X6+2 X5+9 X4+16 X3 +24 X2+32 X+16, если X=2. Как нам выполнить это задание? | Незнаем, непосредственным счётом займёт слишком много времени. | Включение учащихся в учебную деятельность Актуализация учебного содержания необходимого и достаточного для восприятия нового материала Актуализация мыслительных операций, необходимых для восприятия нового материала | Личностные: осознание ответственности за общее дело Познавательные: поиск и выделение информации, установление причинно-следственных связей, осознанное построение речевого высказывания Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками Регулятивные: перед тем, как начать действовать определяет последовательность действий |
-
| История вопроса. | У любой проблемы есть своя история. Поэтому обязательным этапом является история вопроса. Чтобы решить эту проблему, мы используем наш опыт. Какие способы вы знаете разложения многочлена на множители? Слушаю ваши ответы и заполняем таблицу | Ответы и заполнение таблицы 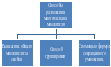
| Актуализация мыслительных операций, необходимых для восприятия нового материала | Коммуникативные Познавательные |
-
| Теоретический материал | Как настоящие исследователи вспомним теорию. У вас на столах есть учебники, воспользуйтесь ими. Подумайте и ответьте на следующие вопросы: 1)Что такое многочлен? 2)Что значит разложить многочлен на множители? 3) Формулы сокращенного умножения. | 1)Многочленом называется сумма одночленов. Ответ 2)Представить многочлен в виде произведения двух или нескольких многочленов или одночленов. Ответ 3)Формулы сокращенного умножения.(Проговорите формулы). a2+ 2аb + b2 = (a + b)2 a2 - 2аb + b2 = (a - b)2 a2 - b2 = (а – b)(а + b) a3+ b3 = (а + b)( a2 - аb + b2) a3- b3= (а - b)( a2+ аb + b2) |
-
| Практика | Теорию мы повторили, сейчас проверим ваши практические навыки разложения многочлена на множители. Следующее задание для группы: разложить на множители каждый многочлен, выбрать ответ и записать соответствующую букву, в итоге у вас получится слово. (Слайд 6) 1)6a3x-9a2y; =3a2(2ax-3y) Е 2) ac+ad+2bc+2bd; =(c+d)(a+2b) В 3) c2-4; =(c-2)(c+2) К 4)x2-2x+1; =(x-1)2 Л 5) 5a2-5ax-7a+7x; =(a-x)(5a-7) И 6)4b2+4b+1. = (2b+1)2 Д | Разбиваемся на группы решают примеры в группах и составят ответ |
-
|
| «Евклид». На стр.206 прочитайте о формулах сокращённого умножения. (Слайд 8) Некоторые правила сокращённого умножения были известны ещё около 4 тыс.лет тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически. У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили, на « a2», а «квадрат на отрезке a», не « ab», а «прямоугольник, содержащийся между отрезками a и b». Например, тождество (a + b)2= a2+ 2аb + b2 во второй книге «Начала» Евклида(3 в.до н.э.) формулировалось так: «Если прямая линия ( имеется в виду отрезок) как- либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключённым между отрезками». Некоторые термины подобного геометрического изложения алгебры сохранились до сих пор. Так, мы называем вторую степень числа квадратом, а третью степень – кубом. Что поняли? Что запомнилось? Евклид был учёным-одиночкой, ему приходилось работать одному. Вам должно быть легче работать в группах. | Читают про формулы сокращенного умножения на с. 206 |
-
|
| Первый пример был с использованием, какого способа? А второй? Третий?
Четвёртый?
Пятый? И шестой?
Где возможно применить? | ( Вынесение общего множителя за скобки)
(Способ группировки). С помощью формул сокращенного умножения.
(С помощью формул сокращенного умножения). (Способ группировки). С помощью формул сокращенного умножения 1.: При решении уравнений х2 – 15х +56 =0; При доказательстве тождеств: (а2 +3а)2 +2(а2 +3а)= а(а+1)(а+2)(а+3); |
-
| Постановка гипотезы | Возвращаемся к нашему заданию. Как настоящие учёные - исследователи, мы должны выдвинуть гипотезу: как выполнить задание?
Я предлагаю разбить наше выражение на мелкие части. Ведь если есть одна большая проблема, решать её сложно, а разбив её на маленькие части, мы сможем постепенно, теми способами, которые мы знаем разрешить её. Но для начала я предлагаю вам выполнить следующее задание. (Слайд10).Выполните разложение многочлена на множители, выбрав любой уровень, эта работа индивидуальная. Задание выполняет каждый, на карточке, их подпишите. | Варианты ответов
Выполнение задания |
-
|
| Давайте сверим ответы. Кто выполнял задания 1 уровня? Кто -2уровня? | Сверяются с доской |
-
| Доказательство гипотезы | Наша гипотеза, что выражение можно, разложить на множители, разбив его на мелкие части, может подтвердиться, а может, и нет. Давайте проверим.
Кто может выйти к доске и собрать все части вместе? X6+2 X5+9 X4+16 X3+24 X2+32 X+16= (X6+2 X5+ X4)+ (8X4+16 X3+8 X2)+ (16 X2+32 X+16)= =X4(X+1)2+8 X2(X+1)2+16(X+1)2=(X+1)2(X4+8 X2+16)= (X+1)2(X2+4). Если X=2, то (2+1)2(22+4)2=32 * 82=9*64=576. Когда легче найти значение многочлена, до его разложения на множители или после? | Выходят к доске
После. |
-
| Вывод | Мы решили одно задание, а, сколько знаний мы при этом использовали! Давайте дозаполним нашу таблицу, которую мы начали в начале урока
Какие способы мы применяли для разложения многочлена на множители?
Мы с вами составили определенный алгоритм для разложения многочлена на множители: (Слайд 18) Вынести общий множитель за скобку (если он есть). Попробовать разложить многочлен на множители по формулам сокращенного умножения. Попытаться применить способ группировки (если предыдущие способы не привели к цели). Для решения любой проблемы нужна большая теоретическая база и навыки практического применения алгоритмов. |
|
-
|
| Давайте ещё раз повторим, какие этапы пути мы прошли с вами как исследователи. | Отвечают |
|
-
| Домашнее задание | Ребята я вам предлагаю необычное домашнее задание: Повторить формулы сокращенного умножения, способы разложения многочлена на множители, |
|
|
-
| Рефлексия | Ребята давайте с вами оценим свою работу: По принципу: 5 – понял материал и объясню другому, 4 – понял материал, но объяснить не смогу 3 – материал не понял | Оценивают свои возможности |
|