план урока для студентов 1 курса.
5. Знакомство с темой урока, совместное целеполагание.
II . Актуализация комплекса знаний и способов действий. Устная фронтальная работа. Метод «Мозговой штурм»
Вопросы:
Что такое функция? Что называют аргументом функции? Как обозначают область определения? Как обозначают множество значений? Как называют переменную х ? Как называют переменную у ? Назовите виды преобразований над графиками функций
Просмотр содержимого документа
«Разработка урока»
КРАТКОСРОЧНЫЙ ПЛАН
Урок №14 Алгебра и начала анализа
5.10.2019г.
10 класс
Тема Свойства функции
Основные цели и задачи урока
Образовательные:
Ввести понятия: «чётная функция», «не чётная функция», «периодическая функция», «ограниченная функция», «промежутки знакопостоянства», «возрастающая функция», «убывающая функция», «окрестность точки», «точка минимума», «точка максимума», «обратная функция».
Формировать умения и навыки функции определять свойства любой функции.
Развивающие:
развивать логическое мышление, навыки анализа и синтеза;
развивать навыки установки причинно-следственных связей между изучаемыми объектами;
развивать устную и письменную культуру речи..
Воспитательные:
содействовать осознанию учащимися ценности изучаемого предмета;
формировать навыки умственного труда – поиск рациональных путей выполнения работы.
Ожидаемые результаты освоения темы
Учащиеся должны знать: свойства функции.
Учащиеся должны уметь: читать графики, по графику определить нужные свойства и значения.
Тип урока
изучение новой темы
Методы обучения
словесные, наглядные, постановки учебной проблемы, практические (самостоятельная работа).
Формы организации учебной деятельности учащихся
фронтальная работа, индивидуальная, работа в группах.
Используемые интерактивные методы обучения
проблемное обучение, обучение в сотрудничестве, личностно-ориентированное обучение, коммуникативные и здоровьесберегающие технологии.
Применение модулей
Обучение тому, как обучаться, Обучение критическому мышлению, Оценивания для обучения, Использование ИКТ в преподавании и обучения, . Обучение талантливых и одарённых детей. Преподавание и обучение в соответствии с возрастными особенностями.
Оборудование и материалы
Учебник, интерактивная доска, проектор, ПК, презентация, памятки
Ход урока
I . Организация начала занятия.
1. Приветствие. Круг добра «Комплимент».
2. Проверка отсутствующих.
3. Деление класса на группы способом «Стикер».
4. Распределить роли.
5. Знакомство с темой урока, совместное целеполагание.
II . Актуализация комплекса знаний и способов действий. Устная фронтальная работа. Метод «Мозговой штурм»
Вопросы:
Что такое функция?
Что называют аргументом функции?
Как обозначают область определения?
Как обозначают множество значений?
Как называют переменную х ?
Как называют переменную у ?
Назовите виды преобразований над графиками функций
Задание. Какие преобразования необходимо выполнить для построения графиков функций?
Функция
Виды преобразований
у=х-1,5
параллельный перенос по оси ОУ на 1,5 вниз
у=2х
растяжение по оси ОХ в 2 раза
у=-3х
растяжение по оси ОХ в -3 раза
у=-2х+3,5
растяжение по оси ОХ в -2 раза и параллельный перенос по оси ОУ на 3,5 вверх
растяжение по оси ОУ в 4 раза и параллельный перенос по оси ОУ на 1 вниз
сжатие по оси ОУ в 2 раза
III . Изучение новой темы.
Рассмотрим свойства функции (Работа по памятке)
«Свойства функции»
Памятка
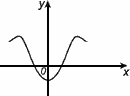
1. Чётность и нечётность
Функция четная,
f(-x) = f(x)
Св-во: 0y
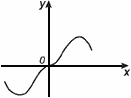
Функция нечетная, f(-x) = –f(x)
Св-во:
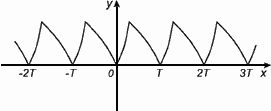
2.Периодичность
Функция f(x) периодическая, если f(x) = f(x+Т) = f(x-Т),
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
3. Монотонность (возрастание, убывание)
Функция f(x) возрастает , если x1 2 и f(x 1 )2 ).
Функция f(x) убывает , если x1 2 и f(x 1 ) f(x 2 ).
Функция f(x) не возрастает ,
если x1 2 и f(x 1 ) ≥ f(x 2 ).
Функция f(x) не убывает ,
если x1 2 и f(x 1 ) ≤ f(x 2 ).
4. Промежутки знакопостоянства
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
Промежуток, на котором y0, график находится выше оси ОХ.
Промежуток, на котором yY
5.Ограниченность и неограниченность.
Функция называется ограниченной, если, |f(x)| ≤ b , b0
Если b0 не существует, то функция - неограниченная.
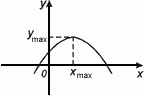
6. Экстремумы
Xmin , Хmax – точки экстремумаmin , Уmax – экстремумы.
Х max точка максимума , если f(х) f(X max ).
Y max =f(X max ) - максимум функции.
Х min точка минимума , если f(х) f(X min ).
Y min =f(X min ) - минимум функции.
Рассмотрим примеры:
Пример 1. Исследовать на четность и нечетность функцию:
б) в)
Решение:
а)
функция f(x) – чётная
б)
функция f(x) – не чётная
в)
функция не является ни чётной, ни нечётной.
Пример 2. Найти период функции y=cos(3x+2)
функция
период
y=cos (x)
T=2π
y=cos(3x+2), a=3
Пример 3. Определить промежутки знакопостоянства функции y=4x-2
Решение:
y=4x-2 =2(2x-1)
2(2x-1)=0
2x-1=0
2x=1
x=1/2
y0 (1/2; + ∞ )
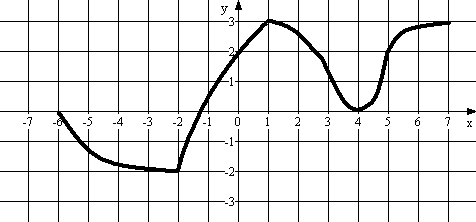
Пример 4. По графику определите промежутки монотонности функции
Решение:
Функция убывает на промежутках:
(-6;-2) и (1;4)
Функция возрастает на промежутках:
(-2;-1) и (4;+∞)
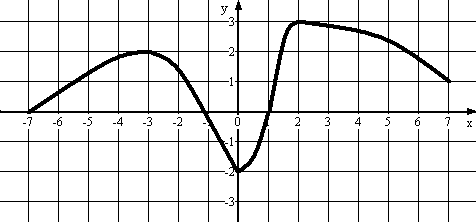
Пример 5. По графику определите экстремумы функции
Решение:
Y max =3, X max = 1,8
Y min = -2, X min = 0
IV . Закрепление нового материала
Работа по группам
Задания из учебника
(ЕМН) (ОГН)
1 группа № 29, 25
2 группа №30, 26
3 группа №31, 27
4 группа №36 30
Защита работ по методу «Вертушка»
V . Подведение итогов урока.
1. Как найти точки пересечения графика функции с осями координат?
2. Какая функция является возрастающей?
3. Какая функция является убывающей?
4. Что значит экстремумы функции?
5. Как определить чётность или нечётность функции?
VI . Рефлексия. Метод «3 минутное эссе»
На цветных стикерах написать своё отношение к уроку
VII . Домашнее задание.
стр. 25 №35, 37, выучить памятку (ЕМН)