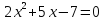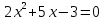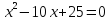Конспект урока по смысловому чтению

Данный конспект поможет провести урок не только качественно с объяснением нового материала, но и использовать технологии сингапурских практик, а также приемы смыслового чтения.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Конспект урока по смысловому чтению»

Технологическая карта урока

Педагогическое обоснование урока

Тема	Формулы корней квадратного уравнения, 8 класс
Цель темы	обобщить знания учащихся, полученные при изучении темы «Методы решения квадратных уравнений», а также изучить и первично закрепить алгоритм решения полного квадратного уравнения.
Планируемый результат	Предметные. Учащиеся научатся: - При чтении текстов, предложенных на уроке, осуществлять поиск информации и понимать прочитанное. - моделировать ситуацию, иллюстрирующую алгоритм решения квадратного уравнения по формулам корней квадратного уравнения. Учащиеся получат возможность - выбрать алгоритм решения нестандартной задачи. Метапредметные. Регулятивные: – определить цель и проблему в учебном процессе, - действовать по алгоритму - уметь работать со схемой - рефлексия. Познавательные: – понимать информацию и извлекать информацию из текста Коммуникативные: – осознанная речь (слушать, говорить, осознанно читать вслух) - участие в беседе. Личностные. Ученик разовьет: - внимательность; - аккуратность в вычислениях; - память; - требовательное отношение к себе и своей работе. Ученик получит возможность: - развития познавательного интереса к изучению предмета, самовоспитания; - давать позитивную самооценку результата учебной деятельности.
Основные понятия	Квадратное уравнение, дискриминант, корни уравнения, алгоритм решения квадратных уравнений.
Межпредметные связи	История, русский язык
Ресурсы: - основные - дополнительные	Ноутбук, проектор, презентация по теме урока «формулы корней квадратного уравнения»
Организация пространства (работа фронтальная, индивидуальная, в парах)	Работа фронтальная, индивидуальная

Курсивом в технологической карте выделено смысловое чтение текста учащимися

Содержание урока и деятельности участников образовательного процесса.

Этап урока

Деятельность учителя

Деятельность ученика

УУД

1.Организационный момент

Приветствие и проверка подготовленности обучающихся к уроку.

Включаются в деловой ритм урока.

Коммуникативные УУД: планирование учебного сотрудничества с учителем и одноклассниками.

2. Актуализация знаний. Мотивация обучающихся.

«Неизвестное X, неизвестное Y,

Их можно в равенствах повстречать.

И это, ребята, скажу вам, не игры,

Здесь нужно решение всерьез отыскать.

С неизвестными равенства, без сомнения,

Называем, ребята, мы как? »

- О чем эта загадка?

Подскажите, какую тему мы изучаем? Рассказывает о приеме «Ромашка Блума»

Ромашка Блума (отрываем 7 лепестков в порядке цветов радуги):

Красный – Сформулируйте определение квадратного уравнения.

Оранжевый – Объясните, в чём заключается смысл ограничения в определении квадратного уравнения

Жёлтый – Придумайте неполные квадратные уравнения.

Зелёный – Составьте квадратное уравнение, в котором главный коэффициент равен 5, свободный член равен -15, второй коэффициент равен -25.

ПАУЗА. Давайте совершим краткий экскурс в историю квадратных уравнений.

Историческая справка. Учитель выдает детям напечатанный текст (цель: проверка понимания читаемого текста):

«Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет».

Лейбниц

Неполные квадратные уравнения умели решать вавилоняне (около 2 тыс. лет до н.э.). Об этом свидетельствуют найденные клинописные тексты задач с решениями (в виде рецептов).

Некоторые виды квадратных уравнений могли решать древнегреческие математики, сводя их решения к геометрическим построениям.

Приёмы решения уравнений без обращения к геометрии даёт Диофант Александрийский (III в).

Правило решения квадратных уравнений, приведённых к виду,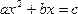

где не равно нулю, дал индийский математик и астроном Брахмагупта (VII в.).

В IX веке узбекский математик Аль-Хорезми в трактате “Алгебра” классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь. В своих трудах хорезмский математик отыскивает только положительные корни, т.к. отрицательных чисел тогда не признавали.

После трудов нидерландского математика А.Жирара (1595-1632), а также Ньютона (1642-1727) и Декарта (1596-1650) способ решения квадратных уравнений принял современный вид.

В XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым он заложил основы буквенной алгебры. Виет доказал формулы, выражающие зависимость корней уравнения от его коэффициентов.

Предлагает ответить учащимся на вопросы.

Вопросы для учащихся:

Какой вклад в решение квадратных уравнений внес Брахмагупта? (находить в тексте конкретные сведения).
Когда зародилась Киевская Русь? (находить в тексте конкретные сведения)
Расположите великих математиков в хронологическом порядке. (понимать информацию, представленную разным способом – года, век)
Назовите имя математика, который ввёл буквы в алгебру.(находить в тексте конкретный факт.

Предлагает продолжить работу с «Ромашкой Блума».

Голубой - Поделитесь, какие способы решения полных квадратных уравнений вы знаете.

Синий – Почему изученные методы нельзя отнести к универсальным.

Фиолетовый – Предположите, чем мы будем заниматься на уроке (используйте ключевые слова – универсальный, рациональный, специальный, общий, удобный). Метод предвосхищения

Уравнение

Квадратные уравнения.

Внимательно слушают, отвечают на вопросы, выполняют задания.

Читают внимательно текст.

Отвечают на вопросы.

Познавательные УУД (поиск и выделение необходимой информации, осознанное высказывание, формирование мыслительных операций)

Коммуникативные УУД (умение с достаточной полнотой и точностью выражать свои мысли).

Регулятивные УУД (целеполагание).

Личностные УУД (самоопределение,смыслообразование).

3. Формулирование темы урока.

Постановка целей урока.

Давайте совместными усилиями сформулируем тему урока.

Почему нам необходим новый способ решения уравнений?

Формулируют тему урока и записывают в тетрадь, определяют цель.

«Новый способ решения квадратных уравнений».

Научиться решать уравнения новым способом. Не все уравнения решаемы способами, которые уже известны.

Регулятивные: целеполагание

Коммуникативные: постановка вопросов.

Познавательные: самостоятельное формулирование проблемы

4. «Открытие» учащимися новых знаний

Выдает учащимся раздаточный материал, проверяет понимание информации, представленной словесно.

Квадратным уравнением называется уравнение вида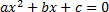, где

х – переменная; a,b,c - постоянные (числовые) коэффициенты.

Формула дискриминанта: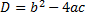

В общем случае решение квадратных уравнений сводится к нахождению дискриминанта. Дискриминант – это выражение равное 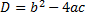, дискриминант обозначается буквой D. Термин «дискриминант» ввёл английский математик Сильвестр Джеймс Джозеф.

Два слова (дискриминант и дискриминация) происходят от одного латинского слова, означающего “различающий”. Дискриминация – это унижение одних и возвышение других, т.е. различное отношение к разным людям. Дискриминант различает квадратные уравнения по числу корней.

О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

D0 - уравнение имеет 2 различных действительных корня
D=0 - уравнение имеет 2 совпадающих действительных корня (в этом случае принято говорить, что квадратное уравнение имеет один корень, так как значения корней равны).
D

В общем случае корни уравнения равны: .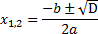

Очевидно, в случае с нулевым дискриминантом, оба корня равны .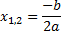

Проверяет умение находить конкретную информацию.

Кто ввёл термин «дискриминант»?

Что означает слово «дискриминант»?

Главный вопрос – познакомились ли вы с правилом решения квадратных уравнений? (умение понимать алгоритм, записанный словесно). Давайте посмотрим на слайд в презентации, где правило решения квадратных уравнений предложено в виде схемы (умение работать со схемой).

Просит помощи у ребят восстановить данный алгоритм на доске (Используя приём «деформированный текст» , предлагает учащимся восстановить алгоритм решения полного квадратного уравнения по формуле, который в перепутанном виде представлен на доске).

Выдает памятку учащимся.

«Скажи мне – и я забуду, покажи мне – и я запомню, дай мне сделать – и я пойму»

Конфуции

Знакомство с новым способом решения квадратных уравнений.

После прочтения, учащиеся отвечают на вопросы

Вставляют пропуски в алгоритм. Еще раз просматривают памятку.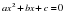

Правило решения полного квадратного уравнения

Определить коэффициенты a,b,c.
Вычислить дискриминант по формуле___________
Если D __________, то квадратное уравнение не имеет действительных корней.
Если D = 0, то квадратное уравнение имеет один корень . Он находится по формуле_____________

Если D ______0, то квадратное уравнение имеет два корня: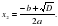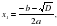

Коммуникативные: инициативное сотрудничество, выражение своих мыслей с достаточной полнотой и точностью; аргументация своего мнения и позиции в коммуникации

Регулятивные: планирование

Познавательные: Самостоятельное формулирование цели.

Решение проблемы, построение логической цепи рассуждений, доказательство, выдвижение гипотез и их обоснование

Первичное закрепление знаний

Решает совместно с учащимися квадратное уравнение.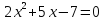

Предлагает квадратные уравнения для самостоятельного решения. Используется метод Clock Buddies. затем показывает их решения на обратной стороне доски.

Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок, акцентирует внимание учащихся на значимости темы.

Совместно с учителем решают квадратное уравнение, один у доски, остальные в тетради. Записывают решение в тетрадь.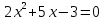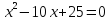

Ученики в тетрадях выполняют решение уравнений.

Используется метод Clock Buddies. Ребята рисуют в тетради циферблат часов. Назначают встречу 2 одноклассникам, осуществляют взаимопроверку, затем проверяют решение по записям на обратной стороне доски.

Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения квадратных уравнений.

Регулятивные: контроль, оценка, коррекция.

Познавательные: умение структурировать знания, выбор наиболее эффективных способов решения задач.

Рефлексия. Сообщение домашнего задания.

Подводит итоги урока.

Почему необходим новый способ решения? Как его можно назвать? Закончить сегодняшний урок хотелось бы словами английского математика и педагога Уолтера Варвика Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи.

Дает комментарий к домашнему заданию.

Домашнее задание:

Выучить алгоритм решения квадратных уравнений.
Решите уравнение (х²-х)²- 14(х²-х) + 24 = 0 методом введения новой переменной.
Решите уравнение 3х²+ 5х + 2 = 0:
1. используя формулу дискриминанта – «3»,
2. двумя способами – «4»,
3. тремя способами – «5».