оперировать понятиями: конечное множество, элемент множества, подмножество, пересечение и объединение множеств, числовые множества на координатной прямой, отрезок, интервал, полуинтервал, промежуток с выколотой точкой, графическое представление множеств на координатной плоскости;
оперировать понятиями: утверждение, отрицание утверждения, истинные и ложные утверждения, причина, следствие, частный случай общего утверждения, контрпример;
проверять принадлежность элемента множеству;
находить пересечение и объединение множеств, в том числе представленных графически на числовой прямой и на координатной плоскости;
строить на числовой прямой подмножество числового множества, заданное простейшими условиями;
распознавать ложные утверждения, ошибки в рассуждениях, в том числе с использованием контрпримеров;
проводить доказательные рассуждения для обоснования истинности утверждений;
выполнять арифметические действия с целыми и рациональными числами;
выполнять несложные преобразования числовых выражений, содержащих степени чисел, либо корни из чисел, либо логарифмы чисел;
сравнивать рациональные числа между собой;
оценивать и сравнивать с рациональными числами значения целых степеней чисел, корней натуральной степени из чисел, логарифмов чисел в простых случаях;
изображать точками на числовой прямой целые и рациональные числа;
изображать точками на числовой прямой целые степени чисел, корни натуральной степени из чисел, логарифмы чисел в простых случаях;
выполнять несложные преобразования целых и дробно-рациональных буквенных выражений;
выражать в простейших случаях из равенства одну переменную через другие;
вычислять в простых случаях значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
выполнять арифметические действия, сочетая устные и письменные приемы, применяя при необходимости вычислительные устройства;
пользоваться оценкой и прикидкой при практических расчетах;
использовать методы решения уравнений: приведение к виду «произведение равно нулю» или «частное равно нулю», замена переменных;
использовать графический метод для приближенного решения уравнений и неравенств;
оперировать понятиями: зависимость величин, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание на числовом промежутке, убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, периодическая функция, период, четная и нечетная функции;
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
строить эскиз графика функции, удовлетворяющей приведенному набору условий (промежутки возрастания/убывания, значение функции в заданной точке, точки экстремумов, асимптоты, нули функции и т.д.);
оперировать на базовом уровне понятиями: тригонометрические функции;
распознавать графики элементарных тригонометрических функций;
соотносить графики элементарных тригонометрических функций с формулами, которыми они заданы;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
оперировать на базовом уровне понятиями: производная функции в точке, касательная к графику функции, производная функции;
определять значение производной функции в точке по изображению касательной к графику, проведенной в этой точке;
решать несложные задачи на применение связи между промежутками монотонности и точками экстремума функции, с одной стороны, и промежутками знакопостоянства и нулями производной этой функции – с другой.
Решать несложные текстовые задачи разных типов;
анализировать условие задачи, при необходимости строить для ее решения математическую модель;
понимать и использовать для решения задачи информацию, представленную в виде текстовой и символьной записи, схем, таблиц, диаграмм, графиков, рисунков;
действовать по алгоритму, содержащемуся в условии задачи;
использовать логические рассуждения при решении задачи;
работать с избыточными условиями, выбирая из всей информации, данные, необходимые для решения задачи;
осуществлять несложный перебор возможных решений, выбирая из них оптимальное по критериям, сформулированным в условии;
анализировать и интерпретировать полученные решения в контексте условия задачи, выбирать решения, не противоречащие контексту;
решать задачи на расчет стоимости покупок, услуг, поездок и т.п.;
решать несложные задачи, связанные с долевым участием во владении фирмой, предприятием, недвижимостью;
решать задачи на простые проценты (системы скидок, комиссии) и на вычисление сложных процентов в различных схемах вкладов, кредитов и ипотек;
решать практические задачи, требующие использования отрицательных чисел: на определение температуры, на определение положения на временнóй оси (до нашей эры и после), на движение денежных средств (приход/расход), на определение глубины/высоты и т.п.;
Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Периодические функции. Четность и нечетность функций. Тригонометрические функции 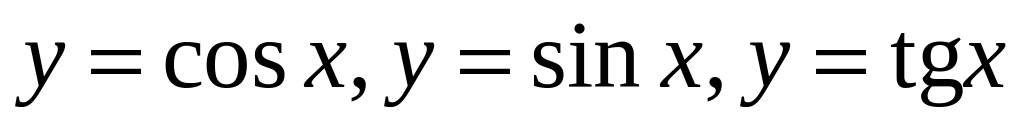 . Функция
. Функция 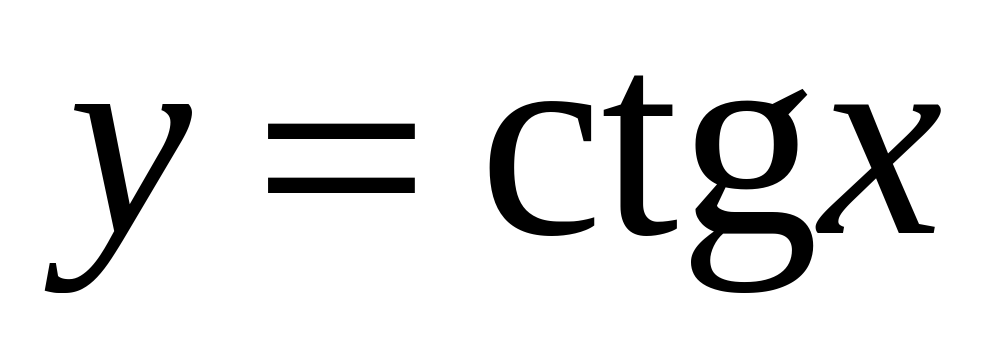 . Свойства и графики тригонометрических функций.
. Свойства и графики тригонометрических функций.
Степень с действительным показателем, свойства степени. Простейшие показательные уравнения и неравенства. Показательная функция и ее свойства и график.
Логарифм числа, свойства логарифма. Десятичный логарифм. Число е. Натуральный логарифм. Преобразование логарифмических выражений. Логарифмические уравнения и неравенства. Логарифмическая функция и ее свойства и график.
Степенная функция и ее свойства и график. Иррациональные уравнения.
Производная функции в точке. Касательная к графику функции. Геометрический и физический смысл производной. Производные элементарных функций. Правила дифференцирования.
Вторая производная, ее геометрический и физический смысл.
Понятие о непрерывных функциях. Точки экстремума (максимума и минимума). Исследование элементарных функций на точки экстремума, наибольшее и наименьшее значение с помощью производной. Построение графиков функций с помощью производных. Применение производной при решении задач.
Первообразная. Первообразные элементарных функций. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Определенный интеграл. Вычисление площадей плоских фигур и объемов тел вращения с помощью интеграла.
| № п/п | Тема урока | Количество часов | Дата |
| План | Корректировка |
| 1. | Повторение ( 6 часа) |
| 1.1. | Повторение | 4 |
|
|
| 1.2. | Входящая контрольная работа | 2 |
|
|
| 2. | Тригонометрические функции ( 16 часов) |
| 2.1. | Область определения и множество значений тригонометрических функций. | 3 |
|
|
| 2.2. | Чётность, нечётность, периодичность тригонометрических функций. | 3 |
|
|
| 2.3. | Свойство функции y=cos x и её график | 3 |
|
|
| 2.4. | Свойство функции y=sin x и её график | 2 |
|
|
| 2.5. | Свойство функции y=tg x и её график | 2 |
|
|
| 2.6. | Обратные тригонометрические функции | 1 |
|
|
| 2.7. | Урок обобщения, систематизации и коррекции | 1 |
|
|
| 2.8. | Проверочная работа « Тригонометрические функции» | 1 |
|
|
| 3. | Производная и её геометрический смысл (16 часов) |
| 3.1. | Производная | 2 |
|
|
| 3.2. | Производная степенной функции | 2 |
|
|
| 3.3. | Правила дифференцирования | 3 |
|
|
| 3.4. | Производная некоторых элементарных функций | 3 |
|
|
| 3.5. | Самостоятельная работа | 1 |
|
|
| 3.6. | Геометрический смысл производной | 3 |
|
|
| 3.7. | Урок обобщения , коррекции и развития | 1 |
|
|
| 3.8. | Проверочная работа «Производная и её геометрический смысл» | 1 |
|
|
| 4. | Применение производной к исследованию функции (18 часов)) |
| 4.1. | Возрастание и убывание функции | 3 |
|
|
| 4.2. | Промежуточная контрольная работа | 1 |
|
|
| 4.3. | Экстремумы функции | 3 |
|
|
| 4.4. | Применение производной к построению графиков функций | 2 |
|
|
| 4.5. | Самостоятельная работа | 1 |
|
|
| 4.6. | Наименьшее и наибольшее значение функции | 4 |
|
|
| 4.7. | Выпуклость графика функции, точки перегиба | 1 |
|
|
| 4.8. | Решение задач | 1 |
|
|
| 4.9. | Урок обобщения , коррекции и развития | 1 |
|
|
| 4.10. | Проверочная работа «Применение производной к исследованию функции» | 1 |
|
|
| 5. | Интеграл ( 19 часов) |
| 5.1. | Первообразная | 2 |
|
|
| 5.2. | Правила нахождения первообразных | 2 |
|
|
| 5.3. | Площадь криволинейной трапеции и интеграл | 3 |
|
|
| 5.4. | Вычисление интегралов | 2 |
|
|
| 5.5. | Вычисление площадей с помощью интегралов | 4 |
|
|
| 5.6. | Применение производной и интеграла к решению практических задач | 3 |
|
|
| 5.7. | Решение задач | 1 |
|
|
| 5.8. | Урок обобщения , коррекции и развития | 1 |
|
|
| 5.9. | Проверочная работа « Интеграл» | 1 |
|
|
| 6. | Итоговое повторение курса алгебры и начал математического анализа ( 27 часов) |
| 6.1. | Выражения и преобразования | 7 |
|
|
| 6.2. | Уравнения и неравенства | 4 |
|
|
| 6.3. | Функции | 4 |
|
|
| 6.4. | Текстовые задачи | 5 |
|
|
| 6.6. | Решение вариантов ЕГЭ* | 7 |
|
|
| *данные часы могут быть перераспределены на диагностические и тренировочные работы в течение всего учебного года. |
















