Содержание.
Пояснительная записка.
Содержание тем учебного курса.
Учебно-тематический план.
Требования к уровню подготовки выпускников.
Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре и началам анализа
Литература для учащихся и учителя.
Приложение:
-календарно-тематическое планирование;
-контрольно-измерительные материалы.
Пояснительная записка
Статус документа
Данная рабочая программа ориентирована на учащихся 11 класса социально-экономического и агротехнологического профилей и реализуется на основе следующих нормативных документов:
Закон «Об образовании » Российской Федерации
Федеральный компонент государственного стандарта общего образования. Математика
Примерная программа среднего (полного) общего образования по математике. Профильный уровень.
Программы по алгебре и началам математического анализа. 11 класс /Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров, М.В Ткачева и др./Сборник. Программы общеобразовательных учреждений. Алгебра и начала анализа. 10-11 класс. Составитель Бурмистрова Т. А.– М: «Просвещение», 2009
Программа по геометрии (базовый и профильный уровни). 11 класс / Атанасян Л.С, Бутузов В.Ф., Кадомцев С.Б. и др. Сборник. Программы общеобразовательных учреждений. Геометрия. 10-11 класс. Составитель Бурмистрова Т. А.– М: «Просвещение», 2010
Образовательная программа и базисный учебный план МОУ Новомалыклинской СОШ на 2014 – 2015 учебный год.
Федеральный перечень учебников, рекомендованных Министерством образования и науки Российской Федерации к использованию в образовательном процессе в имеющих государственную аккредитацию и реализующих образовательные программы общего образования образовательных учреждениях, на 2014/2015 учебный год
Общая характеристика учебного предмета
В профильном курсе содержание образования, представленное в основной школе, развивается в следующих направлениях:
• систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объёме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
расширение системы сведений о свойствах плоских фигур, систематическое изучении свойств пространственных тел, развитие представлений о геометрических измерениях;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Цели
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
• формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
• овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, дли продолжения образования и освоения избранной специальности на современном уровне;
• развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творчески: способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и её приложений в будущей профессиональной деятельности;
• воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
Задачи, решаемые при реализации рабочей программы:
- систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе и его применение к решению математических и нематематических задач;
- расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
- изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач;
- развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
- знакомство с основными идеями и методами математического анализа.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе среднего (полного) общего образования в социально-экономическом профиле отводится 6 часов в неделю при 34 недельной работе; в агротехнологическом профиле отводится 5 часов в неделю при 34 недельной работе и один час в неделю добавляется из школьного компонента.
Рабочая программа ориентирована на использование учебно-методических комплексов:
Алгебра и начала математического анализа. Учебник для 10-11 классов общеобразовательных учреждений. / Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др./ М.: Просвещение, 2010.
Изучение алгебры и начал математического анализа в 10-11 кл. Книга для учителя. /Федорова Н. Е./ М.: Просвещение, 2011
Алгебра и начала математического анализа. Тематические тесты. 10-11 классы. / Ткачева М./ М.: Просвещение, 2012.
Геометрия, 10-11. Учебник для общеобразовательных учреждений: базовый и профильный уровни/ Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.–18-е издание./ М.: Просвещение, 2009
Дидактические материалы по геометрии для 10-11 кл. /Зив Б.Г., Мейлер В.М./ М.: Просвещение, 2001
Задачи по геометрии для 7 – 11 классов. /Б. Г. Зив, В. М. Мейлер, А. П. Баханский./ М.: Просвещение, 2003.
Рабочая тетрадь по геометрии для 10 -11 классов. /Ю. А. Глазков, И. И. Юдина, В. Ф. Бутузов./ М.: Просвещение, 2011.
Изучение геометрии в 10—11 классах: книга для учителя. /Саакян С. М. , Бутузов В. Ф./ М.: Просвещение, 2003.
Формы организации учебного процесса: индивидуальные, групповые, индивидуально-групповые, фронтальные, классные и внеклассные.
Формы контроля: самостоятельная работа, контрольная работа, тест, работа по карточкам.
Технические средства обучения: компьютер, медиапроектор, интерактивная доска.
Содержание тем учебного курса
Тема 1. «Повторение курса алгебры и начал анализа 10 класса»
Основная цель: Повторить курс алгебры и начал математического анализа за 10 класс.
Раздел математики. Сквозная линия
Числа и вычисления
Функции
Обязательный минимум содержания образовательной области математика
Действительные числа.
Степенная функция, ее свойства и график.
Показательная функция, ее свойства и график.
Логарифмическая функция, ее свойства и график.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь решать несложные алгебраические, иррациональные, показательные, логарифмические, тригонометрические уравнения, неравенства и их системы.
Знать свойства степенной, показательной, логарифмической функций и уметь строить их графики.
Уровень возможной подготовки обучающегося
Уметь решать алгебраические, иррациональные, показательные, логарифмические, тригонометрические уравнения, неравенства и их системы, применяя различные методы их решений.
Знать свойства степенной, показательной, логарифмической функций и уметь строить их графики. Уметь применять свойства функций при решении различных задач.
Тема 2. «Тригонометрические функции»
Основная цель: изучить свойства тригонометрических функций, научить учащихся применять эти свойства при решении уравнений и неравенств, научить строить графики тригонометрических функций.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Область определения тригонометрических функций.
Множество значений тригонометрических функций.
Четность, нечетность, периодичность тригонометрических функций.
Свойства функций у=cosx, y=sinx.
Графики функций у=cos x, y=sinx.
Свойства функции y=tgx
График функции y=tgx.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Научиться находить область определения тригонометрических функций.
Научиться находить множество значений тригонометрических функций.
Научиться определять четность, нечетность, периодичность тригонометрических функций.
Знать свойства тригонометрических функций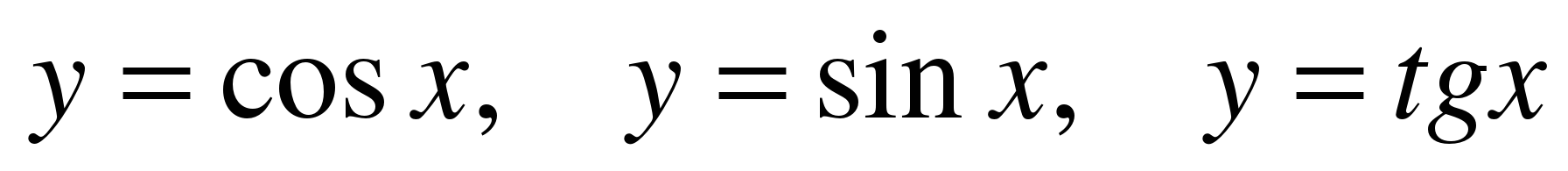 
и уметь строить их графики.
Уровень возможной подготовки обучающегося
Научиться находить область определения и множество значений тригонометрических функций в более сложных случаях.
Научиться определять четность, нечетность, периодичность тригонометрических функций в более сложных случаях.
Знать свойства тригонометрических функций 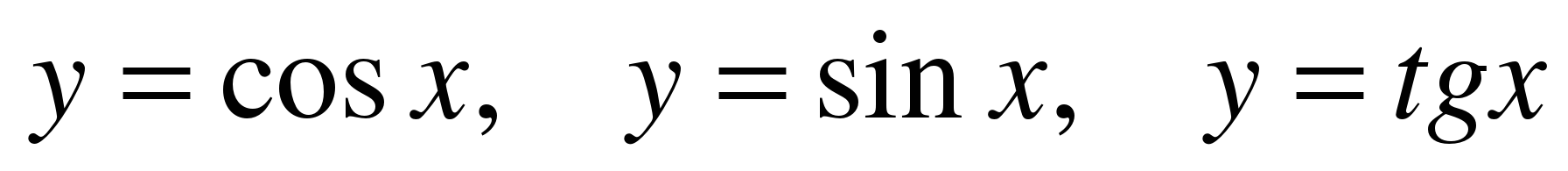и уметь строить их графики. Уметь выполнять преобразования графиков.
описывать по графику и в простейших случаях по формуле поведение и свойства тригонометрических функций, находить по графику функции наибольшие и наименьшие значения;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Тема 3. «Метод координат в пространстве».
Основная цель – сформировать умения учащихся применять векторно-координатный метод к решению задач на вычисление углов между прямыми и плоскостями и расстояний между двумя точками, от точки до плоскости.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Прямоугольная система координат в пространстве.
Координаты вектора.
Связь между координатами вектора и координатами точек.
Простейшие задачи в координатах.
Угол между векторами.
Вычисление углов между прямыми и плоскостями.
Движения
Требования к математической подготовке
Обязательный минимум содержания образовательной области математика
Знать и уметь применять формулы координат середины отрезка, длины вектора через его координаты, расстояние между двумя точками, формулу скалярного произведения;
Уметь строить точки в прямоугольной системе координат по заданным её координатам и находить координаты точки в заданной системе координат;
Решать простейшие задачи в координатах;
Находить угол между векторами по их координатам.
Уровень возможной подготовки обучающегося
Вычислять углы между прямыми и плоскостям;
Строить симметричные фигуры;
Применять координатно-векторный метод для вычисления отношений, расстояний, углов.
Тема 4. «Производная и ее геометрический смысл»
Основная цель: Ввести понятие производной; научить находить производные с помощью формул дифференцирования; научит находить уравнение касательной к графику функции.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Понятие о пределе и непрерывности функции.
Производная. Физический смысл производной.
Таблица производных
Производная суммы, произведения и частного двух функций.
Геометрический смысл производной.
Уравнение касательной.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Понимать механический смысл производной.
Находить производные элементарных функций, пользуясь таблицей производных.
Находить производные элементарных функций, пользуясь правилами дифференцирования.
Понимать геометрический смысл производной.
Уровень возможной подготовки обучающегося
Овладеть понятием производной (возможно на наглядно-интуитивном уровне).
Усвоить механический смысл производной
Освоить технику дифференцирования.
Усвоить геометрический смысл производной.
Тема 5. «Применение производной к исследованию функций»
Основная цель: Показать возможности производной в исследовании свойств функций и построении их графиков.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Исследование свойств функции с помощью производной.
Нахождение промежутков монотонности.
Нахождение экстремумов функции
Построение графиков функций.
Нахождение наибольших и наименьших значений.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Применять производные для исследования функций на монотонность в несложных случаях.
Применять производные для исследования функций на экстремумы в несложных случаях.
Применять производные для исследования функций и построения их графиков в несложных случаях.
Применять производные для нахождения наибольших и наименьших значений функции
Уровень возможной подготовки обучающегося
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Тема 6. «Цилиндр, конус и шар».
Основная цель – дать учащимся систематические сведения об основных телах и поверхностях вращения – цилиндре, конусе, сфере, шаре.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Понятие цилиндра. Площадь поверхности цилиндра.
Понятие конуса. Площадь поверхности конуса. Усечённый конус.
Сфера и шар. Уравнение сферы.
Взаимное расположение сферы и плоскости.
Касательная плоскость к сфере.
Площадь сферы.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Знать и уметь применять формулы для вычисления площадей боковой и полной поверхностей цилиндра; для вычисления площадей боковой и полной поверхностей конуса и усечённого конуса;
Решать задачи на вычисление площади сферы.
Уровень возможной подготовки обучающегося
Тема 7. «Интеграл»
Основная цель: Ознакомить с понятием интеграла и интегрированием как операцией, обратной дифференцированию.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Научиться находить первообразные, пользуясь таблицей первообразных.
Научиться вычислять интегралы в простых случаях.
Научиться находить площадь криволинейной трапеции.
Уровень возможной подготовки обучающегося
Освоить технику нахождения первообразных.
Усвоить геометрический смысл интеграла.
Освоить технику вычисления интегралов.
Научиться находить площади фигур в более сложных случаях.
Тема 8. «Объёмы тел».
Основная цель – ввести понятие объема тела и вывести формулы для вычисления объемов основных многогранников и круглых тел, изученных в курсе стереометрии.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь находить объём прямоугольного параллелепипеда, призмы, пирамиды;
Уметь находить объём цилиндра, конуса, шара;
Уровень возможной подготовки обучающегося
Уметь решать задачи на вычисление объёма призмы, пирамиды, цилиндра, конуса и шара;
Знать способ вычисления объёмов тел с помощью определённого интеграла;
Применять формулы для нахождения объёма наклонной призмы; усечённой пирамиды; усечённого конуса; шарового слоя, шарового сегмента, шарового сектора при решении задач;
Применять формулу площади сферы при решении задач.
Тема 9. «Элементы математической статистики, комбинаторики и теории вероятностей»
Основная цель: развить комбинаторное мышление учащихся; ознакомить с теорией соединений (как самостоятельным разделом математики и в дальнейшем – с аппаратом решения ряда вероятностных задач); обосновать формулу бинома Ньютона сформировать понятие вероятности случайного независимого события; научить решать задачи на применение теоремы о вероятности суммы двух несовместных событий и на нахождение вероятности произведения двух независимых событий, математической статистики.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уровень возможной подготовки обучающегося
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Тема 10 «Комплексные числа»
Основная цель — завершение формирования представления о числе; обучение действиям с комплексными числами и демонстрация решений различных уравнений на множестве комплексных чисел. Рассматриваются четыре арифметических действия с комплексными числами, заданными в алгебраической форме. Вводится понятие комплексной плоскости, на которой иллюстрируется геометрический смысл модуля комплексного числа и модуля разности комплексных чисел. Рассматривается переход от алгебраической к тригонометрической форме записи комплексного числа и обратный переход.
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Комплексные числа.
Сумма, разность, произведение и частное комплексных чисел.
Тригонометрическая форма записи комплексного числа.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь представлять комплексное число в алгебраической и тригонометрической форме.
Уметь изображать число на комплексной плоскости.
Уметь выполнять операции сложения, вычитания, умножения и деления чисел, записанных в алгебраической форме.
Уровень возможной подготовки обучающегося
Тема 11. «Итоговое повторение курса математики»
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Корень степени n.
Степень с рациональным показателем.
Логарифм.
Синус, косинус, тангенс, котангенс. Прогрессии.
Общие приемы решения уравнений. Решение уравнений. Системы уравнений с двумя переменными. Неравенства с одной переменной.
Область определения функции.
Область значений функции.
Периодичность. Четность (нечетность). Возрастание (убывание).
Экстремумы. Наибольшее (наименьшее) значение.
Графики функций.
Производная.
Исследование функции с помощью производной.
Первообразная. Интеграл.
Площадь криволинейной трапеции.
Случайные события и их вероятности.
Параллельность прямых и плоскостей.
Перпендикулярность прямых и плоскостей.
Многогранники.
Метод координат в пространстве.
Цилиндр, конус и шар.
Объёмы тел.
Уровень обязательной подготовки обучающегося
Уметь:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы.
Уровень возможной подготовки обучающегося
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
вычислять площади с использованием первообразной;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем.
строить графики изученных функций;
описывать по графику и по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
построения и исследования простейших математических моделей.
Учебно-тематический план
| № | Тема | Количество часов | Количество контрольных работ |
| 1 | Повторение курса математики 10 класса | 9 | 1 |
| 2 | Тригонометрические функции | 19 | 1 |
| 3 | Метод координат в пространстве | 19 | 2 |
| 4 | Производная и её геометрический смысл | 19 | 1 |
| 5 | Применение производной к исследованию функций | 21 | 1 |
| 6 | Цилиндр, конус, шар | 16 | 1 |
| 7 | Интеграл | 16 | 1 |
| 8 | Объемы тел | 16 | 1 |
| 9 | Комбинаторика | 7 |
|
| 10 | Элементы теории вероятностей | 6 | 1 |
| 11 | Статистика | 5 |
|
| 12 | Комплексные числа | 9 | 1 |
| 13 | Итоговое повторение курса математики | 42 | 1 |
| Всего | 204 | 12 |
Требования к уровню подготовки выпускников
В результате изучения математики на профильном уровне в старшей школе ученик должен
знать / понимать
• значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрического языка как средства описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на
аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира.
уметь:
выполнять арифметические действия, сочетая устные и письменные приёмы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчётах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
определять значение функция по значению аргумента при различных способах задания
функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их
графические представления;
решать рациональные, показательные и логарифмические уравнения и неравенства,
иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений и неравенств, интерпретируя результат с учётом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем;
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять, в простейших случаях, вероятности событий на основе подсчёта числа исходов.
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства;
описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов;
решения геометрических, физических, экономических и других прикладных задач, в том числе
задач на наибольшие и наименьшие значения с применением аппарата математического анализа;
построения и исследования простейших математических моделей;
анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре и началам анализа
1. Оценка письменных контрольных работ.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Общая классификация ошибок
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Литература для учителя.
Алгебра и начала математического анализа, 10 11 классы. Учебник для общеобразовательных учреждений /Ш.А. Алимов [и др.], - М.: Просвещение, 2011г.
Контрольно-измерительные материалы. Алгебра и начала анализа: 11 класс / сост. А.Н. Рурукин. – М.: ВАКО, 2011
3. Дидактические материалы по алгебре и началам анализа. 10-11 классы. / П.И. Алтынов. / М: Дрофа, 1999
4. Задачи по алгебре и началам математического анализа. 10-11 классы: пособие для учащихся общеобразовательных учреждений / С.М.Саакян, А.М.Гольдман, Д.В.Денисов/ М.: Просвещение, 2009.
5. Сборник задач по алгебре и началам математического анализа: учебное пособие для 10-11 классов с углубленным изучением математики / А.П.Карп/ М.: Просвещение, 2006.
6. Дидактические материалы по алгебре и началам анализа. 10-11 классы. / Б.М. Ивлев и др. / М: Просвещение, 2006
7. Алгебра и начала анализа. Тематические тесты и зачеты. 10-11 классы./Л.О.Денищева, Т.А.Корешкова / М.:Мнемозина, 2003
8. Контрольные и проверочные работы по алгебре. 10-11 классы./Л.И.Звавич, Л.Я. Шляпочник/М.:Дрофа, 1997
9. Устные упражнения по алгебре и началам анализа / Р.Д.Лукин, Т.К. Лукина, И.С. Якунина. М.: Просвещение, 1989
10. Математика. 10-11 классы. Развитие комбинаторно-логического мышления. Задачи, алгоритмы решений / авт.-сост. Т.Г. Попова. Волгоград: Учитель, 2009
11. Математика. 10-11 классы: технология подготовки учащихся к ЕГЭ / авт.-сост. Н.А. Ким. Волгоград: Учитель, 2010
12. Математика. ЕГЭ. Практикум. 2012 г. ( авт. Л.Д. Лаппо, М.А. Попов)
13. Алгебра и начала анализа. Тесты. 10-11 классы: учебно-метод. Пособие. М.: Дрофа, 2010
14. Математика. Подготовка к ЕГЭ – 2012: учебно – методическое пособие /под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов – на – Дону: Легион – М, 2011
15. Решение сложных задач ЕГЭ по математике: 9 – 11 классы. – М.: ВАКО, 2011 (авт. С.И. Колесникова).
Геометрия, 10–11: Учеб. для общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2011.
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 10 кл. – М.: Просвещение, 2009.
Научно-теоретический и методический журнал «Математика в школе»
Ковалева Г.И, Мазурова Н.И. геометрия. 10-11 классы: тесты для текущего и обобщающего контроля. – Волгоград: Учитель, 2006.
Б.Г. Зив, В.М. Мейлер, А.П. Баханский. Задачи по геометрии для 7 – 11 классов. – М.: Просвещение, 2003.
С.М. Саакян, В.Ф. Бутузов. Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2001.
Учимся решать задачи. Геометрия. 10-11 классы. / Л.О.Денищева, Т.Ф.Михеева/М.: ИНТЕЛЛЕКТ-ЦЕНТР, 2000
Геометрия. 10-11 классы. Разрезные карточки по стереометрии./Г.И.Ковалева/Волгоград: Учитель, 2007
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 11 класса. – М. Просвещение, 2009.
Ю.А. Глазков, И.И. Юдина, В.Ф. Бутузов. Рабочая тетрадь по геометрии для 10 класса. – М.: Просвещение, 2011.
В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. Рабочая тетрадь по геометрии для 11 класса. – М.: Просвещение, 2011.
Литература для учащихся.
1. Алгебра и начала математического анализа, 10 11 классы. Учебник для общеобразовательных учреждений /Ш.А. Алимов [и др.], - М.: Просвещение, 2011г.
2. Контрольно-измерительные материалы. Алгебра и начала анализа: 11 класс / сост. А.Н. Рурукин. – М.: ВАКО, 2011
3. Дидактические материалы по алгебре и началам анализа. 10-11 классы. / Б.М. Ивлев и др. / М: Просвещение, 2006
4. Математика. ЕГЭ. Практикум. 2012 г. ( авт. Л.Д. Лаппо, М.А. Попов)
5. Математика. Подготовка к ЕГЭ – 2012: учебно – методическое пособие /под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов – на – Дону: Легион – М, 2011
Геометрия, 10–11: Учеб. для общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2011.
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 10 кл. – М.: Просвещение, 2009.
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 11 класса. – М. Просвещение, 2009.
Ю.А. Глазков, И.И. Юдина, В.Ф. Бутузов. Рабочая тетрадь по геометрии для 10 класса. – М.: Просвещение, 2011.
В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. Рабочая тетрадь по геометрии для 11 класса. – М.: Просвещение, 2011.
Электронные образовательные ресурсы для учителя
Единая коллекция цифровых образовательных ресурсов: http://school-collection.edu.ru/
Средняя математическая интернет-школа (вся элементарная математика): http://www.bymath.net/
Математика в «Открытом колледже»: http://www.mathematics.ru/
Официальный информационный портал ЕГЭ: http://www.ege.edu.ru/
ЕГЭ по математике, подготовка к тестированию по математике: http://uztest.ru/
ЕГЭ по математике: http://ege.yandex.ru/mathematics
Открытый банк заданий по математике (для подготовки к ЕГЭ): http://mathege.ru/or/ege/Main/
Сайт подготовки к ЕГЭ по математике «Математические будни»: http://schoolmathematics.ru/
Педсовет: образование, учитель, школа: http://pedsovet.org/
Сайт федерального института педагогических измерений: http://fipi.ru/
Учительский портал: http://www.uchportal.ru/
Фестиваль педагогических идей «Открытый урок» (преподавание математики): http://festival.1september.ru/articles/subjects/1
Сайт Александра Александровича Ларина (математика, репетитор): http://alexlarin.net/
Сайт учителя математики Елены Михайловны Савченко: http://lesavchen.ucoz.ru/
Электронные образовательные ресурсы для учащихся
Единая коллекция цифровых образовательных ресурсов: http://school-collection.edu.ru/
Средняя математическая интернет-школа (вся элементарная математика): http://www.bymath.net/
Математика в «Открытом колледже»: http://www.mathematics.ru/
Математика в помощь школьнику и студенту (тесты по математике on-line): http://www.mathtest.ru/
Официальный информационный портал ЕГЭ: http://www.ege.edu.ru/
ЕГЭ по математике, подготовка к тестированию по математике: http://uztest.ru/
ЕГЭ по математике: http://ege.yandex.ru/mathematics
Открытый банк заданий по математике (для подготовки к ЕГЭ): http://mathege.ru/or/ege/Main/
Сайт подготовки к ЕГЭ по математике «Математические будни»: http://schoolmathematics.ru/
Сайт федерального института педагогических измерений: http://fipi.ru/
Сайт Александра Александровича Ларина (математика, репетитор): http://alexlarin.net/
График контрольных работ
11а
| № п/п | Тема контрольной работы | Дата
|
| 1 | Входная контрольная работа | 11.100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000009 |
| 2 | Контрольная работа №1 по теме «Тригонометрические функции». | 03.10 |
| 3 | Контрольная работа № 2 по теме «Координаты точки и координаты вектора» | 14.10 |
| 4 | Контрольная работа № 3 по теме «Скалярное произведение векторов. Движения» | 24.10 |
| 5 | Контрольная работа № 4 по теме «Производная и ее геометрический смысл». | 27.11 |
| 6 | Контрольная работа № 5 по теме «Применение производной к исследованию функций». | 22.12 |
| 7 | Контрольная работа №6 по теме «Цилиндр, конус, шар» | 23.01 |
| 8 | Контрольная работа № 7 по теме «Интеграл». | 12.02 |
| 9 | Контрольная работа № 8 по теме «Объемы тел» | 27.02 |
| 10 | Контрольная работа № 9 по теме «Элементы математической статистики, комбинаторики и теории вероятностей». | 20.03 |
| 11 | Контрольная работа № 10 по теме «Комплексные числа» | 07.04 |
| 12 | Итоговая контрольная работа. | 21.05 |
График контрольных работ
11Б
| № п/п | Тема контрольной работы | Дата
|
| 1 | Входная контрольная работа | 10.09 |
| 2 | Контрольная работа №1 по теме «Тригонометрические функции». | 01.10 |
| 3 | Контрольная работа № 2 по теме «Координаты точки и координаты вектора» | 14.10 |
| 4 | Контрольная работа № 3 по теме «Скалярное произведение векторов. Движения» | 23.10 |
| 5 | Контрольная работа № 4 по теме «Производная и ее геометрический смысл». | 26.11 |
| 6 | Контрольная работа № 5 по теме «Применение производной к исследованию функций». | 20.12 |
| 7 | Контрольная работа №6 по теме «Цилиндр, конус, шар» | 22.01 |
| 8 | Контрольная работа № 7 по теме «Интеграл». | 11.02 |
| 9 | Контрольная работа № 8 по теме «Объемы тел» | 27.02 |
| 10 | Контрольная работа № 9 по теме «Элементы математической статистики, комбинаторики и теории вероятностей». | 19.03 |
| 11 | Контрольная работа № 10 по теме «Комплексные числа» | 07.04 |
| 12 | Итоговая контрольная работа. | 21.05 |
24
, 
, 
. 
и ее график.
и ее график.
и её график.
