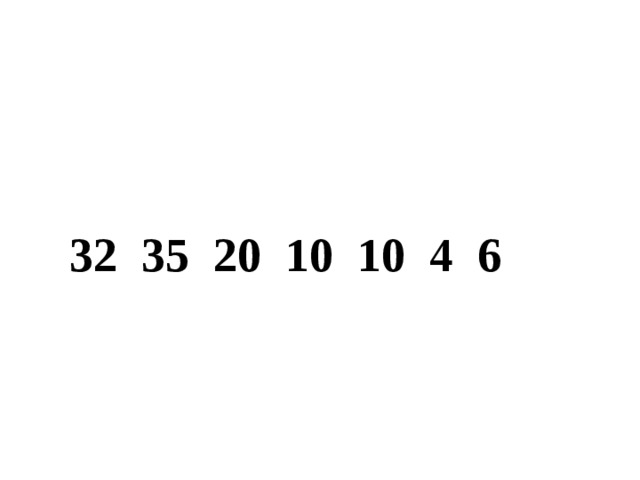Конспект урока математики тема "Нахождение площади прямоугольника"

Среди данных фигур найдите прямоугольники.

3

1

4

5

6

Среди данных фигур найдите прямоугольники.

3

1

4

5

6

Треугольник

Отрезок

Многоугольник

Прямоугольник

Четырехугольник

Квадрат

Треугольник

Отрезок

Многоугольник

Прямоугольник

Четырехугольник

Квадрат

Треугольник

Отрезок

Многоугольник

Прямоугольник

Четырехугольник

Квадрат

Треугольник

Отрезок

Многоугольник

Прямоугольник

Четырехугольник

Квадрат

Треугольник

Отрезок

Многоугольник

Прямоугольник

Четырехугольник

Квадрат

Треугольник

Отрезок

Многоугольник

Прямоугольник

Четырехугольник

Квадрат

Этап урока

Деятельность учителя

Деятельность учащихся

Универсальные учебные действия

1.Мотивирование к учебной деятельности.

– Улыбнитесь друг другу, нашим гостям, мне, ведь: «С маленькой удачи начинается большой успех!»
 Слайд 2: дети читают хором:

– Чтобы вы хотели пожелать сегодня на уроке своему соседу по парте.

–Мы сегодня будем снова раскрывать тайны…математики. Готовы? 
А открытием, которое сегодня сделает каждый из вас, вы поделитесь в конце урока.

Слушают учителя, психологический настрой

Мы – умные! 
  Мы – дружные!
  Мы – внимательные!
  Мы – старательные!
  Мы – отлично учимся!
  Все у нас получится!

Учащиеся высказывают пожелания своему соседу.
– Удачи при решении задач.
– Хорошей работы на уроке. И т.д.

Личностные: самоопределение.

Регулятивные: целеполагание.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

2. Актуализация знаний

1. Самостоятельная работа

(6 + 2) · 4 =
 (13 – 8) · 7 =
  68 – 60 + 12 =
  36 : 6 + 4 =
  (18 – 17) · 10 =

2. Повторение геометрических понятий.

Какие геометрические фигуры вы знаете? 
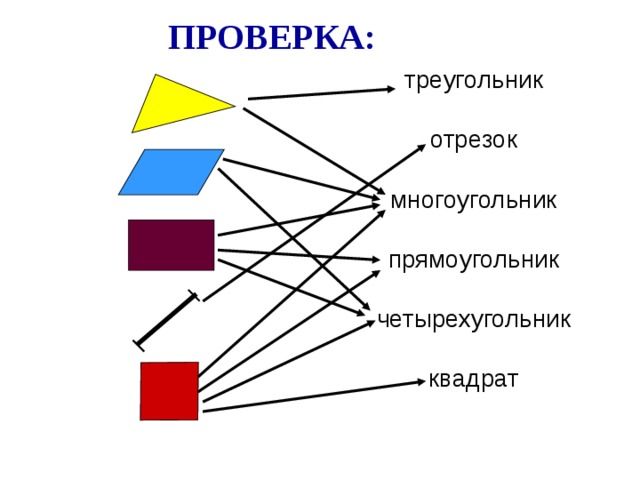
 1) Самостоятельная работа №1 (карточка)

– Соедините фигуры и названия фигур стрелками там, где это возможно.
Слайд 4: Обменяйтесь своими тетрадями, проверьте выполнение задания друг у друга по эталону на слайде.

Слайд 5: Геометрические фигуры 
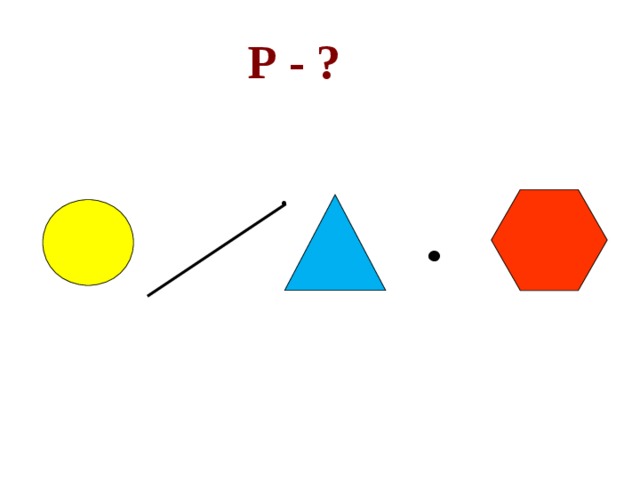
 2) У каких геометрических фигур нельзя определить периметр?

Слайд 6: 
 3) Какие фигуры изображены на слайде? 
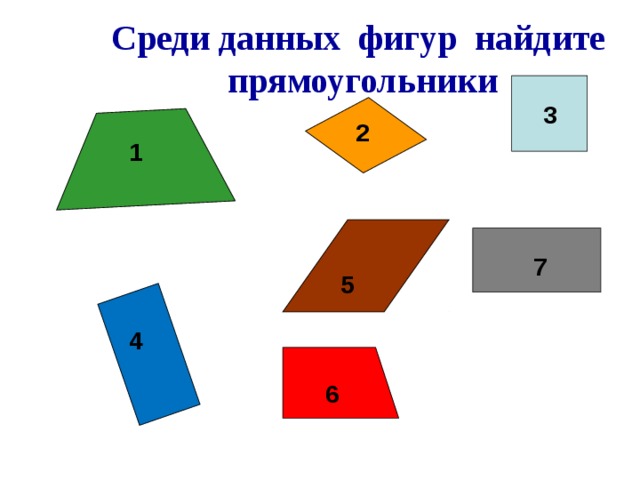
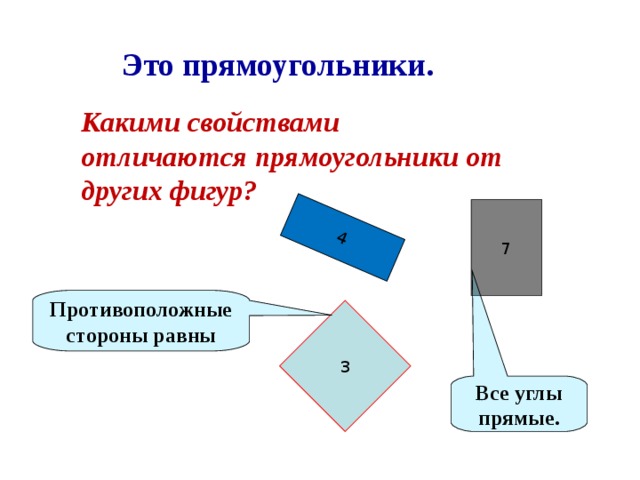
Среди данных фигур найдите прямоугольники. Докажите свой выбор. Слайд 7: 
Какими свойствами отличаются прямоугольники от других фигур?

4) Вспомним алгоритм нахождения периметра.
 5) Задача на нахождение периметра прямоугольника.
Слайд 8: 
 Начертите в тетради прямоугольник со сторонами 4см и 3см. Найдите периметр и площадь этой фигуры.

Ответы: 32 35 20 10 10 4 6

Ответы детей.

Взаимопроверка и взаимоконтроль.

Круг, луч, точка.

Работа в парах.
(карточка)

Называют номер фигуры и доказывают свой выбор: прямые углы, противоположные стороны равны.

Решают задачу на нахождение периметра. Чертят в тетради прямоугольник.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

Познавательные: логические – анализ объектов с целью выделения признаков.

3. Создание проблемной ситуации

Задача на нахождение площади.
 Слайд 9: 
– Проблема: Как найти площадь?

Ребята делают предположения и обосновывают свои ответы.

Регулятивные: целеполагание.
 Коммуникативные: постановка вопросов.
 Познавательные: самостоятельное выделение – формулирование познавательной цели; логические – формулирование проблемы.

4. Формулирование проблемы (темы и цели урока)

– Смогли выполнить задание?
– В чем затруднение?
– Почему мы не выполнили второе задание?
– Какой возникает вопрос?

Слайд 10: тема урока «Площадь прямоугольника»
 – Назовите цель урока.

познакомимся с…

сформируем умения…

развиваем…

воспитываем…

Слайд 11:

1. Как можно сравнить эти фигуры?
     
Вывод: Они имеют одинаковые площади. 
Слайд 12: 
 2. Что можно сказать про площадь треугольника? 
          
Вывод: площадь треугольника меньше площади квадрата.

Слайд 13:

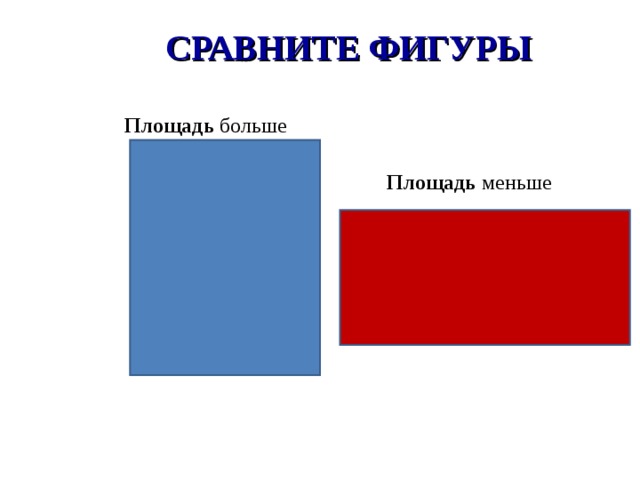
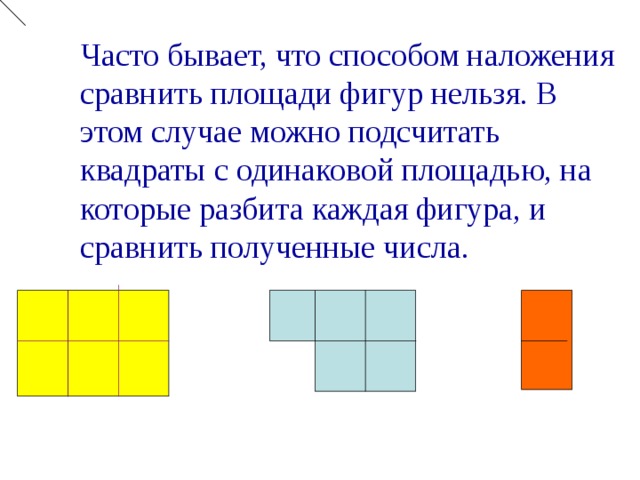
 3. Можно ли на «глаз» или наложением определить, площадь какой фигуры больше?

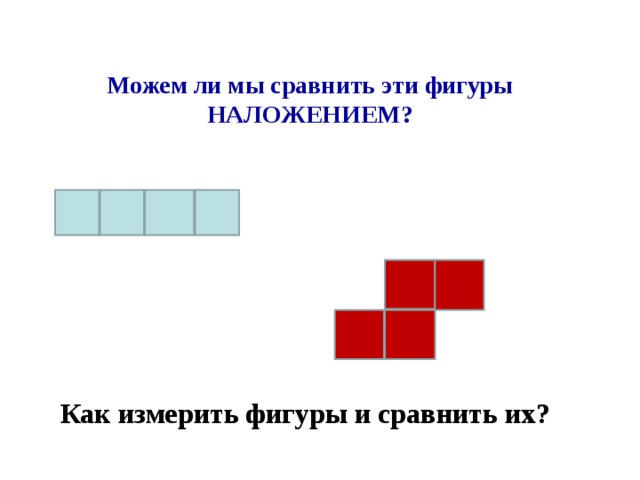
Слайд 14:
– Можем ли мы сравнить эти фигуры наложением? (нет)
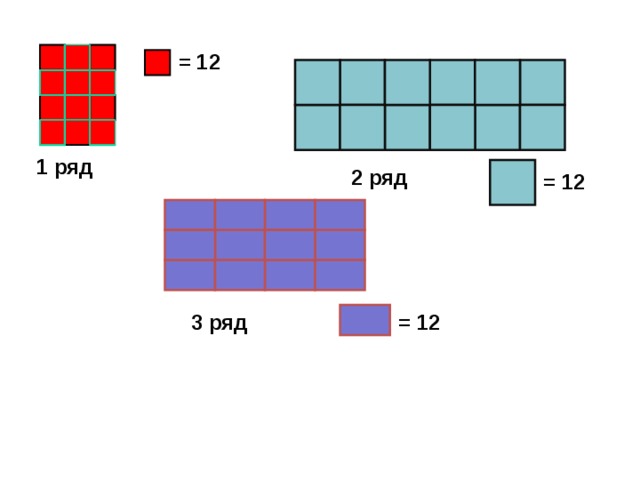
– Как измерить и сравнить фигуры? (Выбирается мерка и устанавливается, сколько раз эта мерка содержится в измеряемой величине)
Слайд 15:
– Сейчас каждая группа получит лист с изображенным на нем прямоугольником и разные мерки (Мерки сделаны из цветной самоклеющейся бумаги. Учащиеся должны в прямоугольник вклеить столько мерок, сколько в него поместится) 
– Что измеряли? (Ответы–предположения)
– Почему, имея разные прямоугольники, мы получили одинаковый результат? (Использовали разные мерки)
– Какое правило себе напомнили? (Сравнивать, складывать и вычитать величины можно только тогда, когда они измерены одинаковыми мерками)

Формулируют учебную проблему.
– Мы не знаем, как найти площадь
– Как найти площадь прямоугольника?

 Пытаются сформулировать цели урока совместно с учителем

Работа в паре

Площадь больше

Работа в группе

Коммуникативные: постановка вопросов.
 Познавательные: самостоятельное выделение – формулирование познавательной цели; логические – формулирование проблемы.

5. Выдвижение гипотез

– Предположите, как можно найти площадь прямоугольника?
Слайд 16: 
– Работаем с одинаковыми мерками! Считаем вместе!

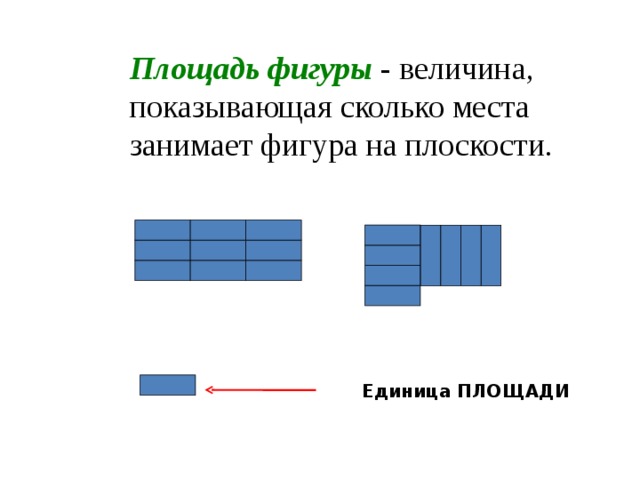
Слайд 17:
Что такое площадь?

Дети высказывают свои предположения

– Разбить прямоугольник на квадратные сантиметры, подсчитать их количество и узнать площади.

Разбивают прямоугольник на квадратные сантиметры. Подсчитывают квадратные сантиметры.

Регулятивные: планирование, прогнозирование.
 Познавательные: моделирование.
 Логические – решение проблемы, построение логической цепи рассуждений, доказательство.
 Коммуникативные :инициативное сотрудничество в поиске и выборе информации.

6.Открытие нового знания

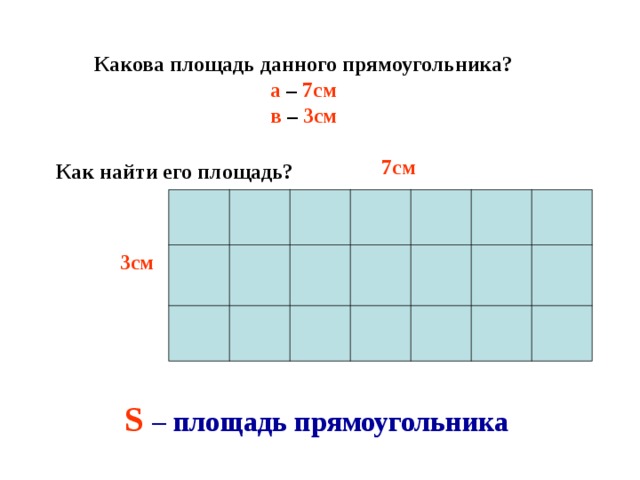
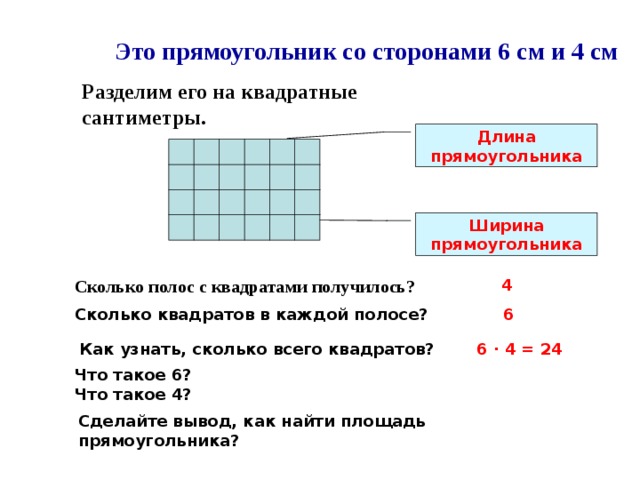
Слайд 18:
–Какова площадь данного прямоугольника? 
– Для выполнения задания потребовалось много времени. Предлагаю найти способ вычисления площади прямоугольника, который позволил бы выполнить эту работу быстрее.

Сосчитайте число квадратов, расположенных в первом ряду по длине прямоугольника.

– Сосчитайте количество таких рядов.

– Как найти площадь не расчерчивая каждый раз на квадратные сантиметры?
S – площадь прямоугольника

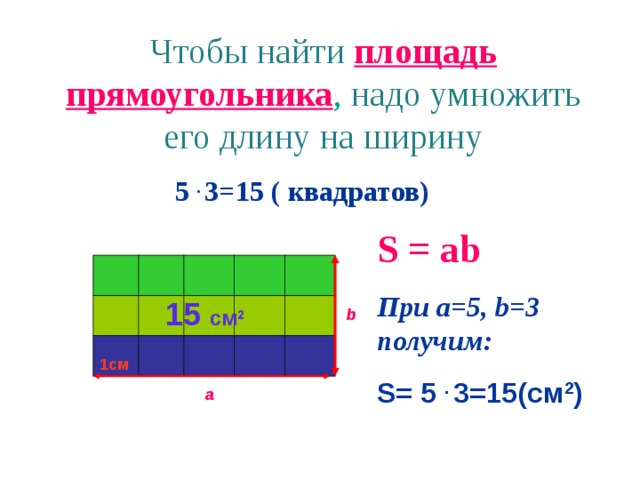
Слайд 19:
Формула площади

Слайд 20: 
В качестве общепринятых единиц измерения площадей используют квадраты со сторонами 1 см, 1 дм, 1 м.
Эти измерения называют соответственно:
квадратный сантиметр – 1 см²
квадратный дециметр – 1 дм²
квадратный метр – 1 м²

– Их количество равно длине прямоугольника.

– Их количество равно ширине прямоугольника.
– Для нахождения площади прямоугольника надо длину умножить на ширину.

Дети делают вывод, о нахождении площади прямоугольник

Составление алгоритма в группе

Регулятивные: контроль, оценка, коррекция.
 Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач; рефлексия способов и условий действия.

Коммуникативные: управление поведением партнера – контроль, коррекция, оценка действий партнера.

7. Формулирование нового знания 
 .

Слайд 21: 
Прочитайте правило нахождения площади прямоугольника.

– Обозначим площадь буквой S, длину – буквой a, ширину – буквой b. Записать правило в виде формулы.

Знакомство с правилом: «Чтобы найти площадь прямоугольника, надо длину умножить на ширину».

Делают вывод: S = a•b

Составление алгоритма в группе

8. Физминутка

«Мы – чертёжники».
– Начертите глазами луч (на стене найдите точку и отправьте луч далеко сквозь окно), кончиком носа – окружность, правой рукой– прямой угол, а левой– острый! Чертите аккуратно! Левой ногой – квадрат, а правой прямоугольник.

9. Применение нового знания

Площадь какой фигуры мы учились находить?
Как найти площадь прямоугольника? 
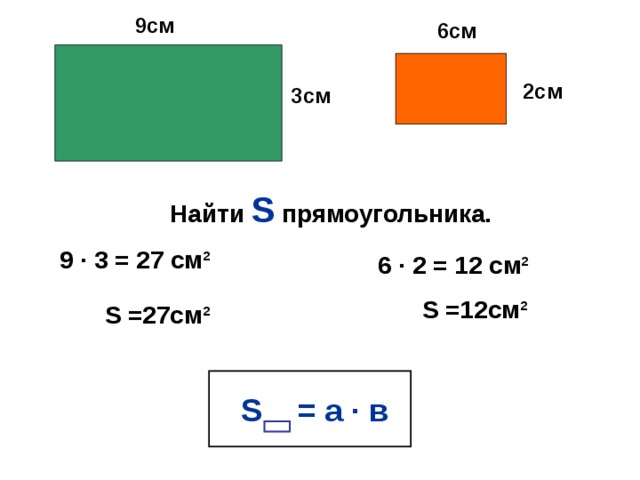
Слайды 22,23: 
 Анализирует результаты выполнения учащимися задания
Определите площади прямоугольных полей

Выполняют задание самостоятельно

Называют с помощью учителя место своего затруднения, причину исправляют ошибки.

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
Личностные: самоопределение.

10. Повторение и закрепление полученного ранее.

1. Давайте решим задачу в учебнике на стр.57 №4

Решают задачу

Регулятивные: контроль, коррекция.
Личностные: самоопределение.

9. Домашнее задание

Дает инструктаж по выполнению домашнего задания. 
Начертите две разные фигуры, но только так, чтобы площадь у них была одинаковой. Подумать, какую формулу можно применить для нахождения площади.

Знакомятся с заданием, слушают инструкцию

10. Рефлексия деятельности.

Какое открытие вы сделали на уроке?

– Назовите цель нашего урока.

– Какое задание было для вас самым интересным? Самым трудным?

– Где в реальной жизни может возникнуть необходимость вычислить площадь прямоугольника?

Отвечают на вопросы

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли.
Познавательные: рефлексия.