Подготовительный этап |
| Деятельность учителя | Деятельность учеников | Примечания |
| - Здравствуйте, садитесь! Прежде, чем начать урок, рассядьтесь, пожалуйста, согласно рассадке, написанной в журнале. - Но прежде, чем перейти к дальнейшему закреплению данной темы при решении задач давайте вспомним теорию, которая была задана вам на дом. Закрываем учебники! - …, иди к доске. Сделай рисунок и сформулируй нам теорему о свойстве биссектрисы угла. - …, иди к доске. Сделай рисунок и сформулируй нам теорему о точке пересечения биссектрис. - …, что называется биссектрисой? - Каким свойством обладают серединные перпендикуляры, проведенные к сторонам треугольника? - Класс, кто может сформулировать теорему о свойстве прямых, содержащих высоты треугольника. -…, ты внимательно слушал, повтори теорему еще раз.
| Ученики приветствуют учителя
Внимательно слушают
Отвечают на вопросы Когда кто – то рассказывает теорему у доски – внимательно слушают, поправляют
|
На доске приведены рисунки
В то время, как кто-то выполняет рисунок, учитель повторяет основные понятия: биссектриса, медиана, высота, серединный перпендикуляр |
Ориентировочный этап |
| - Самые красивые теоремы в геометрии связаны именно с этими точкам. И вы с ними уже знакомы. Что же это за точки? - Итак, сегодня мы продолжим изучение темы: «Замечательные точки треугольника». Откройте тетради и запишите: число, классная работа. - На следующей неделе вы будете писать контрольную работу по этой теме. Любая из решенных сегодня задач может быть включена в эту контрольную. Если у вас будут возникать вопросы, тихонько подымите руку. - Обратите внимание на доску. На протяжении всего урока мы будем решать примеры, которые записаны на левой доске и отделены чертой. Те, кто будут решать задачи быстрее всех, могут переходить к решению следующих задач, если последующие задачи будут решены верно, вы заслуженно получите хорошую оценку. |
Внимательно слушают Отвечают на вопрос
Записывают в тетради: число, классная работа, тема. Внимательно слушают
Внимательно слушают |
В это время учитель проверяет наличие у уч-ся учебных принадлежностей
В классе две доски. Примеры, которые запланировано решить на уроке, записаны на второй доске и отделены чертой |
Исполнительный этап |
| - На прошлом уроке мы начали решать задачу №78, но не довели ее до конца. Я расскажу вам идею решения, а вы самостоятельно запишите решение в тетради. - Для решения задачи нам необходимо знать формулу, по которой измеряется площадь треугольника… | Внимательно слушают. Отвечают на вопросы учителя. Записывают решение в классные тетради. | №78 Рисунок заранее сделан с обратной стороны левого крыла доски для экономии времени, так как данный рисунок есть в тетрадях уч-ся
|
| Решение задачи № 78 |
| Решение: Проведем ОН перпендикулярно АВ Так как треуг.АВС – равнобедренный, то АТ – биссектриса, медиана и высота. � �АВС по теореме о свойстве биссектрисы угла ОН = ОТ. �АВС по теореме о свойстве биссектрисы угла ОН = ОТ. S = ½*ОН*АВ =ОН = 2* S/АВ= 2*35/14 = 5 см. ОТ = ОН = 5 см. Ответ: 5 см.
| Дано: тр. АВС, АВ = АС, ВF, AT – биссектрисы, ВF пер. AT = О, АВ = 14 см. S = 35 см(2). = 35 см(2). Найти: ОТ
| А
 
 
F   14 cм.
  Н
O

В С T
|
| - Переходим к решению следующей задачи. Для решения следующей задачи нам понадобиться теорема о точке пересечения биссектрис. - …, сформулируй данную теорему. -…, иди к доске, напиши, что дано в задаче и выполни рисунок. | Внимательно слушают
Отвечают на наводящие вопросы Решают задачу Один ученик решает задачу у доски, остальные записывают решение рабочие тетради | №80 Учитель постоянно акцентирует внимание уч-ся на доску |
| Решение задачи № 80 |
| Решение: Так как биссектрисы треугольника пересекаются в одной точке, то ВО – биссектриса � �АВС, т.е � �АВС, т.е �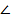 �АВО = � �АВО = �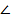 �ОВС. �ОВС. Сумма всех углов треугольника равна 180° = 2�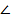 �АВО + 2� �АВО + 2�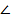 �ОСВ + 2� �ОСВ + 2�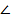 �ОАС = 180° = � �ОАС = 180° = �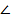 �АВО + � �АВО + �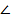 �ОСВ + � �ОСВ + �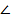 �ОАС = 90° = �ОАС = 90° = �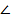 �АВО = 90°- � �АВО = 90°- �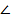 �ОСВ - � �ОСВ - �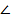 �ОАС = 90°-22°-31°= �ОАС = 90°-22°-31°= Ответ: 37°. | Дано: треугольник АВС, СF, AT – биссектрисы, СF пер. AT = О, �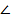 �ОАС = 31° �ОАС = 31° �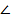 �ОСВ = 22° �ОСВ = 22° Найти: �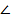 �АВО. �АВО.
|
В
F T
 O 
 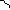 
С А
|
| - Хорошо, с этой задачкой вы справились. На дом вам была заданна задача, которую можно решить знаю теорему о точке пересечения серединных перпендикуляров к сторонам треугольника. Поднимите руки те, кто справился с домашним заданием. А сейчас поднимите руки те, у кого не получилась данная задача. Ну что ж разберем эту задачу. Есть желающие пойти к доске. -…, иди к доске! Во время объяснения учеником решения задачи, учитель комментирует каждую строчку, ссылаясь на свойства и признаки в геометрии, которые необходимы для решения этой задачи | Внимательно слушают, поочередно поднимают руки
Один ученик решает данную задачу на доске, остальные записывают решение в тетради Те, кто решил данную задачу дома, переходит к решению следующей задачи | Рисунок заранее сделан с обратной стороны правого крыла доски для экономии времени, так как данный рисунок есть в учебнике учащихся
|
| Р T ешение задачи № 80 |
| Решение: Так как АВСD - параллелограмм, то ВС = АD = 2 АF FТ перп. АВ = FТ – высота тр. АFВ, АТ = ТВ = FТ – медиана тр. АFВ. = FТ – и медиана, и высота, то треугольник АFВ – равнобедренный, т.е. АF = ВF, 3. ВF = АF = АD/2 = ВС/2 = 18/2 = 9 Ответ: 9 см. | Дано: АВСD - параллелограмм, FT – серединный перпендикуляр, АF = FD, ВС = 18 см. Найти: ВF.
| В А   
 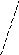
F 18 см.
С l D
|
| - А сейчас немного передохнем. Возьмите лист бумаги и нанесите на нем девять точек так, чтобы они расположились в форме квадрата (учитель в это время изображает эти точке на доске для наглядности). Перечеркните теперь все точки четырьмя прямыми линиями, не отрывая карандаша от бумаги.
- Немного передохнули? Ну что ж, продолжим работу. - Запишите в тетради следующий номер - № 92. - К доске пойдет …. Запиши, что дано в задаче и приступай к решению задачи, остальные самостоятельно решают задачу в рабочих тетрадях. | Внимательно слушают
Думают, предлагают свои идеи Пробуют разрешить поставленную задачу
Самостоятельно решают задачу |
Дано: Решение:  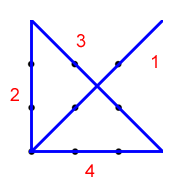
Рисунок выполняется учителем (для экономии времени, так как данный рисунок есть в учебнике) в то время как ученик записывает дано к задаче
|
| Решение задачи № 92 |
| Решение: тр. АОТ подобен тр. FОС по двум углам (�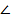 �АОТ = углу СОF –вертикальные, � �АОТ = углу СОF –вертикальные, �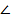 �АТО = � �АТО = �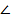 �СFО = 90°) = АТ/FС = ОА/ОС �СFО = 90°) = АТ/FС = ОА/ОС Ответ: 8 см. | Дано: треугольник АВС - остроугольный, АF, СT – высоты, АF пер. СT = О, АТ/FС = 1/2, АО = 4 см. Найти: ОС.
|
В

F

T O

С А
|
| - Для того чтобы решить данную задачу нам необходимо знать: признаки подобия треугольников и определение высоты. | Внимательно слушают | Номера задач для тех, кто решает быстрее остальных: № 82, 85, 91 |
Контрольно – оценочная часть |
| - Итак, подведем итог сегодняшнего урока! Какие замечательные точки вы знаете? - Сформулируйте теоремы. - Верно ли, что точка пересечения серединных перпендикуляров к сторонам треугольника равноудалена от его вершин? - Для чего мы изучаем замечательные точки треугольника? | Отвечают на вопросы
Высказывают свое мнение |
|
Комментированная постановка домашнего задания |
| - Дома вам необходимо повторить §1, 2, 3, так как на следующей неделе вы напишите контрольную работу по этой теме. Также, необходимо решить задачи, которые я вам сейчас раздам. Задачи, которые вам необходимо решить дома могут быть включены в контрольную работу. Домашнее задание написано на правом крыле доски. | Внимательно слушают, открывают дневники и записывают домашнее задание, при этом слушают внимательно комментарии учителя | Учитель раздает карточки с домашним заданием:
Домашнее задание на 15.10.2012 по темам «Касательная к окружности», « Центральные и вписанные углы», « Замечательные точки треугольника » Задача 1. Отрезок ВС – гипотенуза прямоугольного треугольника АВС (рис.1). Верно ли, что прямая АВ является касательной к окружности � �(С; АС)? �(С; АС)? З адача 2. Диагонали ромба АВСD пересекаются в точке О. Окружность, центром которой является точка О, касается сторон ромба, а стороны ВС – в точке К. Вычислите длину радиуса окружности, если ВD = 10 см, ВК = 4 см. адача 2. Диагонали ромба АВСD пересекаются в точке О. Окружность, центром которой является точка О, касается сторон ромба, а стороны ВС – в точке К. Вычислите длину радиуса окружности, если ВD = 10 см, ВК = 4 см. Задача 3. Дана окружность, центром которой является точка О. Прямые АВ и ВС – касательные к окружности, точки А и С – точки касания. Точка Р – точка пересечения окружности с отрезком ОВ, �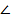 �АВТ = 30°. Докажите, что точка Р является точкой пересечения биссектрис треугольника АВС. �АВТ = 30°. Докажите, что точка Р является точкой пересечения биссектрис треугольника АВС.
Учитель контролирует, чтобы домашнее задание было записано у каждого |
Рефлексия учащихся путём самооценки возможностей по выполнению домашнего задания |
| - Вам розданы листочки, на которых нарисованы окружности, как в игре дарц, поставьте баллы в секторах соответствующие вашей оценки указанных вопросов. После того, как заполните листочки, положите их на край стола. Урок окончен!
Спасибо за активную работу на уроке! До свидания!
| Делают то, что им предложил учитель
Прощаются, уходят | Раздаточный материал:
Доволен своей работой на уроке
На уроке мне было интересно 
Материал урока понятен          Домашнее задание мне кажется не тяжелым 
|





 4
4  2
2 5
5 = 35 см(2).
= 35 см(2).