В этой работе детально рассматривается место замечательных точек треугольника , их роль в решении геометрических задач. Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.
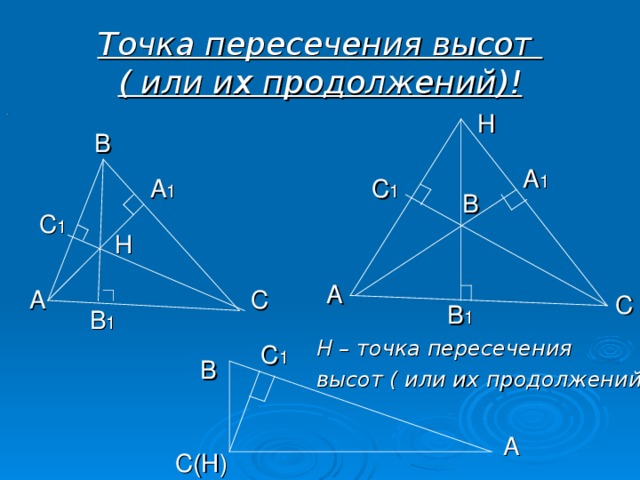
Обычно они расположены внутри треугольника, но и это не обязательно. В частности, точка пересечения высот может находиться вне треугольника.
Замечательными точками треугольника являются
- Точки пересечения:
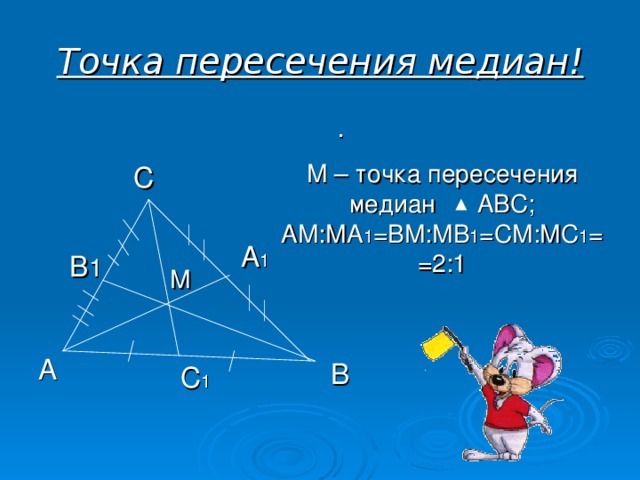
- Медиан — центроид, центр тяжести (масс);
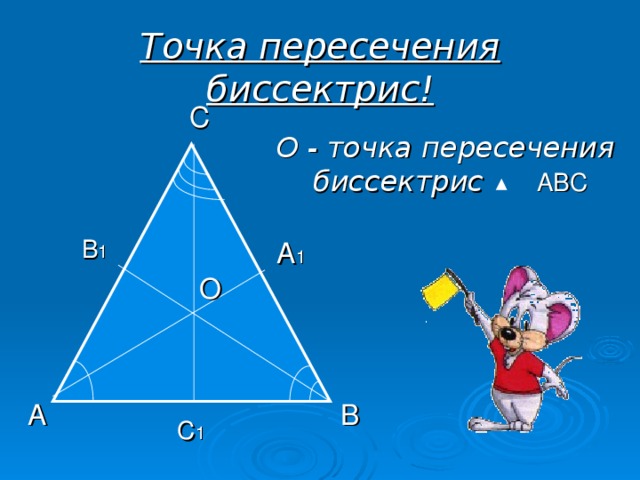
- Биссектрис — инцентр, центр вписанной окружности;
- Высот — ортоцентр;
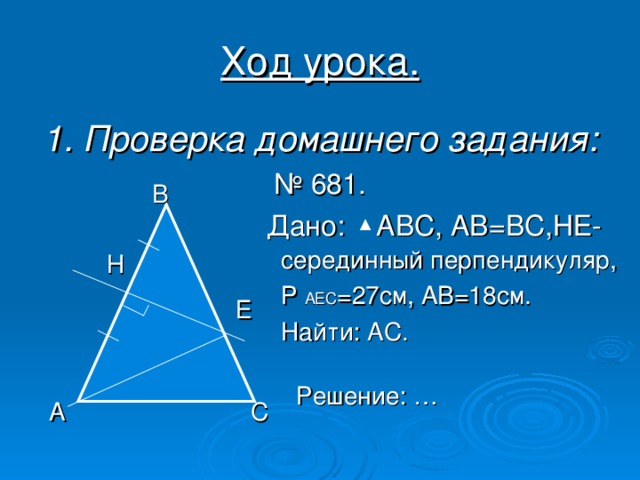
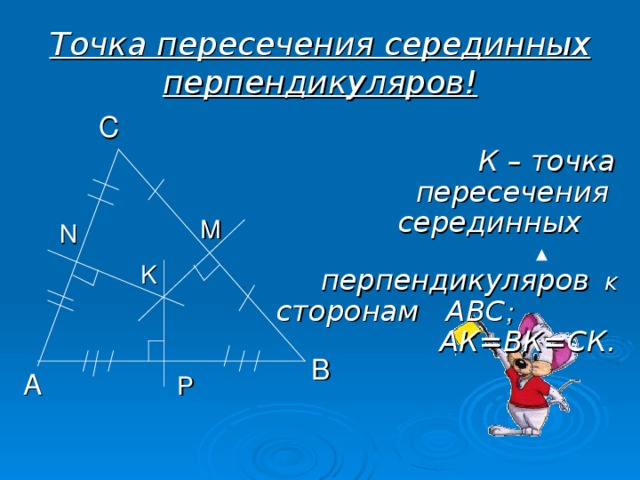
- Серединных перпендикуляров — центр описанной окружности;
- Симедиан — точка Лемуана;
- Биссектрис серединного треугольника (его инцентра) — точка Шпикера;
- Отрезков, соединяющих вершины треугольника:
- c точками касания противоположных сторон и вписанной окружности — точка Жергонна;
- c точками касания противоположных сторон и вневписанных окружностей — точка Нагеля;
- c соответствующими свободными вершинами равносторонних треугольников, построенных на сторонах треугольника (наружу) — первая точка Торричелли
- с соответствующими свободными вершинами правильных треугольников, построенных внутрь треугольника — вторая точка Торричелли.
- c соответствующими свободными вершинами треугольников, подобных исходному треугольнику и построенных на его сторонах — точки Брокара;
- Центр окружности девяти точек.