Методическое приложение к уроку геометрии в 9 классе к разделу: «Соотношения между сторонами и углами треугольника»
Тема урока – «Вычисление площади треугольника по двум сторонам и углу между ними».
(Урок разработан на основе программы и УМК учебника “Геометрия 7-9” авторов Л. С. Атанасян, В. Ф. Бутузов)
Цель урока: доказать теорему о площади треугольника, попробовать на практике применить теорему к решению задач.
Задачи урока:
Обучающая: повторить определения sin и cos, формулы площади треугольника изученные ранее, подтвердить теорему о площади треугольника экспериментальным путем.
Развивающая: развивать внимание, память, логическое мышление; активизировать мыслительную деятельность, умение анализировать, обобщать и рассуждать;
Воспитывающая воспитание трудолюбия, усердия в достижении цели, интерес к предмету.
Тип урока: ознакомление с новым материалом.
Методы работы на уроке:
- проблемный
- частично - поисковый (при выполнении лабораторной работы)
- объяснительно - иллюстративный (при устном счете, выводе теоремы о площади треугольника, проверке решения задач)
- репродуктивный, конструктивный (при выполнении упражнений).
Оборудование: проектор, ИД, карточки для лабораторной работы.
Программное обеспечение :SmartNotebook 10, «Живая математика».
Авторские комментарии: При подготовке материала были использованы следующие возможности
ПО SmartNotebook10:
- Использованы навигационные кнопки для удобства перемещения между страницами.
- Использование ссылок на объект.
- Вставка картинок.
- Использование различных инструментов ПО SmartNotebook10
ПО «Живая математика»:
- Построение треугольника по трем точкам.
- Построение внутренней области.
- Измерение длин отрезков, угла.
- Функция «Вычислить» для нахождения площадь треугольника.
План урока:
- Организационный момент, домашнее задание (3 мин.)
- Устная работа (10 мин.)
- Подготовительный этап (8 мин.)
- Изучение теоретического материала (7 мин.)
- Закрепление, лабораторная работа (15 мин.)
- Итог урока (2 мин.)
Ход урока:
1. Организационный момент: (слайд 1,7)
Учитель сообщает ученикам план сегодняшнего урока. Просит записать домашнее задание в дневник, (учащиеся слушают план на урок и записывают в дневник домашнее задание ).
Ранее мы узнали, как вычислять площадь треугольника через его высоту.
Сегодня мы выведем формулу для вычисления площади треугольника через синус его угла, поработаем устно и в конце урока предстоит лабораторная работа в ПО «Живая математика».
2. Устная работа: (слайд 2,3,4)
Идет с помощью ИД. Учащиеся вспоминают ранее известные формулы площади треугольника, понятия sin и cos угла, решают задания на применения этих понятий на ИД. (Учащиеся выполняют задания на ИД)
3. Подготовительный этап: (слайд 5)
На ИД записаны 4 задачи на вычисления площади треугольника:
-если известно три стороны;
-если известна сторона и высота;
-если прямоугольном треугольнике известна сторона и один угол равен 600;
- если известны длины двух его сторон и угол между ними.
(учащиеся решают задачи в тетради, проверяют правильность решения на ИД)
В решении последней задачи возникает проблема ,т.к. задача на данном этапе пока не решается. Значит необходимо рассмотреть новое понятие или новую формулу, то есть нужно рассмотреть новую теорему о площади треугольника.
4. Изучение теоретического материала:
Учитель задаёт наводящие вопросы, учащиеся отвечают с места:
-Что нового в условии этой задачи по сравнению с предыдущими задачами?
( Даны две стороны треугольника и угол между ними. Найти площадь треугольника)
- Это другой тип задачи? (да)
-Сформулируйте тему урока. (Вычисление площади треугольника по двум сторонам и углу между ними )
-А площадь треугольника как мы вычисляли в предыдущих трех задачах (по формулам)
-Значит, что нам нужно вывести для решения новой задачи (формулу)
-А, чтобы эту формулу можно было применить для любых данных, что мы должны сделать? ( доказать)
-Значит, мы должны доказать теорему.
Учащиеся записывают тему урока и последующие записи в тетрадь. Учитель работает на доске.
Тема: «Теорема о площади треугольника»
Формулировка теоремы:
«Площадь треугольника равна половине произведения двух его сторон на синус угла между ними».
Запишем эту теорему в стандартных для треугольника обозначениях.
Напомним эти стандартные обозначения.
Вершина А: угол a, противолежащая сторона а.
Вершина В: угол b, противолежащая сторона в.
Вершина С: угол с, противолежащая сторона с.
Доказательство:
способ- аналитический
АС. ВН 2) ВН =АВ. Sin А
3) S = АС.АВ Sin А
Как ожно записать теорему по другому ? (учащиеся записывают свои варианты)
S = а в SinС , S = а с SinВ
А теперь вернемся и решим 4 задачу. (Учащиеся решают 4 задачу в тетрадях, один ученик на доске, проверяем правильность ответа).
5. Закрепление, лабораторная работа: (слайд 6)
Учащиеся получают индивидуальные карточки для лабораторной работы и приступают к выполнению задания в ПО «Живая математика». Задания выполняют в полученных листах. По окончанию работы делают вывод и сдают свою работу на проверку учителю.
В зависимости от технического обеспечения класса эта работа может проходить в нескольких вариантах: индивидуально, в группах 2-3 человек, и все вместе на ИД.
6.Итог урока:
Итак, мы доказали теорему о площади треугольника через синус его угла.
На следующем уроке мы выведем важную теорему синусов.
-Проанализируйте свою работу на уроке, заполнив карточку.
(учащиеся получают карточку и заполняют её)
Карточка для этапа рефлексии
Ответьте на вопросы:
- Данная тема мне понятна.
- Я хорошо понял теорему о вычислении площади треугольника по двум сторонам и углу между ними
- Я знаю, как пользоваться формулой для вычисления площади треугольника по двум сторонам и углу меду ними
- Я сумею найти______________________________________________________
- В лабораторной работе у меня все получилось_________________________
- Я понял теорему, но в лабораторной работе на уроке допустил ошибки при вычислении__________________________________________________________
- Я доволен своей работой на уроке_______________________________________
2-3 человека озвучивают свой анализ деятельности на уроке, по желанию.
Домашнее задание (даётся в начале уроке)
П.96, № 1020(в), 1021,1024( а или б по выбору учащегося)
Просмотр содержимого документа
«Конспект урока»
Маслова Лидия Сергеевна
МКОУ Октябрьская СОШ №9, Богучанский район
Методическое приложение к уроку геометрии в 9 классе к разделу: «Соотношения между сторонами и углами треугольника»
Тема урока – «Вычисление площади треугольника по двум сторонам и углу между ними».
(Урок разработан на основе программы и УМК учебника “Геометрия 7-9” авторов Л. С. Атанасян, В. Ф. Бутузов)
Цель урока: доказать теорему о площади треугольника, попробовать на практике применить теорему к решению задач.
Задачи урока:
Обучающая: повторить определения sin и cos, формулы площади треугольника изученные ранее, подтвердить теорему о площади треугольника экспериментальным путем.
Развивающая: развивать внимание, память, логическое мышление; активизировать мыслительную деятельность, умение анализировать, обобщать и рассуждать;
Воспитывающая воспитание трудолюбия, усердия в достижении цели, интерес к предмету.
Тип урока: ознакомление с новым материалом.
Методы работы на уроке:
проблемный
частично - поисковый (при выполнении лабораторной работы)
объяснительно - иллюстративный (при устном счете, выводе теоремы о площади треугольника, проверке решения задач)
Оборудование: проектор, ИД, карточки для лабораторной работы.
Программное обеспечение :SmartNotebook 10, «Живая математика».
Авторские комментарии: При подготовке материала были использованы следующие возможности
ПО SmartNotebook10:
Использованы навигационные кнопки для удобства перемещения между страницами.
Использование ссылок на объект.
Вставка картинок.
Использование различных инструментов ПО SmartNotebook10
ПО «Живая математика»:
Построение треугольника по трем точкам.
Построение внутренней области.
Измерение длин отрезков, угла.
Функция «Вычислить» для нахождения площадь треугольника.
План урока:
Организационный момент, домашнее задание (3 мин.)
Устная работа (10 мин.)
Подготовительный этап (8 мин.)
Изучение теоретического материала (7 мин.)
Закрепление, лабораторная работа (15 мин.)
Итог урока (2 мин.)
Ход урока:
1. Организационный момент: (слайд 1,7)
Учитель сообщает ученикам план сегодняшнего урока. Просит записать домашнее задание в дневник, (учащиеся слушают план на урок и записывают в дневник домашнее задание ).
Ранее мы узнали, как вычислять площадь треугольника через его высоту.
Сегодня мы выведем формулу для вычисления площади треугольника через синус его угла, поработаем устно и в конце урока предстоит лабораторная работа в ПО «Живая математика».
2. Устная работа: (слайд 2,3,4)
Идет с помощью ИД. Учащиеся вспоминают ранее известные формулы площади треугольника, понятия sin и cos угла, решают задания на применения этих понятий на ИД. (Учащиеся выполняют задания на ИД)
3. Подготовительный этап: (слайд 5)
На ИД записаны 4 задачи на вычисления площади треугольника:
-если известно три стороны;
-если известна сторона и высота;
-если прямоугольном треугольнике известна сторона и один угол равен 600;
- если известны длины двух его сторон и угол между ними.
(учащиеся решают задачи в тетради, проверяют правильность решения на ИД)
В решении последней задачи возникает проблема ,т.к. задача на данном этапе пока не решается. Значит необходимо рассмотреть новое понятие или новую формулу, то есть нужно рассмотреть новую теорему о площади треугольника.
4. Изучение теоретического материала:
Учитель задаёт наводящие вопросы, учащиеся отвечают с места:
-Что нового в условии этой задачи по сравнению с предыдущими задачами?
( Даны две стороны треугольника и угол между ними. Найти площадь треугольника)
- Это другой тип задачи? (да)
-Сформулируйте тему урока. (Вычисление площади треугольника по двум сторонам и углу между ними )
-А площадь треугольника как мы вычисляли в предыдущих трех задачах (по формулам)
-Значит, что нам нужно вывести для решения новой задачи (формулу)
-А, чтобы эту формулу можно было применить для любых данных, что мы должны сделать? ( доказать)
-Значит, мы должны доказать теорему.
Учащиеся записывают тему урока и последующие записи в тетрадь. Учитель работает на доске.
Тема: «Теорема о площади треугольника»
Формулировка теоремы:
«Площадь треугольника равна половине произведения двух его сторон на синус угла между ними».
Запишем эту теорему в стандартных для треугольника обозначениях.
Напомним эти стандартные обозначения.
Вершина А: угол a, противолежащая сторона а.
Вершина В: угол b, противолежащая сторона в.
Вершина С: угол с, противолежащая сторона с.
Доказательство:
способ- аналитический
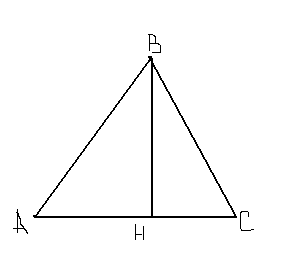
1)S = 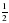 АС. ВН 2) ВН =АВ. Sin А
АС. ВН 2) ВН =АВ. Sin А
3) S = 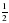 АС.АВ Sin А
АС.АВ Sin А
Как можно записать теорему по другому ? (учащиеся записывают свои варианты)
S = 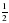 а в SinС , S =
а в SinС , S = 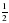 а с SinВ
а с SinВ
А теперь вернемся и решим 4 задачу. (Учащиеся решают 4 задачу в тетрадях, один ученик на доске, проверяем правильность ответа).
5. Закрепление, лабораторная работа: (слайд 6)
Учащиеся получают индивидуальные карточки для лабораторной работы и приступают к выполнению задания в ПО «Живая математика». Задания выполняют в полученных листах. По окончанию работы делают вывод и сдают свою работу на проверку учителю.
В зависимости от технического обеспечения класса эта работа может проходить в нескольких вариантах: индивидуально, в группах 2-3 человек, и все вместе на ИД.
6.Итог урока:
Итак, мы доказали теорему о площади треугольника через синус его угла.
На следующем уроке мы выведем важную теорему синусов.
-Проанализируйте свою работу на уроке, заполнив карточку.
(учащиеся получают карточку и заполняют её)
Карточка для этапа рефлексии
Ответьте на вопросы:
Данная тема мне понятна.
Я хорошо понял теорему о вычислении площади треугольника по двум сторонам и углу между ними
Я знаю, как пользоваться формулой для вычисления площади треугольника по двум сторонам и углу меду ними
Я сумею найти______________________________________________________
В лабораторной работе у меня все получилось_________________________
Я понял теорему, но в лабораторной работе на уроке допустил ошибки при вычислении__________________________________________________________
Я доволен своей работой на уроке_______________________________________
2-3 человека озвучивают свой анализ деятельности на уроке, по желанию.
Домашнее задание (даётся в начале уроке)
П.96, № 1020(в), 1021,1024( а или б по выбору учащегося)


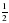 АС. ВН 2) ВН =АВ.
АС. ВН 2) ВН =АВ. 















