Возрастание и убывание функции

Тема урока :

«Признак возрастания и убывания функции»

Очеретина Татьяна Владимировна,
учитель математики первой квалификационной категории

школы № 135 Кировского района города Казани

Основная цель: обобщение знаний и умений учащихся по данной теме, рассмотрев область определения и значения функции, четность и нечетность функции, нулей функции, промежутки монотонности функции;

осуществление контроля определенных знаний и умений по теме «Возрастание и убывание функции»;

формирование познавательного интереса к предмету через использование нестандартных ситуаций и инновационных технологий;

развитие понимания, внимания и математического мышления;

подготовить учащихся к сдаче ЕГЭ .

Метод преподавания: стимулирующий.

Метод учения: частично – поисковый.

Цели урока:

Познавательные:

- выработать навыки решения заданий на область определения и значения функции, четность и нечетность функции, нулей функции, промежутки монотонности функции;

- организация усвоения материала через использование нестандартных ситуаций;

- углубление понимания сущности материала;

- отработка навыков, закрепление изученного материала;

- установление новых связей между понятиями;

- обобщение и систематизация знаний.

Развивающие:

- умение анализировать и устанавливать причинно- следственные связи;

- умение обобщать, наблюдать и сопоставлять;

- умение переносить знания в новую ситуацию;

- перенос знаний и умений в различные ситуации;

- формирование научности мировоззрения.

Воспитывающие:

- воспитание познавательного интереса к уроку;

- формирование умения самоконтроля ;

- воспитывать умение работать в коллективе;

- воспитывать внимательное отношение к одноклассникам;

- способствовать эстетическому воспитанию школьников;

- содействовать профилактике утомляемости, использовать специальные приемы поддерживания работоспособности.

Необходимые ресурсы и материалы:

АРМ (автоматизированное рабочее место),

минимальные системные требования: Windows XP с установленным Microsoft Office,

раздаточный материал – тестовые работы №1,2,3,4 (в печатном виде)

Структура урока:

I этап. Сообщение темы целей, задач урока и мотивация учебной деятельности.

Сегодня мы вспомним ранее изученные свойства функций : область определения и значения функции, четность и нечетность функции, нули функции, промежутки возрастания и убывания функции на конкретном примере. Проверим свои знания и умения тестовым контролем и рассмотрим необходимые и достаточные условия возрастания и убывания функции, научимся находить промежутки монотонности с помощью производной, разберем решение одного из возможных заданий ЕГЭ.

II этап. Подготовка к изучению новой темы через актуализацию опорных знаний (устно –на экране), проведение тестовых работ с проверкой на экране.

III этап. Осмысление и закрепление нового материала.

IV этап. Постановка задачи для выполнения одного их возможных заданий ЕГЭ.

V этап. Подведение итогов исследования . Выводы..

Тема урока:

Признак возрастания и убывания функции

11 класс

Учитель первой категории школы №135

Кировского района г. Казани

Очеретина Татьяна Владимировна

Начнем

урок!

y

7

6

5

4

3

F(x)

2

1

x

1 2 3 4 5 6 7

-1

-7 -6 -5 -4 -3 -2 -1

-2

-3

-4

-5

-6

-7

1 2 3 4 5

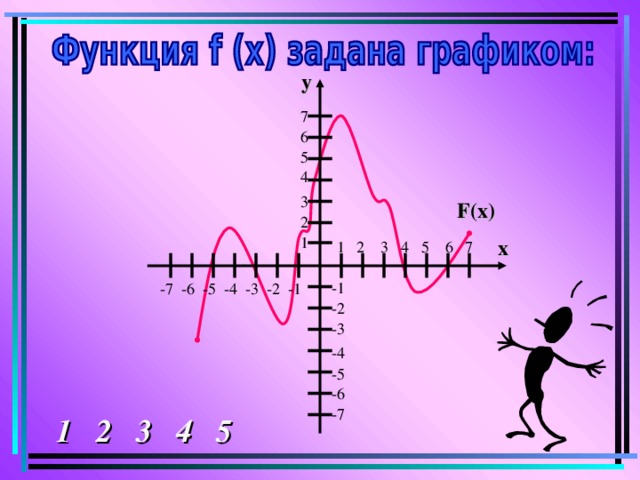
а) Укажите область определения функции.

[-6 ; 7 ]

б ) Укажите область значения функции.

[-4 ; 7]

в) Определите четность функции.

  Не является четной и нечетной функцией.

г) Укажите нули функции.

-5; -3; -1; 4; 6

д) Укажите промежутки возрастания и

убывания функции.

Функция возрастает на отрезках:

[-6; -4], [-2; 1] и [4,5; 7].

Функция убывает на отрезках:

[-4; -2] и [1; 4,5].

Тест № 1. Область определения функции

1) Функция задана графиком.

Укажите область определения этой

функции.

2) Функция задана графиком.

Укажите область определения этой

функции.

1) [-2; 0] 2) [-1; 0]

3) [-1; 3] 4) (-1; 3)

• (-1; 2) 2) [-1; 2)

3) (- ∞ ; 2] 4) [-1; +∞)

3)     Укажите область определения функции.

У = 2х 2 + 7х – 9

1) (0; +∞) 2) [-9; +∞) 3) (-∞; 0) 4) (-∞; +∞)

4)      Укажите область определения функции.

У =√6х-12

1) (2; +∞) 2) (-∞; +∞) 3) [ 2; +∞) 4) (0; +∞)

5) Укажите область определения функции.

У= log 3

1) (-∞; 2) U (4; +∞) 2) (0; 4) 3) (0,5; 4) 4) (-4; 2)

6)     Укажите область определения функции.

У =√5 3х+1 -1

1) (-∞; -1 / 3 ] 2) [ -1/3; +∞) 3) [ 1/3; +∞) 4) ( - ∞; 1/3)

Тест № 2. Область значения функции.

1) Функция задана графиком.

Укажите область значения

этой функции.

2) Функция задана графиком.

Укажите область значения

этой функции.

1)(-3;3) 2) ( -∞;3]

3) [-3;3] 4) (- ∞ ;+ ∞ )

1)( -3;4 ) 2)(- ∞;-3]

3)(-∞;+∞) 4)[-3;4]

3) Укажите область значений функции

у = х 2 + 3х - 2

1) [-2;+ ∞) 2) (-∞; +∞) 3) (-∞; 1) 4) [ 0; + ∞)

4) Укажите область значений функций

у = 4 – 5х – х 2

1) (4; + ∞) 2) (-∞; 4 ] 3) (-∞; +∞) 4) (0; +∞)

5) Укажите область значений функции

у = 4 – cos х

1) [-1; 1] 2) [-5; -3] 3) [3; 5 ] 4) (- ∞; +∞)

6) Укажите область значения функции

у = | x - 1 |

1) (- ∞; +∞) 2) (1;+∞) 3)(- ∞ ; 1) 4)[0; + ∞ )

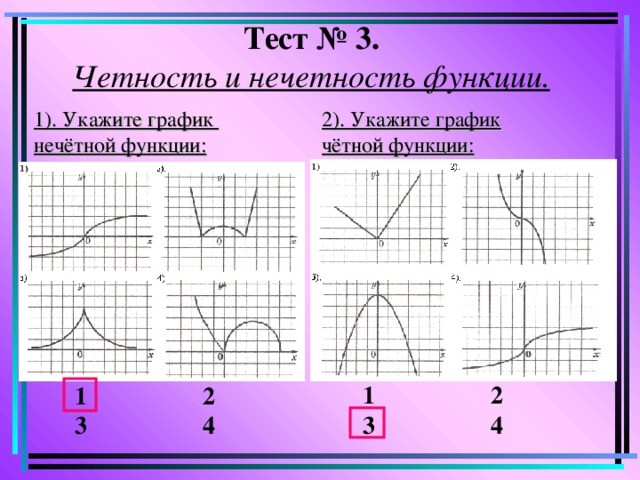
Тест № 3 . Четность и нечетность функции.

1). Укажите график

нечётной функции:

2 ). Укажите график

чётной функции:

1 2

3 4

1 2

3 4

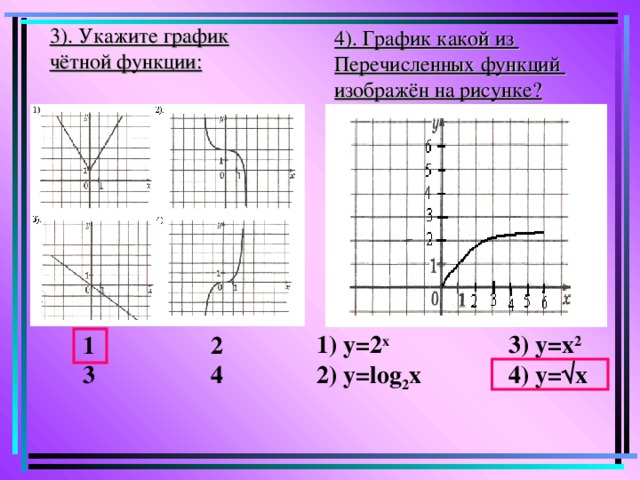
3). Укажите график

чётной функции:

4). График какой из

Перечисленных функций

изображён на рисунке?

1) у=2 х 3) y = x 2

2) у= log 2 x 4) y = √х

1 2

3 4

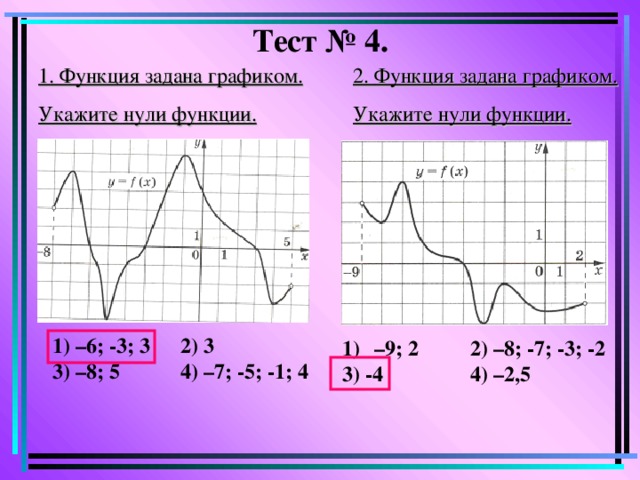
Тест № 4 .

1. Функция задана графиком.

Укажите нули функции.

2. Функция задана графиком.

Укажите нули функции.

1) –6; -3; 3 2) 3

3) –8; 5 4) –7; -5; -1; 4

• – 9; 2 2) –8; -7; -3; -2

3) -4 4) –2,5

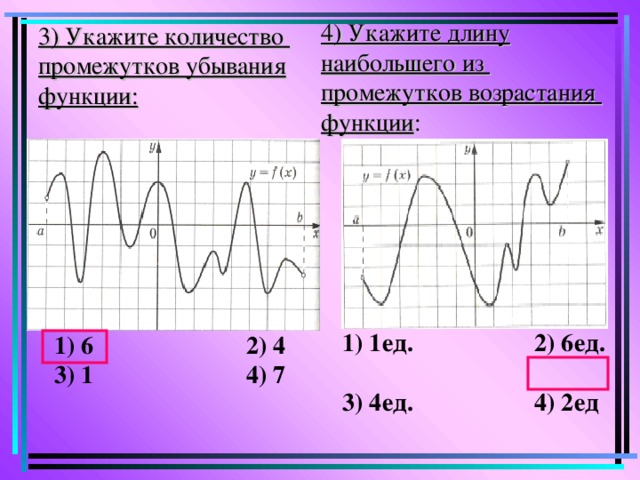
4) Укажите длину наибольшего из

промежутков возрастания

функции :

3) Укажите ко личество

промежутков убывания

функции:

1) 1ед. 2) 6ед.

3) 4ед. 4) 2ед

1) 6 2) 4

3) 1 4) 7

Найдите производную функции

у = 6х 3 + х 6 .

1) у ' = 6х 2 + х 5 2) у ' = 18х 2 + 6 х 5

3) у ' = 18х+ 6х 5 4) у ' = 6х 2 + 6 х

Найдите производную функции

у = х 2 +х 3 + 7 х –4.

1) у ' = х+3х 2 + 7х -4 2) у ' = 2х+х 2 +7

3) у ' = 2х+3х 2 + 7 4) у ' = 2х + 3х 2 - 4

0 в каждой точке интервала I , то функция f возрастает на I . Достаточный признак убывания функции . Если f ' ( х) 0 в каждой точке интервала I, то функция f убывает на I" width="640"

Тема урока: Признак возрастания и убывания функции .

Достаточный признак

возрастания функции.

Если f ' (x) 0 в каждой точке интервала I , то функция f возрастает на I .

Достаточный признак

убывания функции .

Если f ' ( х) 0 в каждой точке интервала I, то функция f

убывает на I

• Пример: стр. 146 № 281 ( а)

• Найдите промежутки возрастания

и убывания функции:

f( х) = 12х + 3х 2 – 2х 3

Дома:

Стр. 143-145, разобрать

теоретический материал,

№ 279 (в,г),

№ 280 (в,г),

№ 281 (в,г).

Функция у = f (x) определена на промежутке

(-5;7).График ее производной изображен на рисунке. Найдите количество промежутков возрастания функции f (x) . В ответе укажите наибольшую из длин этих промежутков.

Ответ: У этой

функции 2

промежутка

возрастания:

[ -3; 2 ] и [ 6; 7 ] .

А наибольшая

длина – 5 ед .

Спасибо за внимание.

Урок окончен.