Векторлардың скалярлық көбейтіндісі .
Білімділік: Векторлық скалярлық көбейтіндісінің анықтамасы, теңдігін, векторлардың скалярлық көбейтіндісінің геометриялық мағынасын, векторлардың перпендикулярлық белгісін білу; координаторлары берілген векторлардың скалярлық көбейтіндісін, векторлар арасындағы бұрыштың шамасын таба алу, скалярлық көбейтінді туралы теореманы дәлелдей алу.Дамытушылық: Өтілген тақырып бойынша алған білімдерін есеп шығрағанда қолдана білу қабілеттерін дамыту.Тәрбиелік: өз бетімен жұмыс істей білуге, шапшаңдыққа, тапқырлыққа тәрбилеу.
Просмотр содержимого документа
«Векторлардың скалярлық көбейтіндісі.»
Тақырып: Векторлардың скалярлық көбейтіндісі . 2 сағат.
Білімділік: Векторлық скалярлық көбейтіндісінің анықтамасы,
Дамытушылық: Өтілген тақырып бойынша алған білімдерін есеп шығрағанда қолдана білу қабілеттерін дамыту.
Тәрбиелік: өз бетімен жұмыс істей білуге, шапшаңдыққа, тапқырлыққа тәрбилеу.
Мақсат: Оқулықтағы жаттығуларды орындай алу мақсаты көзделеді.
Құрал-жабдықтар,көрнекті құралдар: сызғыш, сызба плакаттар.
Сабақ түрі: жаңа білім алу сабағы.
Әдіс-тәсілдер: Лекция.
Сабақ барысы
Оқыту үрдісінің маңыздылығы:
1.Ұйымдастыру кезеңі.
2.Үй жұмысын тексеру.
Үйге берліген тапсырманы тақтаға жазғызып талқылау (оқушылар үйден шығара алмаған есептерді)
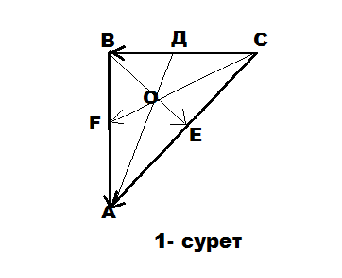
ДМ.(С тобы) АВС үшбұрышының АД, ВЕ, СҒ медианалары О нүктесінде қиылысады.
Шешуі:
Жаңа тапсырмаларды қалыптастыру:
I. Анықтама.
Яғни, , ( 1) мұндағы
(2)
О
Қасиеттері:
Дәлелдеуі:
ә) Егер
II .
.
III. Теорема: Екі вектордың скалярлық көбейтіндісі олардың сәйкес координаторларының көбейтіндісінің қосындысына тең.
Дәлелдеуі.
*(
(3)
Дербес жағдай:
(4)
Жаңа білімді бекіту: Есептер шығару
№1 Үшбұрыштың А(1;1), В(4;1), С(4;5) төбелері берілген, үшбұрыш бұрыштарының косинусын есептеңдер. (Шәкілікова. Геометрия 9-сынып. №70)
Шешуі: 1.
0 1 4
2.
;
Жауабы: 0;
№2. (Шыныбеков. Геометрия 9-сынып . №121)
Егер
Шешуі:
(
(
Жауабы:
№3. (Шәкілікова. Геометрия 9- сынып №84)
Жауабы.-2. .
Қосымша есептер: №116; №117 (Шыныбеков. 9- сынып)
№116. Егер
№117 . Егер
0
Үйге тапсырма беру: №69, №72, №81. (Шәкілікова. 9- сынып) . 7- жұмыс, 3,4-нұсқа (ДМ). №123. (Шыныбеков).
Өздік жұмысын алу: (ДМ. 7- жұмыс. 1,2 – нұсқа)
Оқушыларды бағалау : жетістіктері мен кемшіліктерін атап айту.
Сабақты қорытындылау: Өтілген тақырыптың негізгі түйінін сұрау.
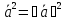 теңдігін, векторлардың скалярлық көбейтіндісінің геометриялық мағынасын, векторлардың перпендикулярлық белгісін білу; координаторлары берілген векторлардың скалярлық көбейтіндісін, векторлар арасындағы бұрыштың шамасын таба алу, скалярлық көбейтінді туралы теореманы дәлелдей алу.
теңдігін, векторлардың скалярлық көбейтіндісінің геометриялық мағынасын, векторлардың перпендикулярлық белгісін білу; координаторлары берілген векторлардың скалярлық көбейтіндісін, векторлар арасындағы бұрыштың шамасын таба алу, скалярлық көбейтінді туралы теореманы дәлелдей алу.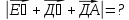 Мұндағы СА
Мұндағы СА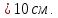
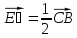 , :
, : 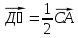 ,
, 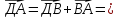
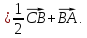
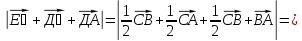
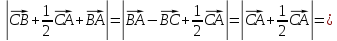
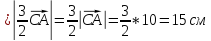
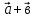 векторларының скалярлық көбейтіндісі деп осы векторлардың ұзындықтарын олардың арасындағы бұрыштың косинусына көбейткендегі көбейтіндіні айтады. Екі вектордың скалярлық көбейтіндісінің белгіленуі:
векторларының скалярлық көбейтіндісі деп осы векторлардың ұзындықтарын олардың арасындағы бұрыштың косинусына көбейткендегі көбейтіндіні айтады. Екі вектордың скалярлық көбейтіндісінің белгіленуі: 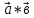 .
.
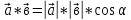 , ( 1) мұндағы
, ( 1) мұндағы 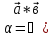 ). 2 сурет
). 2 сурет

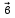
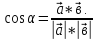 (2)
(2) А
А .
. 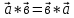 (орын ауыстырымдылық)
(орын ауыстырымдылық)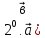 +
+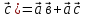 (үлестірімділік заңы)
(үлестірімділік заңы)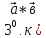 )
)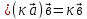 (
( (көбейтіндінің үлестірімділік қасиеті)
(көбейтіндінің үлестірімділік қасиеті)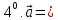 0, онда
0, онда 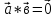
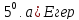
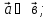 онда
онда 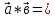 0
0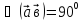 , яғни
, яғни 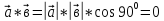
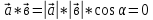 , (
, (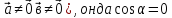 , бұдан
, бұдан 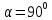 ;
; 
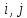 координаталық вектор.
координаталық вектор. 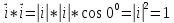
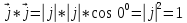 .
.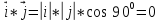
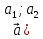 ),
), 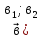 ),
), 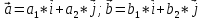
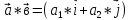 *(
*(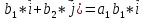 *
*















