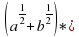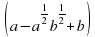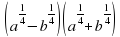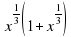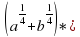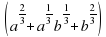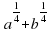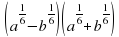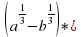Урок позволит показать, как учащиеся усвоили изученный материал и как они умеют применять полученные знания при решении конкретных задач.
Цели урока:
Научить выполнять простейшие преобразования выражений, содержащие степени с дробным показателем;
Закрепить свойства степени с рациональным показателем в ходе выполнения упражнений;
Формировать навыки самоконтроля учащихся;
Создать атмосферу заинтересованности каждого ученика в работе, развивать познавательную активность учащихся;
Воспитывать интерес к предмету, к истории математики.
Оборудование:
карточки с ответами для устного счёта;
карточки с заданиями, дешифраторами для каждого учащегося;
мультимедиа;
презентация Microsoft Excel.
Результативность:
Оттачивается навык применения свойств степени с рациональным показателем при вычислении выражений;
Развиваются вычислительные навыки, повышается вычислительная культура;
Через связь заданий урока с историческими фактами повышается интерес к их выполнению;
Выявляется степень освоенности материала.
Ход урока
I. Организационный момент.
Учитель. Мы заканчиваем изучение темы “Степень с рациональным показателем и её свойства”. Ваша задача на этом уроке, показать, как вы усвоили изученный материал и как вы умеете применять полученные знания при решении конкретных задач.
Актуализация знаний учащихся.
Учитель. Для начала вспомним свойства степеней с рациональным показателем на конкретных примерах.
Задание: представить в виде степени с рациональным показателем.
а) x^(2/5)?x^(1/2) г) (a?a^0,5 )^2 ж) y^(1/2)?√(1/y)
б) x^0,5: x^(1/3) д) (?(x^3 ))2 з) (1/a^2,5 ) -2
в) (y^(5/7))1,4 е) x^(1/9)??(x^2 ) и) √(?(y^4.))
III. Закрепление изученного материала.
Учитель. Один великий русский ученый в свое время сказал: "Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь". Кому принадлежат эти слова, мы узнаем, когда выполним следующие задания.
9^(1/2) –
?64?^(1/3) –
4^(0,5) –
(2^(2/5) )^5 –
50√0,04 –
6^(3/2)/6^0,5 -2 –
?0,7?^(1/2)??70?^(1/2) –
?16?^(1/5)??64?^(1/5) –
?25?^(-1/2) –
4 7 2 –3 3 100 0,2 10
о с м а л е в н
ЛОМОНОСОВ
Михаил Васильевич Ломоносов своим высказыванием указал на важность степеней для науки и человечества.
Учитель. Понятие степени с натуральным показателем сформировалось ещё у древних народов.
Задание. Упростив и вычислив следующие выражения, используя дешифратор, вы узнаете имя ученого, который положил начало буквенных записей степени.
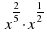 г)
г)  ж)
ж) 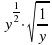
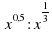 д) (
д) (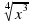 )2 з) (
)2 з) ( ) -2
) -2 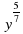 )1,4 е)
)1,4 е) 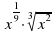 и)
и) 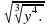
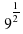 –
– 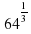 –
– 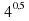 –
– 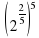 –
–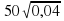 –
–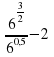 –
– 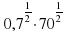 –
–  –
– 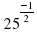 –
–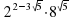 –
–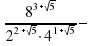
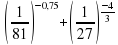 –
–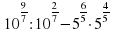 –
–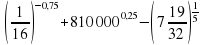 –
– –
–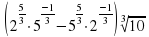 –
–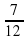
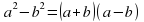

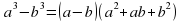
 –
– –
–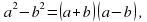 разложить на множители:
разложить на множители: –
–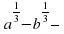
 –
–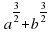 –
–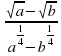 –
–