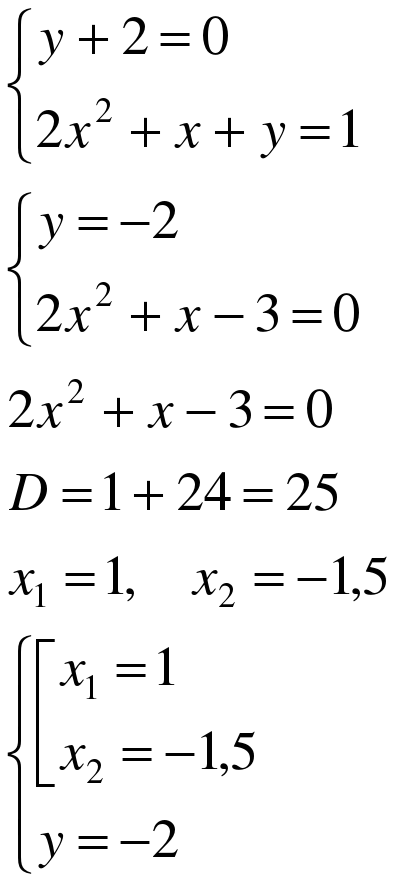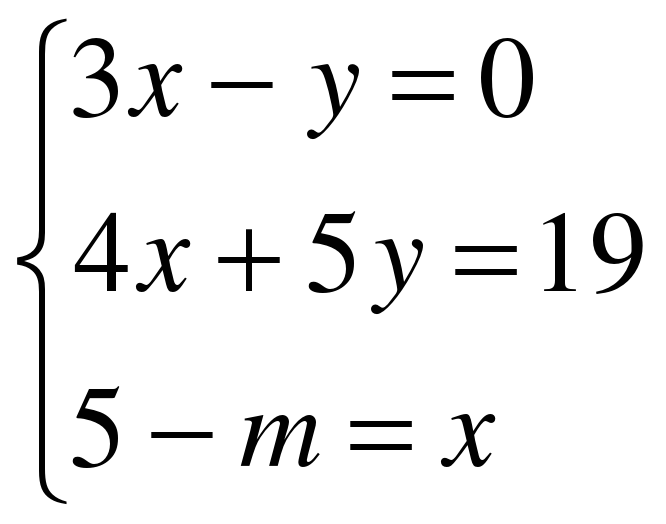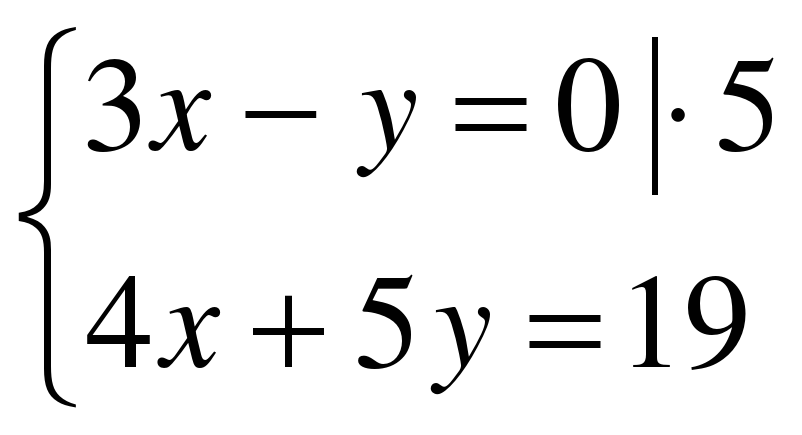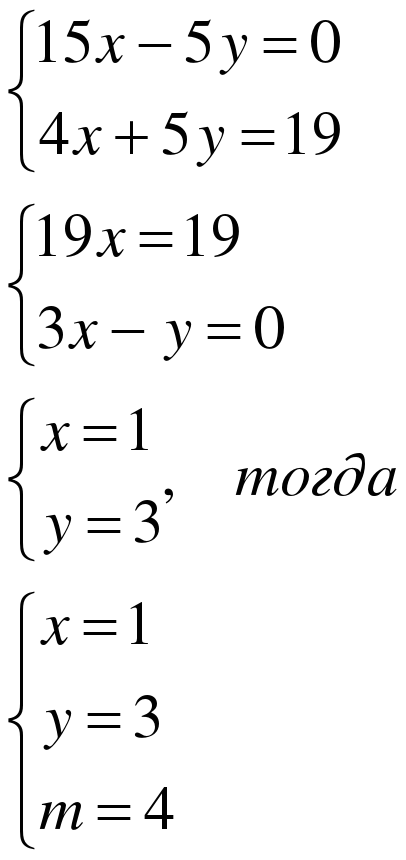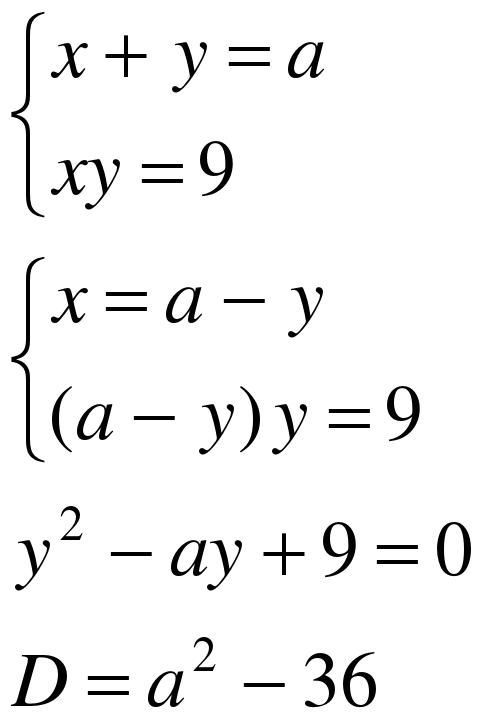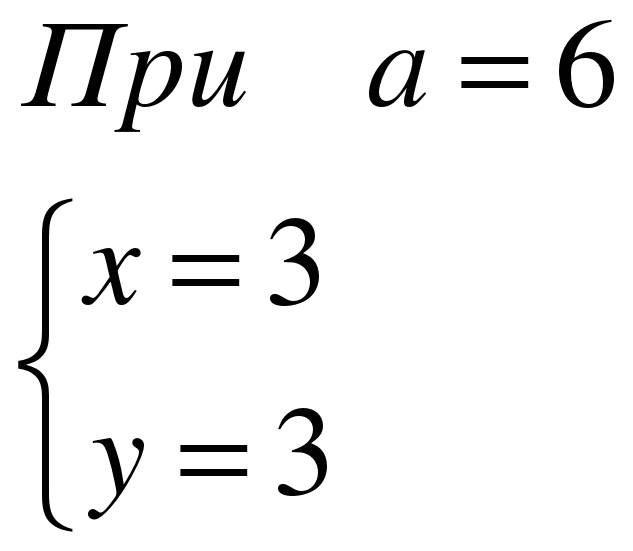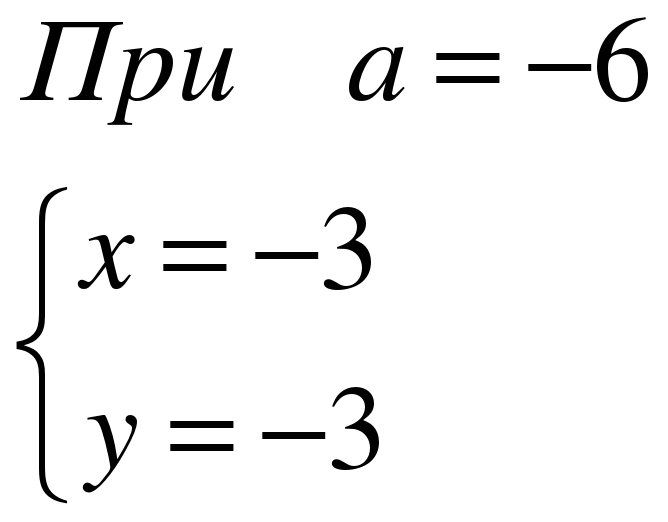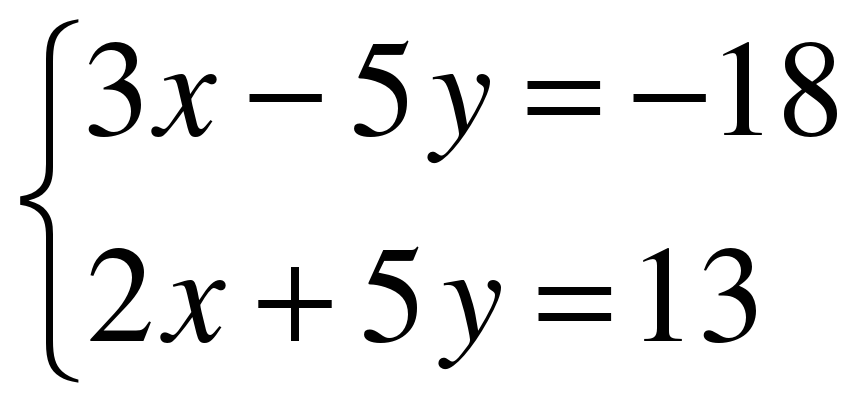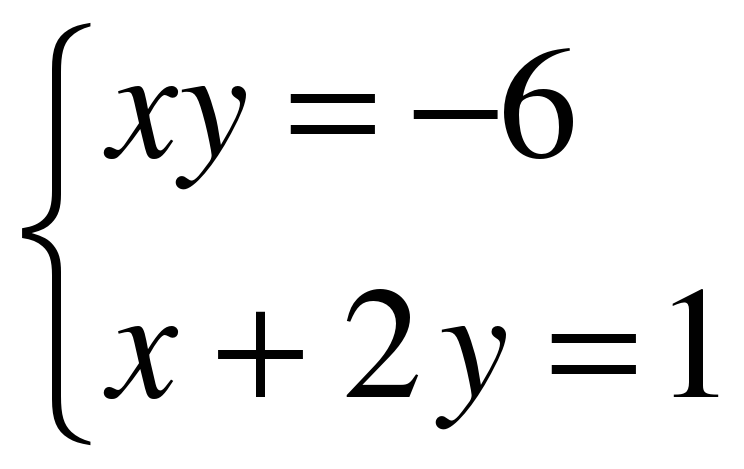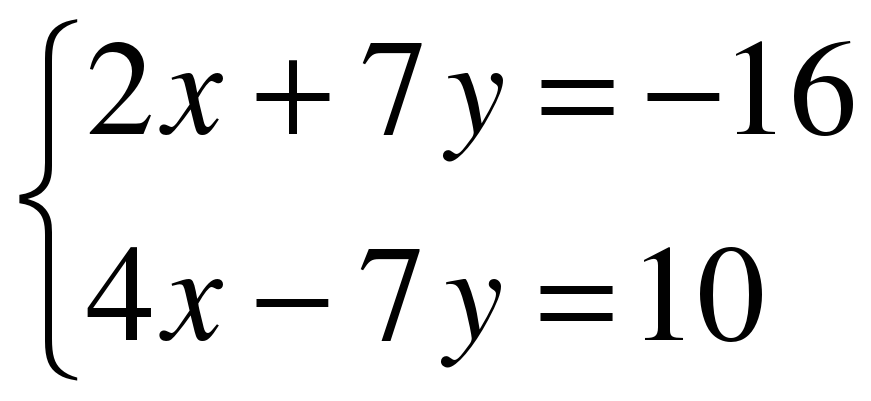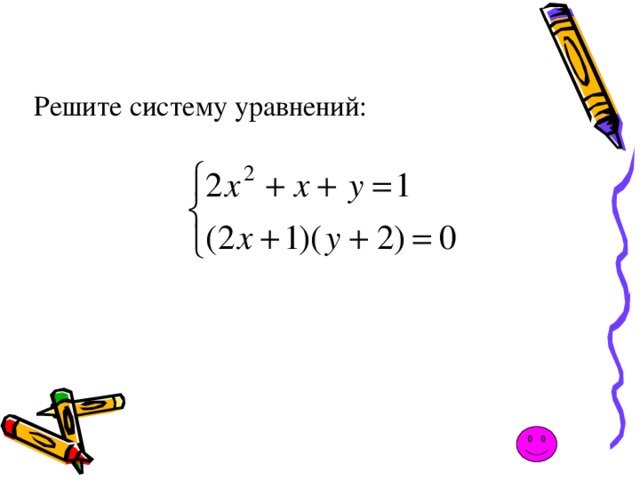Тест
Групповая работа
Самостоятельное решение системы
Система уравнений с параметром
Самостоятельная работа
Домашнее задание
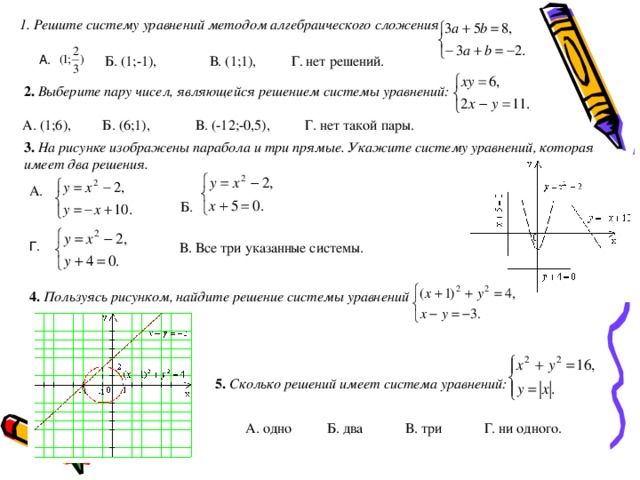
1. Решите систему уравнений методом алгебраического сложения
А.
Б. (1;-1), В. (1;1), Г. нет решений.
2. Выберите пару чисел, являющейся решением системы уравнений:
А. (1;6), Б. (6;1), В. (-12;-0,5), Г. нет такой пары.
3. На рисунке изображены парабола и три прямые. Укажите систему уравнений, которая
имеет два решения.
Б.
А.
Г.
В. Все три указанные системы.
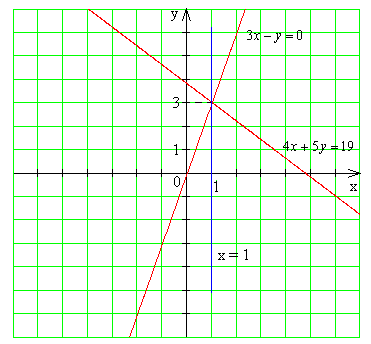
4. Пользуясь рисунком, найдите решение системы уравнений
5. Сколько решений имеет система уравнений:
А. одно Б. два В. три Г. ни одного.
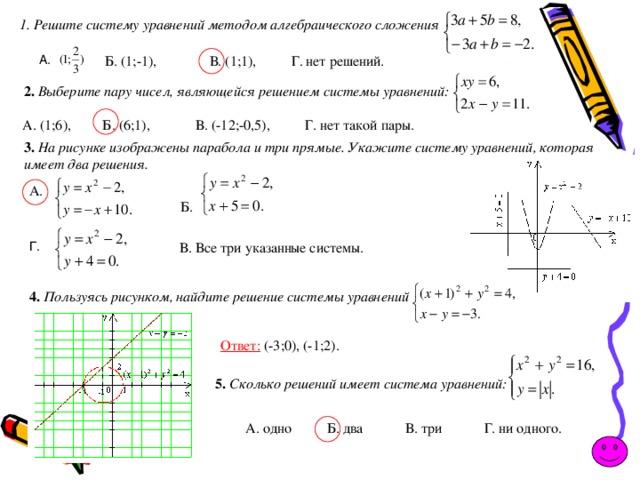
1. Решите систему уравнений методом алгебраического сложения
А.
Б. (1;-1), В. (1;1), Г. нет решений.
2. Выберите пару чисел, являющейся решением системы уравнений:
А. (1;6), Б. (6;1), В. (-12;-0,5), Г. нет такой пары.
3. На рисунке изображены парабола и три прямые. Укажите систему уравнений, которая
имеет два решения.
Б.
А.
Г.
В. Все три указанные системы.
4. Пользуясь рисунком, найдите решение системы уравнений
Ответ: (-3;0), (-1;2).
5. Сколько решений имеет система уравнений:
А. одно Б. два В. три Г. ни одного.

Решите систему уравнений
1 группа – графическим методом
2 группа – методом алгебраического сложения
3 группа – методом подстановки

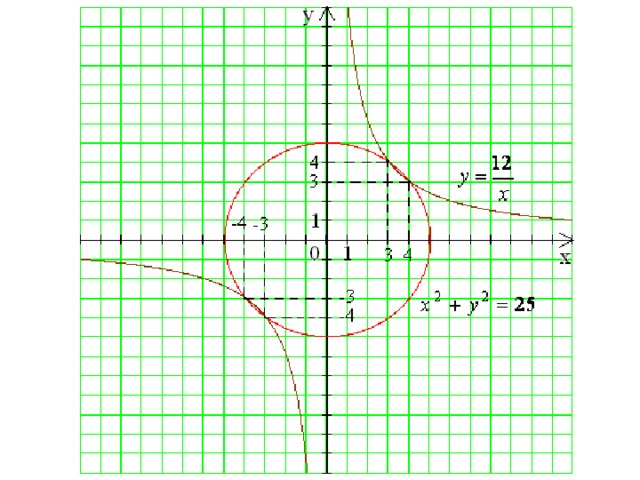
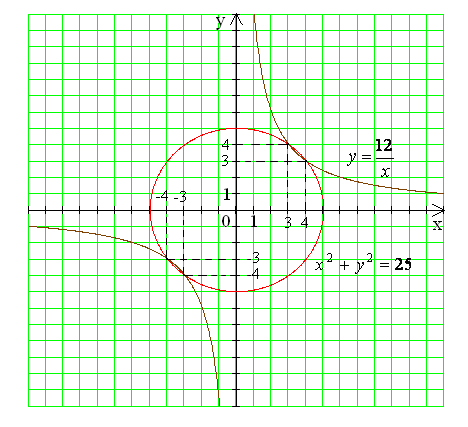
Графический метод.
- окружность с центром в начале координат и радиусом 5.
- обратная пропорциональность, графиком является гипербола,
ветви которой расположены в 1 и 3 координатной четверти.
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).

Метод алгебраического сложения
или
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).

Метод подстановки
Вернемся к y :
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).
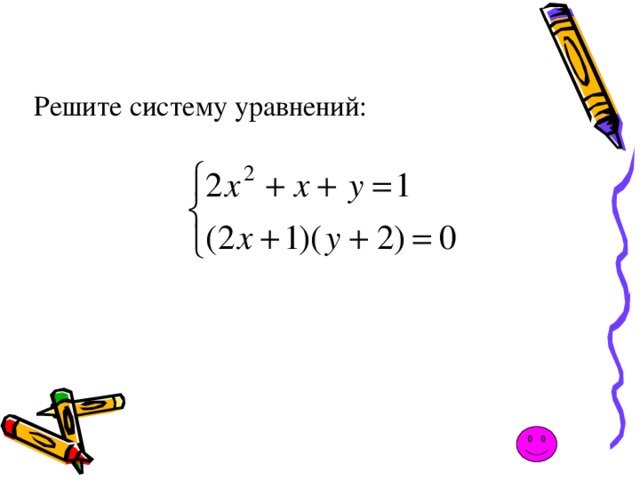
Решите систему уравнений:

При каких значениях m имеет решение
система уравнений
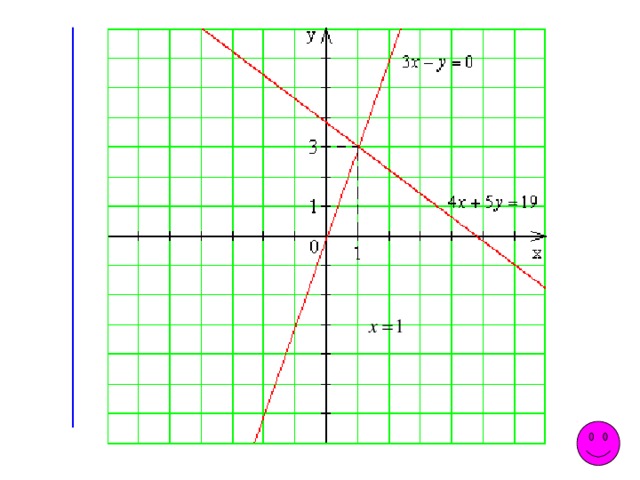

При каком значении параметра а система
уравнений имеет единственное решение.
Найдите это решение.
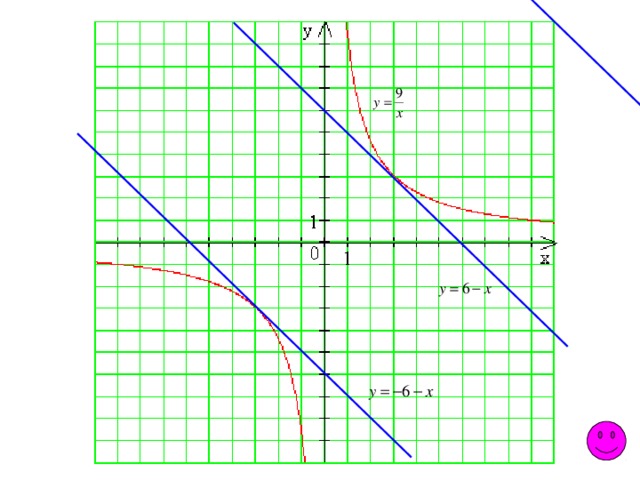

Самостоятельная работа
На «3»
I ВАРИАНТ
II ВАРИАНТ
Решите систему уравнений
Решите систему уравнений
1)
1)
2)
2)
На «4» и «5». Выберите 2 понравившиеся вам системы .
II ВАРИАНТ
I ВАРИАНТ
1) Решите систему уравнений
1) Решите систему уравнений
а)
б)
б)
а)
2) При каких значениях b система имеет
одно решение?
2) При каких значениях b система имеет
одно решение?

Домашнее задание
Уровень А
Уровень Б
Решите системы уравнений
Задача – шутка:
В теплом хлеве у бабуси
Жили кролики и гуси.
Бабка странною была
Счет животным так вела:
Выйдет утром за порог
Сосчитает – 300 ног
А потом без лишних слов
Насчитает 100 голов.
И со спокойною душой
Идет снова на покой
Кто ответит поскорей
Сколько было там гусей?
Кто узнает из ребят
Сколько было там крольчат?
а)
а)
б)
б)
в)
в)
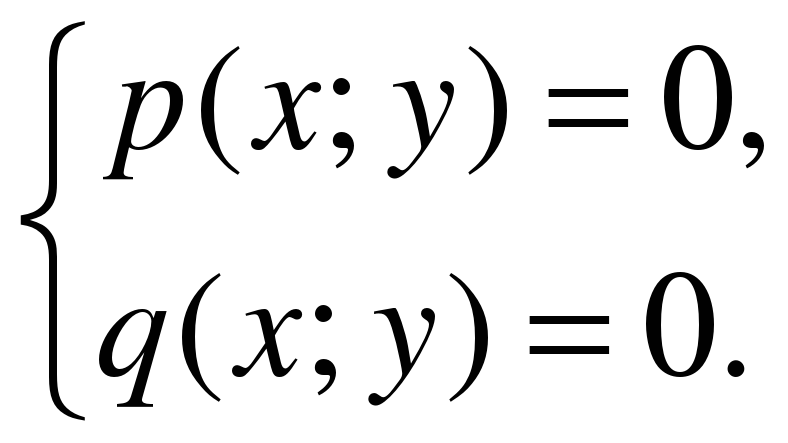 ).
).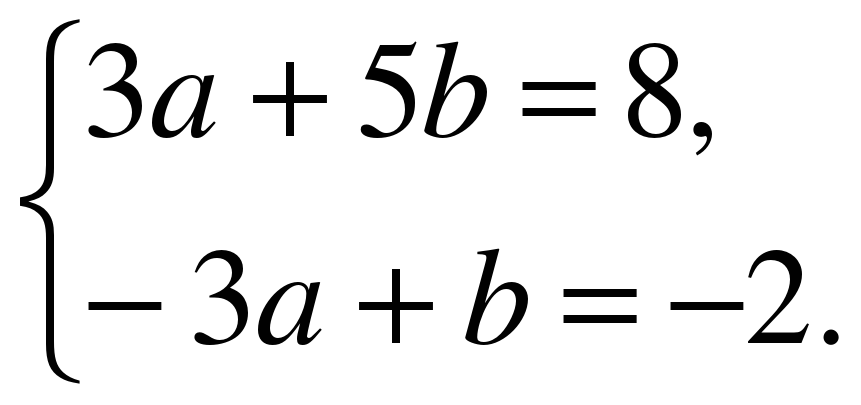
 .
. 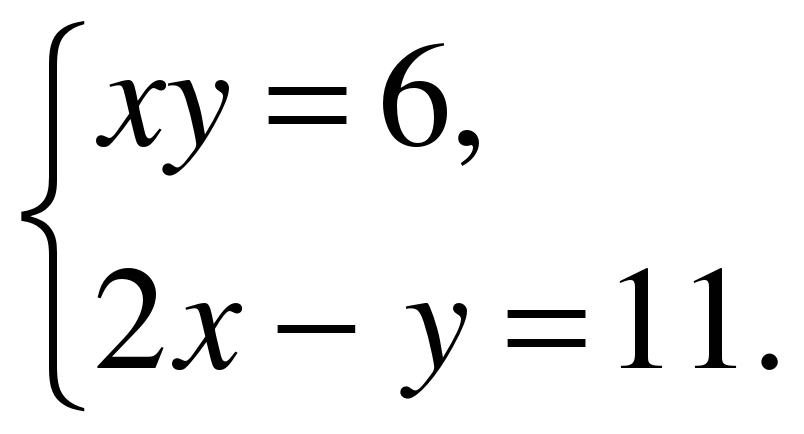
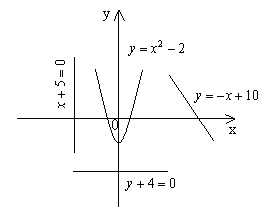
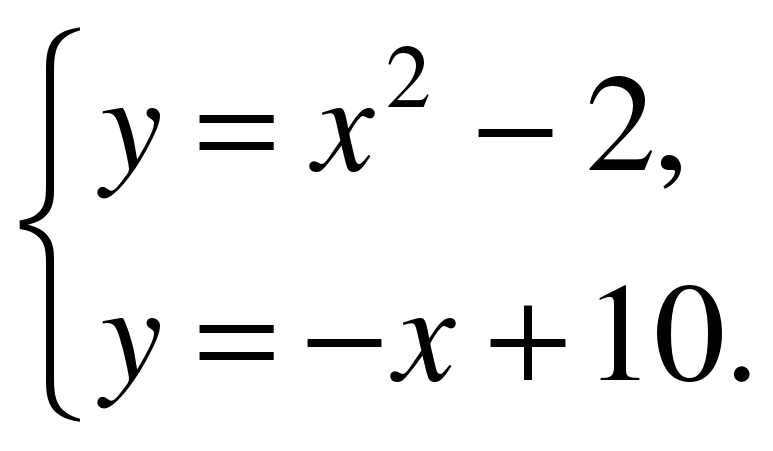 Б.
Б. 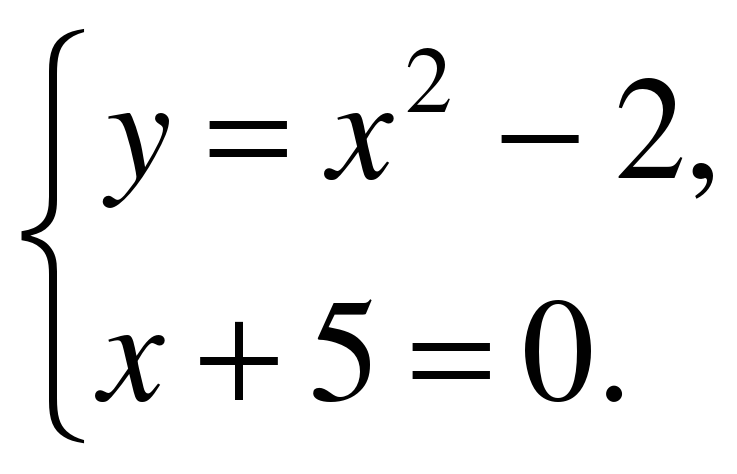
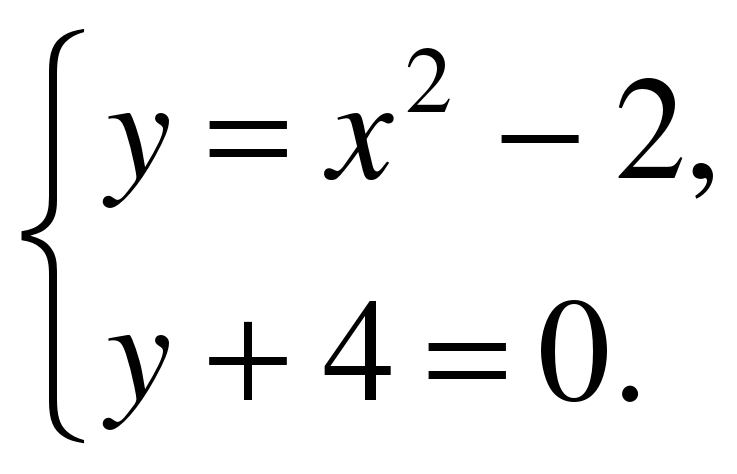 В. Все три указанные системы.
В. Все три указанные системы.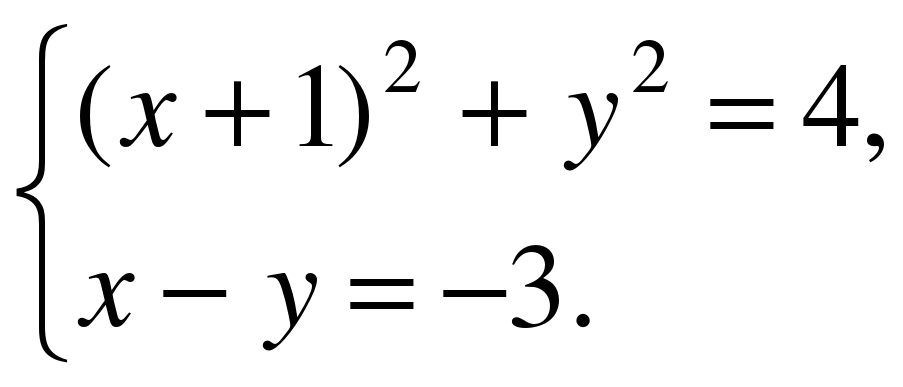
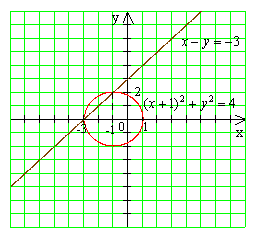 Ответ: (-3;0), (-1;2).
Ответ: (-3;0), (-1;2).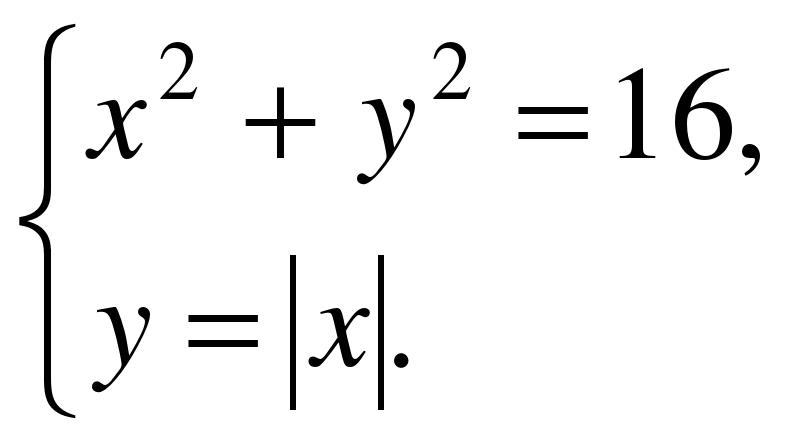
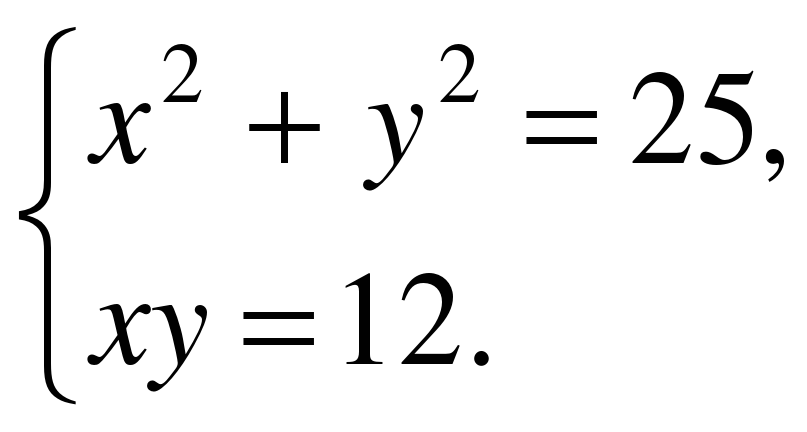
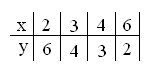
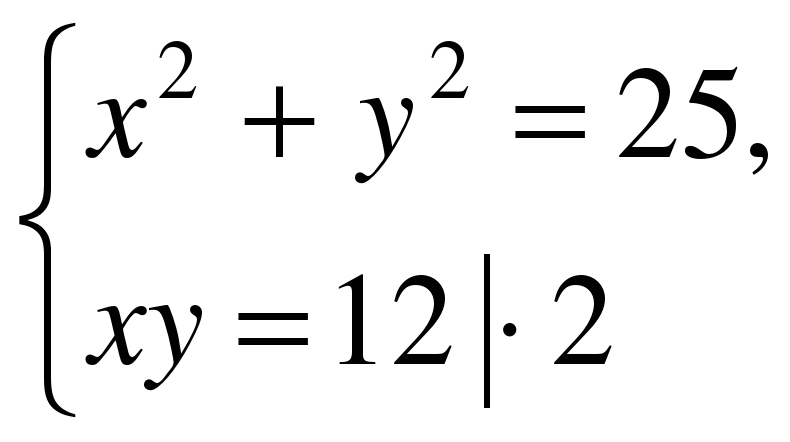
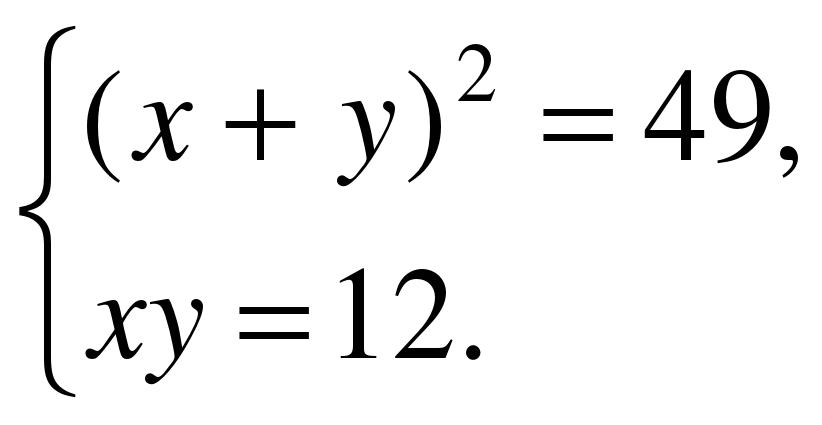
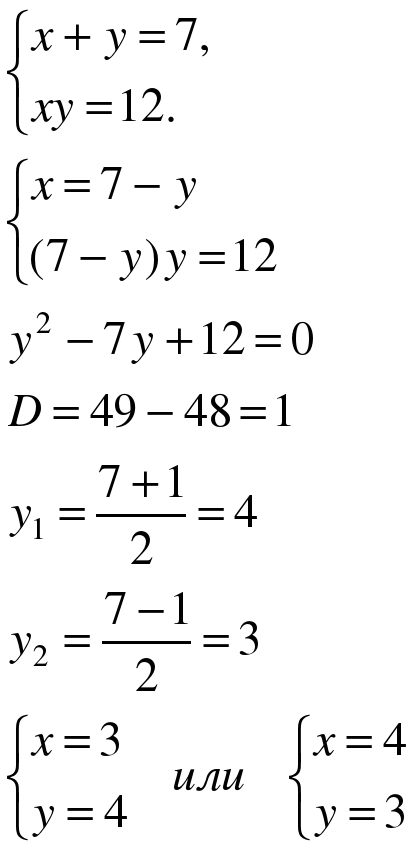 или
или 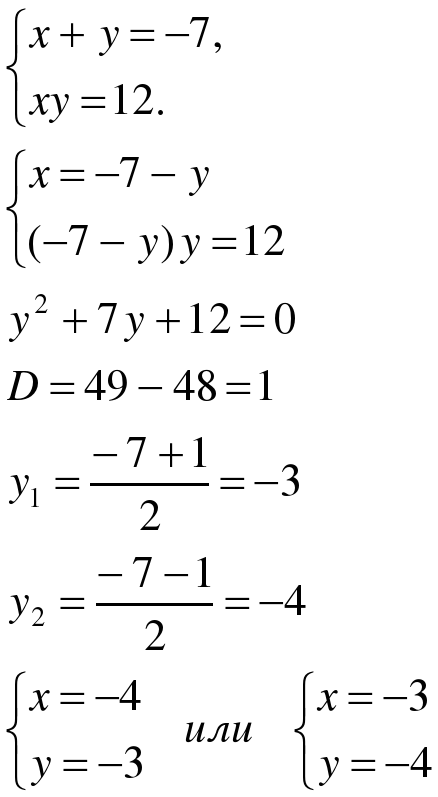
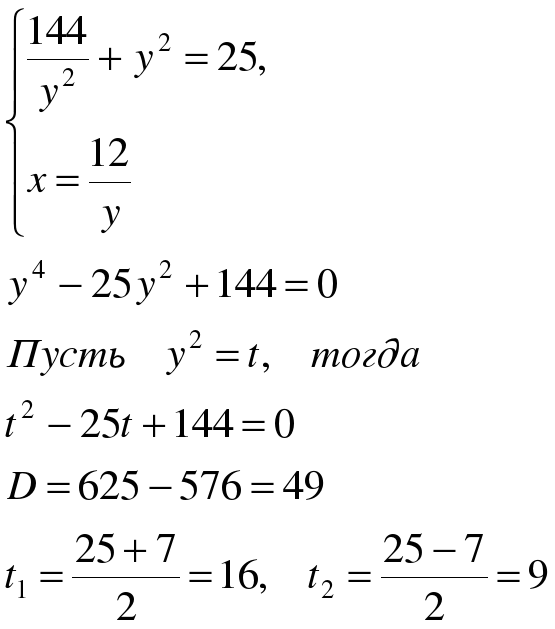
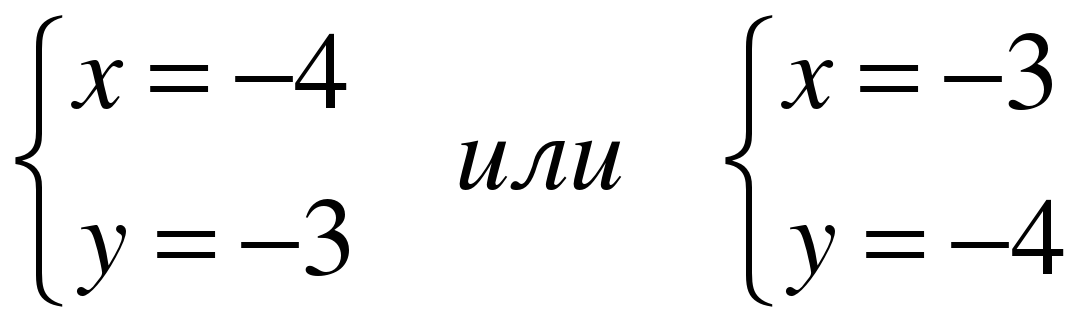
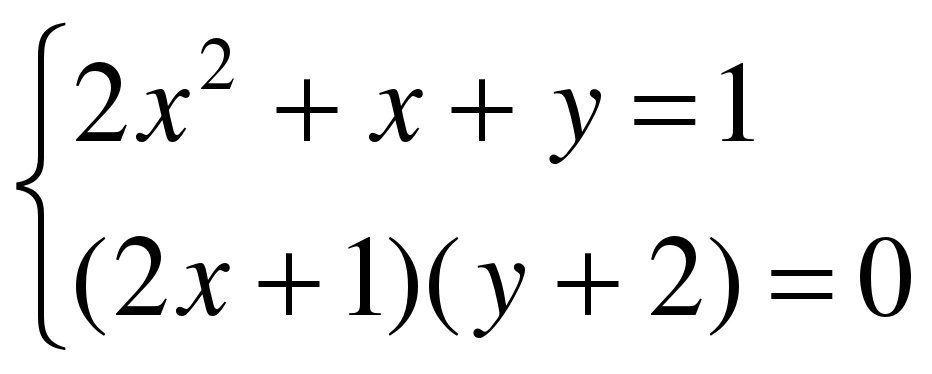
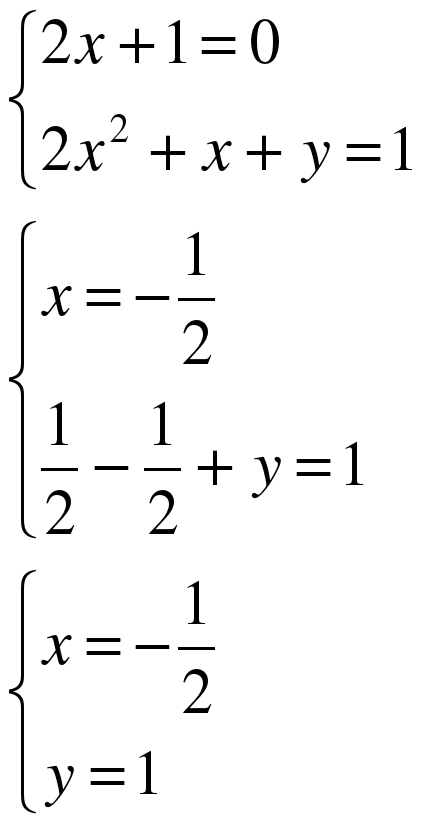 или
или