Данная разработка урока предназначена для итогового повторения в 10 классе по теме "Касательная к графику функции". Также можно использовать материал при подготовке к ЕГЭ в 11 классе. В материале представленны различные типы заданий, взятые из материалов ЕГЭ. Сначала учащимся предлагается теоретическая справка по теме с подробным разбором решений некоторых примеров.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок алгебры и начал анализа в 10 классе "Касательная к графику функции"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок алгебры и начал анализа в 10 классе "Касательная к графику функции"»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2020 руб.
2880 руб.
1670 руб.
2380 руб.
2000 руб.
2860 руб.
2020 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
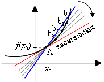
 Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).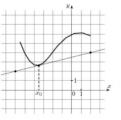

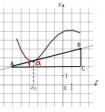

 в точке с абсциссой х0=1.
в точке с абсциссой х0=1. 

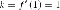

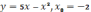

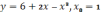

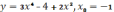
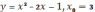
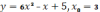
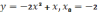

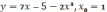

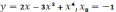
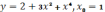
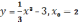
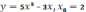


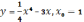
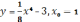

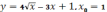


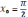
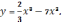

 ,
,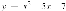
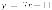 ,
,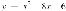
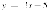 ,
,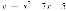
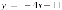 ,
,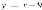 ,
,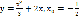 ;
;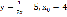 ;
;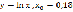 ;
;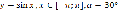 ;
;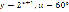 ;
;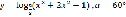 ;
;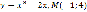 ;
;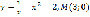 ;
;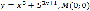 ;
;















