Конспект урока по математике на тему "Уравнение касательной к графику функции"

Краевое государственное бюджетное образовательное учреждение начального профессионального образования

«Профессиональное училище №86».

Методическая разработка учебного занятия

теоретического обучения

ПО МАТЕМАТИКЕ

ТЕМА :  Уравнение касательной

к графику функции

 

Преподаватель: Баскакова

Татьяна Владимировна

Красноярск, 2014

Тема: Уравнение касательной к графику функции

Цели:

• Отработать умения и навыки вычисления производной функции, нахождение производной функции в точке; вырабатывать у обучающихся умения и навыки в составлении уравнения касательной к графику функции в точке;

• развивать внимание, зрительную память, логическое и образное мышление, познавательный интерес, активность учащихся на уроках;

• воспитывать аккуратность, прививать интерес к предмету, воспитывать познавательную активность, самостоятельность.

Тип урока: комбинированный.

Методы организации учебной деятельности:

• беседа;

• частично-поисковый;

• объяснительно-иллюстративный.

Оборудование: учебник «Алгебра и начала анализа 10-11» А.Г. Мордкович, сборник для подготовки к экзамену Дорофеев, компьютер, мультимедиа проектор, программа виртуальной школы Кирилла и Мефодия «Уроки алгебры 10-11», урок с использованием интерактивной доски составлен в программе Notebook 10, памятки для обучающихся, опорный конспект.

Этапы урока.

1. Организационный момент

2. Домино (проверка таблицы производной)

3. Решение упражнений

4. Исторические сведения

5. Вывод формулы уравнения касательной к графику функции. Алгоритм.(использование ЭОР)

6. Закрепление изученного материала из сборника подготовки к экзамену по математике Дорофеев

7. Физ. минутка

8. самостоятельная работа

9. Домашнее задание.

10. Итоги урока. 

Ход урока.

1. Преподаватель :На предыдущих уроках мы с вами находили производные различных функций. Какими формулами мы пользовались?

Обучающиеся: Формулами производной линейной, степенной и постоянной функции

Преподаватель Какие правила необходимо еще знать для нахождения производной функций?

Обучающиеся: Правила дифференцирования.

Преподаватель Сегодня мы применим наши знания и умения для того, чтобы больше узнать о производной и о других интересных фактах из истории математики.

2. Игра «Домино»(Приложение №1)

В комплекте «Домино» 20 карточек. Пары перемешивают свои карточки, делят пополам и начинают раскладывать домино с карточки, в которой заполнена только правая или левая часть. Далее вы должны найти на другой карточке выражение тождественно равное выражению на первой карточке и т. д. В результате получается цепочка.

Домино считается разложенным только тогда, когда все карточки использованы и крайние половинки последней и первой карточки пустые.

Если не все карточки разложены, значит, вы где - то допустили ошибку, и её нужно найти.

Критерии оценки:

• “5” – без ошибок;

• “4” – 1-2 ошибки;

• “3” – 3-4 ошибки.

Составь пару (один из вариантов).

1.	6.	11.	16. а
2. Х	7.	12. - 3	17. cos x
3. 2x	8. sin x	13. - sin x	18.
4. 1	9.	14.	19. 0
5. 2	10.	15. ах	20.

Объяснение задания: В клетках таблицы записаны функции. Для каждой функции найдите производную и запишите соответствие клеток. Например: следовательно ответ:1- 9; и т.д.

Ответы: 1-9; 6-3; 11-14; 16-19; 2-4; 7-18; 12-19; 17-13; 3-5; 8-17; 4-19; 5-19; 15-16;10-20.

3. Решение упражнений

Перед вами опорные конспекты, используя правила производной,

Внимание на экран. Расшифруйте как И. Ньютон назвал производную функции

с	f(x) = 3 x² - 2 x + 4	f '(1) = ?
я	f(x) =x – 4 x³ - 8x+ 13	f '(0) = ?
ю	f(x) = 2x³ - 2 x² + 12 x +7	f '(2) = ?
ф	f(x) =-1,5 х2 -4х+0,125	f '(-1) = ?
и	f(x) = 2 ctgx	f '(-п) = ?
к	f(x) = 2cos x	f '(- п/3) = ?
л	f(x) = tg x +2х	f '( п/4 ) = ?

-1	2	20	√3	4	0	-7

Ответ: ФЛЮКСИЯ

4. Какова история происхождения этого названия? (слайд 14,15)

Понятие производная возникло в связи с необходимостью решения ряда задач физики, механики и математики. Честь открытия основных законов математического анализа принадлежит английскому ученому Ньютону и немецкому математику Лейбницу. Лейбниц рассматривал задачу о проведении касательной к произвольной кривой.

Знаменитый физик Исаак Ньютон, родившейся в английской деревушке Вульстроп, внес немалый вклад и в математику. Решая задачи на проведение касательных к кривым, вычисляя площади криволинейных фигур, он создал общий метод решения таких задач – метод флюксий (производных), а саму производную называл флюентой.

Он вычислил производную и интеграл степенной функции. О дифференциальном и интегральном исчислениях он пишет в своей работе «Метод флюксий» (1665 – 1666гг.), послужившей одним из начал математического анализа, дифференциального и интегрального исчисления, которое ученый разработал независимо от Лейбница.

Многие ученые в разные годы интересовались касательной. Эпизодически понятие касательной встречалось в работах итальянского математика Н.Тартальи (ок. 1500 – 1557гг.) – здесь касательная появилась в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая данность полета снаряда. И. Кепплер рассматривал касательную в ходе решения задачи о наибольшем объеме параллелепипеда, вписанного в шар данного радиуса.

В 17 веке на основе учения Г.Галилея о движении активно развилась кинематическая концепция производной. Различные варианты изложения встречаются у Р.Декарта.

3.Объяснение нового материала (Используется диск Кирилла и Мефодия Уроки Алгебры 10-11 класс, тема 2, урок 5 )

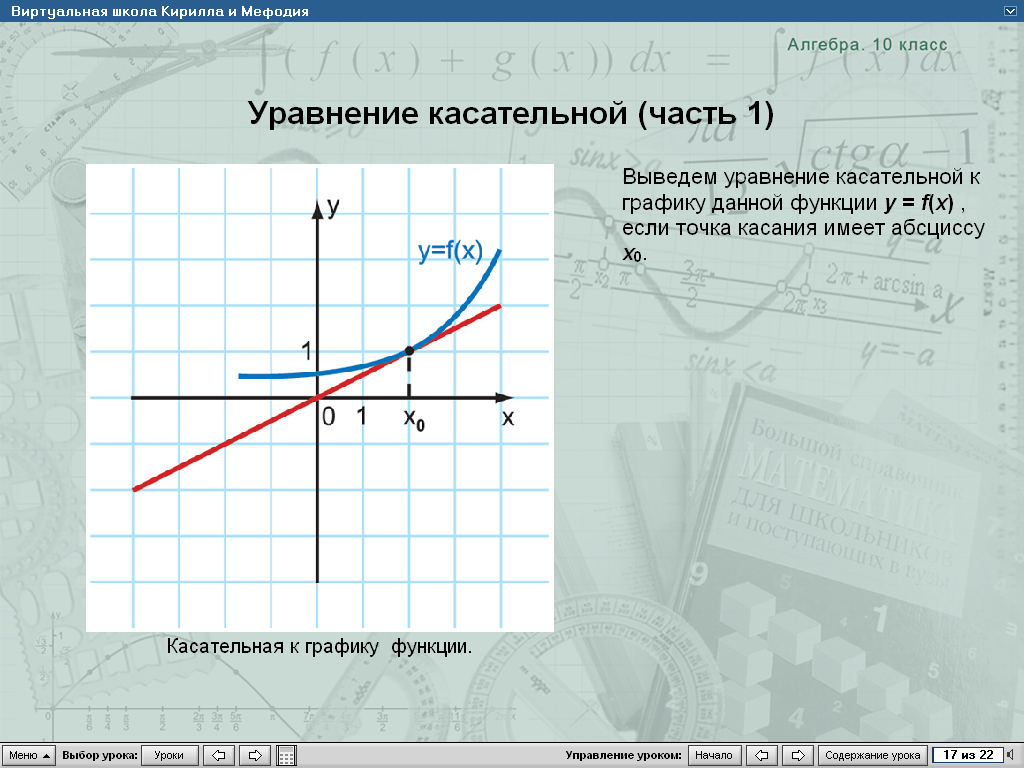
5. Геометрический смысл производной. Уравнение касательной к графику функции. И1

Выведем уравнение касательной к графику функции y = f(x) если точка касания имеет абсциссу х_о

Прежде всего, примем во внимание, что касательная – прямая линия. Если прямая перпендикулярна оси абсцисс, то уравнение прямой имеет вид х=а. Уравнение прямой, не перпендикулярной оси абсцисс в алгебре имеет вид y=kx+b. Нам заранее не известно, будет ли перпендикулярна к оси абсцисс касательная к данному графику в данной его точке. Но мы можем это узнать попытавшись найти значение производной данной функции в данной точке. Если окажется, что производная не существует, то касательная перпендикулярна к оси абсцисс, и ее уравнение х=а. И так как эта касательная проходит через точку с абсциссой х_о, то уравнение касательной выглядит так: х=х_о.

Если же окажется, что производная данной функции в данной точке существует, то уравнение касательной можно привести к виду y=kx+b. Вспомним, что угловой коэффициент прямой k равен тангенсу угла наклона прямой к положительному направлению оси Ох или значению производной функции в точке проведения касательной, т.е. y=f `(х_о)· x+b., т.е уравнение касательной имеет вид:

y = f(xo) + f ´(x_o) · (x – x_o)

с опорного конспекта зарисуйте рисунок и уравнение касательной (приложение1)

Обучающимся выдается памятка для составления алгоритма уравнения касательной

• Найти значение функции в точке х_о

• Вычислить производную функции

• Найти значение производной функции в точке х_о

• Подставить полученные числа в формулу

y = f(x_o) + f `(x_o)( x – x_o)

• Привести уравнение к стандартному виду

6. Закрепим знания на примерах из сборника Дорофеева для подготовки к экзамену №4.165, 4.168 стр.131

7. Физ. минутка

Что кружится, что ложится и на землю, и на крыши,

И о чём поэт зимою по ночам поэмы пишет?

Это первое словечко, а второе просто «на».

Ну а третье? Угадайте, что бежит по проводам?

Напиши, что получилось и прочти наоборот,

Не запутайся, читая слово задом наперёд.

(снег-на-ток….котангенс)

7. ТЕСТ

ВАРИАНТ 1

1. В чём состоит физический смысл производной?

А. Ускорение. Б. Скорость.

В. Угловой коэффициент.

2. Точка движется по прямой по закону S(t) = 2t³ + 3t .

Чему равна скорость точки в момент времени t = 1.

А. 5. Б. 12. В. 9. Г. 3.

3. Заполните пропуски:

а)( )' = 3_ - 4 + _; б) (_ - 25_ - _ )' = ( ).

4. Разбейте на пары «функция - производная».

а) _ ; 1) _

б)_; 2)_;

в) _; 3) _{  }

г)_7_+_ 4)_{ }

5. Найдите угловой коэффициент касательной, проведённой к графику функции f(_) _ через его точку с абсциссой _{ }

А. 8. Б. 4. В. – 8. Г. – 4.

ВАРИАНТ 2

1. В чём состоит геометрический смысл производной?

А. Ускорение. Б. Скорость.

В. Угловой коэффициент.

2. Точка движется по прямой по закону

S(t) = 2t² _. Вычислите ускорение движения.

А. – 4. Б. – 8. В. 4. Г. 8.

3. Заполните пропуски:

а) _' _ ( );

б) ( )' _{  }.

4. Разбейте на пары «функция - производная».

а) _ 1) _

б) _ 2) _

в) _; 3) _{ }

г) _ 4) _

5. Найдите угловой коэффициент касательной, проведённой к графику функции f(_) _через его точку с абсциссой _{ }

А. - 7. Б. 8. В. 7. Г. 9.

Ответ:

Вариант 1 Вариант 2

1. Б; 1. В;

2. В; 2. В;

3. а) _ 3. а) _

б) _ б)_

4. а - 2, 4. а - 3,

б - 4, б - 4,

в - 1, в - 1,

г - 3; г - 2;

5. Б. 5. А.

8.Итог урока

Что нужно знать, чтобы составить уравнение касательной к графику функции? (уметь находить значение функции в точке, касательной к графику функции? Уметь находить значение функции в точке касания)

Домашнее задание: Прототипы Задания ЕГЭ В-9(Приложение№3)

Спасибо за урок!