Методическая разработка по планиметрии
«Свойство биссектрисы треугольника» для обобщения
данной темы при подготовке к ОГЭ и ЕГЭ по математике.
Автор Швец Тамара Александровна,
учитель математики высшей категории
МБОУ СОШ № 65 город Краснодар.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данная работа предназначена для повторения некоторых тем планиметрии, входящих в тематический план изучения геометрии в 10-11 классах по учебнику Атанасяна Л.С. В начале первой четверти учащимся 10 класса необходимо повторить следующие темы: теорема о произведении отрезков хорд; теорема о касательной и секущей, теорема о сумме квадратов сторон и диагоналей параллелограмма; вычисление углов с вершинами внутри и вне круга, угла между касательной и хордой; решение треугольников; вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей; формулы площади треугольника: формула Герона, выражение площади треугольника через радиус вписанной и описанной окружностей. В этой работе рассматривается одна из тем, по которым разработаны такие же учебно-методические материалы, которые содержат в себе теоретические факты с доказательствами, задачи различного уровня сложности с решениями и подборка задач для учащихся с целью более качественного закрепления материала. Их можно также использовать для домашнего задания или контроля знаний. По учебному времени занятие может быть организовано для 1-3 уроков, в зависимости от уровня подготовки учащихся.
- Свойство биссектрисы треугольника
Теорема Биссектриса треугольника делит третью сторону на отрезки,
пропорциональные двум другим сторонам:
- Закрепление учебного материала рассмотрим на примере решение
некоторых задач.
Задача № 1
Стороны треугольника равны 10 см, 11 см и 12 см. Найти отрезки, на которые делит биссектриса треугольника среднюю сторону.
Дано: AC=10 см, BC=11 см, AB=12 см, AP = биссектриса.
Найти: CP и BP.
Решение:
По свойству биссектрисы треугольника:
Пусть CP=x см, тогда BP=11-x см:
откуда по основному свойству пропорции
CP=5 см, BP=6 см.
Ответ: 5 см, 6 см.
Задача № 2
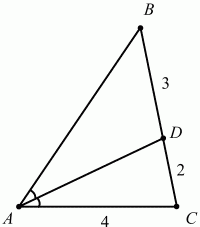
В треугольнике ABC проведена биссектриса AD. Найдите периметр треугольника ABC,
если АС = 4; DC = 2; BD = 3.
По свойству биссектрисы BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.
Периметр треугольника РАВС = 6 + 5 + 4 = 15.
Ответ: 15.
Задача №3
Дан треугольник ABC, в котором < В = 30°, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D. Определите площадь ABD.
Решение. По свойству биссектрисы AD/DC = AB/BC = 4/6 = 2/3.
Пусть AD = 2х; DC = Зх.
Ответ: 12/5.
На протяжении нескольких лет среди заданий ЕГЭ не раз предлагались планиметрические задачи, которые в случае применения этого свойства решались бы проще. Рассмотрим несколько примеров таких задач.
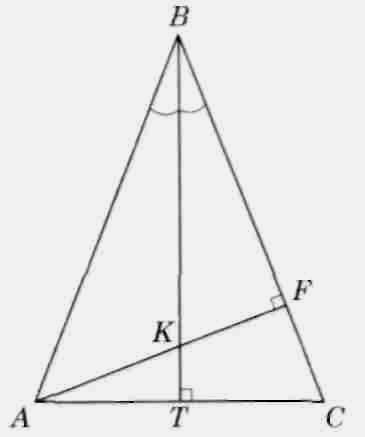
Задача 1. В равнобедренном треугольнике ABC с основанием АС проведены высоты ВТ и AF. Они пересекаются в точке К. Известно, что АВ = 15, АК= 5. Найдите площадь треугольника АВК (рис. 1).
Рис. 1
Решение. Так как высота ВТ, проведенная к основанию равнобедренного треугольника ABC, является биссектрисой угла В, то отрезок ВК - биссектриса угла В треугольника ABF. По свойству биссектрисы треугольника
, откуда .
Пусть KF= х, тогда BF = Зх, AF = = 5 + х. Рассмотрим треугольник ABF. По теореме Пифагора АВ2 = BF2 + AF2, где AF = AK + KF.
Имеем: 225 = (3х)2 + (5 + х)2, х2 + х - 20 = 0, х = 4. Следовательно, BF = 3х = 3 • 4 = 12.
Наконец,
SABК= АK • BF = •5 • 12 = 30.
Ответ: SABК = 30.
Задача 2.
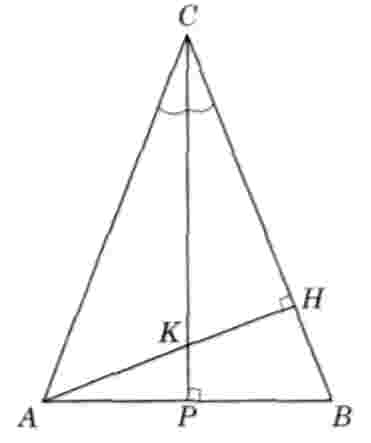
Площадь равнобедренного треугольника ABC равна 90, а боковая сторона равна 10. К основанию АВ и стороне ВС проведены высоты СР и АН соответственно, пересекающиеся в точке К. Найдите площадь треугольника СКН (рис. 2).
Решение. SABC = АС • ВС • sin C,
откуда sin C =, sin C = =
Рассмотрим треугольник АСН. В нем AH = AC • sin C, АН = 10 • = 6. По теореме Пифагора СН2 = АС2 - АН2, откуда СН = 8.
Рис. 2
Так как высота СР, проведенная к основанию равнобедренного треугольника ABC, является биссектрисой угла С, то отрезок СК - биссектриса угла С треугольника АСН. По свойству биссектрисы треугольника
Пусть АК = 5х и КН = 4х. Тогда
9х=6, х=, КН =4• =.
Таким образом,
SCKH= СН•СК= •8 •
Ответ: SCKH = 32.
Задача 3.
Дан ромб ABCD с острым углом В. Площадь ромба равна, а синус угла В равен. Высота СН пересекает диагональ BD в точке К. Найдите длину отрезка СК (рис. 3).
Рис. 3
Решение. Так как диагональ ромба является биссектрисой его угла, то BD - биссектриса угла В, а значит, ВК — биссектриса угла В треугольника НВС. Далее находим сторону и высоту ромба:
ВС = 3, СН = 4 и применяем свойство биссектрисы угла треугольника. Так как
и НК+КС = 4,
то СК =3.
Ответ: СК = 3. Заметим, что учащиеся часто находят площадь треугольника либо как разность площадей двух прямоугольных треугольников, либо по формуле Герона. Рациональнее находить, как показано в решении задач 1 и 2, основание и проведенную к нему высоту.
В данной разработке использованы материалы следующих авторов и сайтов:
- http://www.ankolpakov.ru/tag/zadachnik-po-geometrii/
- http://ege-ok.ru/2015/06/25/svojstva-bissektrisy-mediany-i-vysoty-treugolnika
- Методические материалы: автор Смирнова Марина Николаевна.
- Дидактические материалы к УМК по геометрии авторов И. М. Смирнова,
В. А. Смирнов.
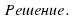 По свойству биссектрисы BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.
По свойству биссектрисы BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.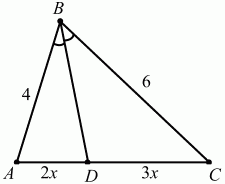
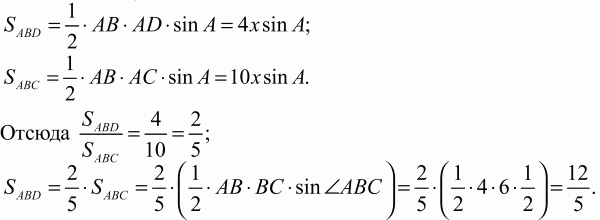
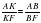 , откуда
, откуда 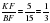 .
. 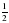 АK • BF =
АK • BF = 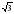 . К основанию АВ и стороне ВС проведены высоты СР и АН соответственно, пересекающиеся в точке К. Найдите площадь треугольника СКН (рис. 2).
. К основанию АВ и стороне ВС проведены высоты СР и АН соответственно, пересекающиеся в точке К. Найдите площадь треугольника СКН (рис. 2).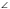 C,
C,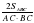 , sin
, sin 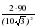 =
=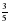
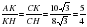
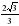 , КН =4•
, КН =4•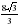 .
.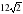 , а синус угла В равен
, а синус угла В равен 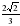 . Высота СН пересекает диагональ BD в точке К. Найдите длину отрезка СК (рис. 3).
. Высота СН пересекает диагональ BD в точке К. Найдите длину отрезка СК (рис. 3).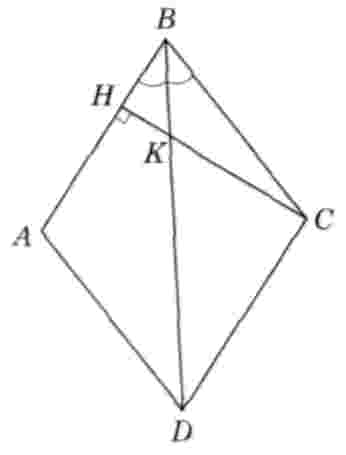
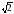 , СН = 4 и применяем свойство биссектрисы угла треугольника. Так как
, СН = 4 и применяем свойство биссектрисы угла треугольника. Так как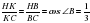 и НК+КС = 4,
и НК+КС = 4,















