Урок геометрии 7 класс " Сумма углов треугольника"

Раздел долгосрочного плана: 7.3.А Взаимное расположение прямых (18 час)

Школа:

Дата:

ФИО учителя:

Класс: 7

Количество присутствующих:

отсутствующих:

Тема урока

Сумма углов треугольника. Внешний угол треугольника

Тип урока

Урок-практикум

Цели обучения

7.1.1.17 применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач;

7.1.1.19 применять теорему о внешнем угле треугольника

Цели урока

Учащиеся применяют теорему о сумме внутренних углов треугольника и следствия из неё при решении задач; применяют теорему о внешнем угле треугольника при решении задач

Критерии оценивания

Уровни мыслительных навыков

Критерии оценивания

Знание, понимание (все учащиеся)

перечисляют элементы треугольника; распознают виды треугольников; находят сумму углов треугольника, внешний угол треугольника

Применение (большинство учащихся)

Применяют знания при решении задач.

Анализ (некоторые учащиеся)

Оценивают значимость данных для решения более сложных задач

Языковые задачи

Лексика и терминология:

Равносторонний треугольник, равнобедренный треугольник, разносторонний треугольник, прямоугольный треугольник, тупоугольный треугольник, остроугольный треугольник, внутренний и внешний угол треугольника

Привитие ценностей

Проявление уважения осуществляется в групповой работе через понимание, умение слушать друг друга. Развитие сотрудничества в групповой и парной работе. Развитие открытости при выполнении самооценивания и взаимооценивания; формирование таких качеств личности, как организованность, дисциплинированность и аккуратность.

Межпредметные связи

Черчение, алгебра

Навыки использования ИКТ

Применение интерактивной доски – презентация

Предыдущие знания

Из курса начальной школы знают фигуру треугольник и умеют находить его периметр; биссектриса; внешний угол; сумма углов треугольника

Ход урока

Запланированные этапы урока

Запланированная деятельность на уроке

Ресурсы

Вызов.

Начало урока

2 минуты

4 минуты

7 минут

7 минут

1 минута

Середина урока

7 минут

15 минут

1. Организационный момент.

Приветствие учеников. Пожелание успеха.

Ознакомление с темой урока, постановка его целей.

Учитель сообщает тему урока, цели урока и согласует их с учащимися. Каждый из учеников должен поставить себе цель на уроке. Например, «Проверить свои знания теории по данной теме и умение решать задачи» (возможны варианты). В течении всего урока учащиеся будут себя оценивать и выставлять свои баллы в лист самоконтроля.

Актуализация знаний учащихся.

1. Проверка домашнего задания.

Ученики на прошлом уроке получили дифференцированное домашнее задание: одна группа составляла кроссворд по теме «Треугольники», вторая заполняла готовый кроссворд по этой же теме, а третья заполняла таблицу «Классификация треугольников» (Нарисовать треугольники в каждой свободной графе таблицы так, чтобы они соответствовали заданным условиям).

Первая и вторая группа сдают домашнее задание, а один из уч-ся третьей группы, выполнивший свое задание демонстрирует его через мультимедийный проектор. Учитель делает обобщение по составленной таблице.

Дескрипторы

• распределяют треугольники в зависимости от углов;

• распределяют треугольники в зависимости от длины сторон;

• называют виды треугольников

• элементы треугольника.

Ф.О.: Оценивание по дескрипторам, в виде устной обратной связи. Учитель делает обобщение по составленной таблице.

Дифференциация: оценивание в виде комментариев

1. Повторение теории

Стратегия «Тонкие и толстые вопросы»

Учащиеся работают в парах. На столе у каждой пары карточка опроса.

Задание: На вопросы 1-3 отвечает 1 вариант, на вопросы 4-6 – второй вариант.

Цель данного задания: проверка знаний теории учащимися. Развитие коммуникативных способностей, умения оценивать друг друга.

1.Чему равна сумма углов треугольника?

2.Дать определение внешнего угла треугольника.

3.Применение теоремы о внешнем угле треугольника.

4.Дать определение остроугольного, прямоугольного и тупоугольного треугольников.

5.Сколько в треугольнике может быть прямых, тупых углов?

6.Почему в тупоугольном треугольнике только один тупой угол?

Дескрипторы:

- называют сумму углов треугольника

- формулируют определение внешнего угла треугольника.

- применяют на практике теорему о внешнем угле треугольника.

- дают определения остроугольного, прямоугольного и тупоугольного треугольников

- применяют теорему о сумме углов треугольника

ФО: взаимопроверка, словесное одобрение учителем и одноклассниками.

Дифференциация по ответам

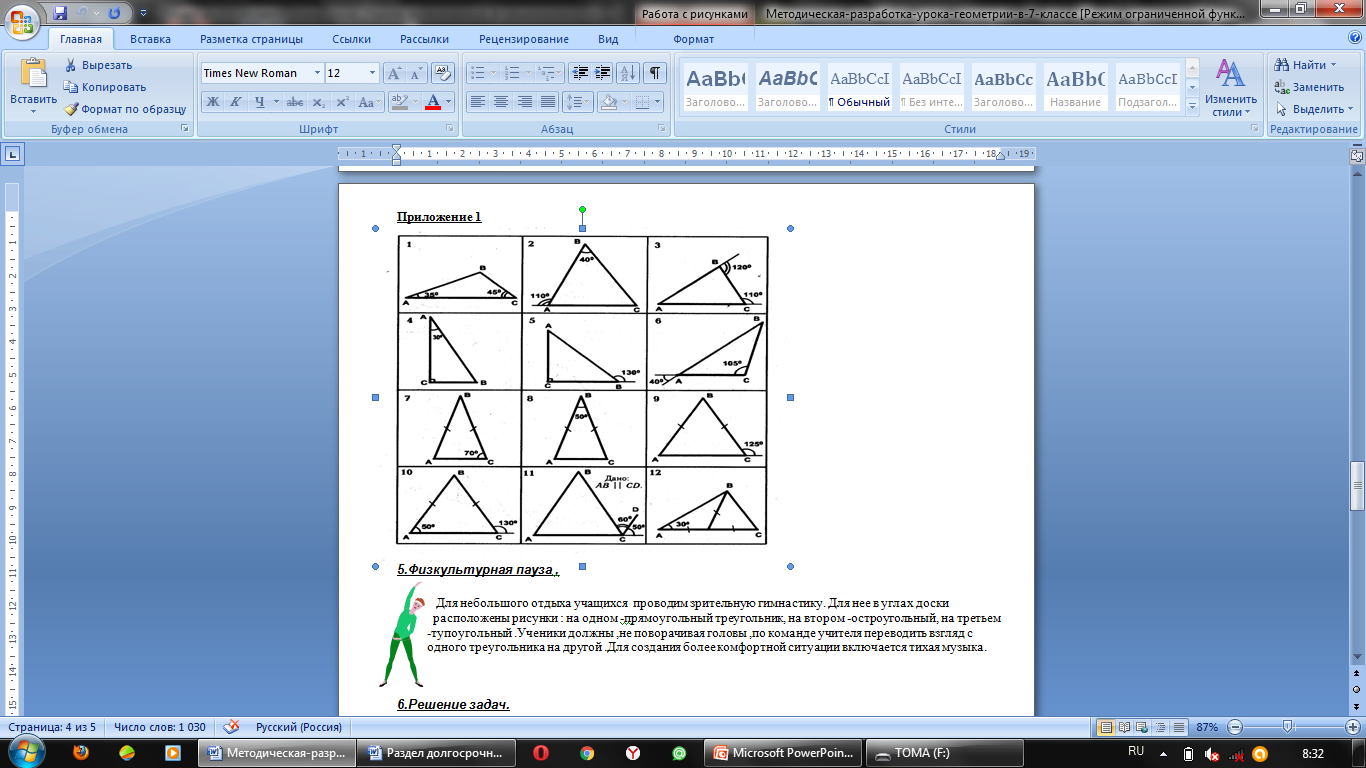
1. Графический диктант

У каждого ученика листочек для диктанта. Работа выполняется на два варианта. На вопросы учителя ученики должны отвечать либо «да», либо «нет». При ответе «да» ученик ставит значок Λ, а при ответе «нет» ставит значок _.

Цель: обучение учащихся умению применять теорию в видоизмененной ситуации, умению анализировать, сравнивать. Учащиеся учатся самооценке.

Задание. (В скобках записаны вопросы для второго варианта):

1. Сумма углов треугольника равна 90⁰ (180⁰)?

2. На рисунке 2 угол в 40⁰ (в 110⁰) является внешним углом треугольника?

3. Внешний угол треугольника равен сумме углов треугольника не смежных с ним (разности между развернутым углом и смежным с ним углом треугольника)?

4. На рисунке 1 тупоугольный треугольник (на рисунке 9 остроугольный треугольник)?

5. Прямоугольный ли это треугольник на рисунке 3 (на рисунке 1)?

6. Напротив прямого угла в треугольнике лежит гипотенуза (катет)?

7. Катетом прямоугольного треугольника является любая сторона треугольника (сторона, прилежащая к прямому углу)?

8. В треугольнике может быть только один прямой угол (только один тупой угол)?

Все рисунки для диктанта отпечатаны на отдельных листах (смотри приложение 1)

После выполнения диктанта учитель показывает какой рисунок должен получится у каждого варианта.

1вариант

2вариант

Дескрипторы:

- применяют теорему о сумме углов треугольника

- применяет определение внешнего угла треугольника.

- применяют определение развернутого и смежного углов

- применяет на практике теорему о внешнем угле треугольника.

- применяет определения остроугольного, прямоугольного и тупоугольного треугольников

- применяет теорему о сумме углов треугольника

- определяет стороны прямоугольного треугольника

- читает чертеж;

ФО: Каждый проверяет свою работу и ставит себе баллы. За каждый правильный дискриптор – 1 балл.

Дифференциация по результатам

Физкультминутка.

Для небольшого отдыха учащихся проводим зрительную гимнастику. Для неё в углах доски расположены рисунки: на одном – прямоугольный треугольник, на втором – остроугольный, на третьем – тупоугольный. Ученики должны не поворачивая головы, по команде учителя переводить взгляд с одного треугольника на другой. Для создания более комфортной ситуации включается тихая музыка.

1. Решение задач

Класс работает по группам, решая задачи, условия которых записаны и задачи на готовых чертежах. Наиболее «сильные» учащиеся работают по решению задач повышенной сложности.

Цель: формирование умения решать задачи, применяя для этого теоретический материал в нестандартной ситуации, развитие умственной математической речи учащихся.

Все. Определите вид треугольника, в котором:

- один из его углов больше суммы двух других углов

- один из его углов равен сумме двух других углов

- сумма двух любых углов больше 90⁰

- каждый из его углов меньше суммы двух других

- сумма любых двух углов меньше 120⁰.

Большинство. Найди неизвестные углы треугольника АВС (задачи № 5,6,7,8,12).

Некоторые. 1. Найти сумму внешних углов треугольника взятых по одному при каждой вершине.

1. Найти углы треугольника АВС, если ˂А: ˂В:˂С= 2:3:4. Найдите внешний угол при вершине А.

Дескриптор:

- применяют теорему о сумме углов треугольника;

- вычисляют числовые значения углов треугольника

- применяют следствия из данной теоремы

- составляют уравнение для нахождения неизвестного угла

- решают уравнение

- находят неизвестные углы

Ф.О.: взаимооценивание в форме «2 звезды 1 пожелание»

Дифференциация по уровню сложности

- поддержка слабо мотивированных учащихся со стороны учителя;

1. Самостоятельная работа

Цель: проверка умения учащимися решать задачи на применение теоремы о сумме углов треугольника и теоремы о внешнем угле треугольника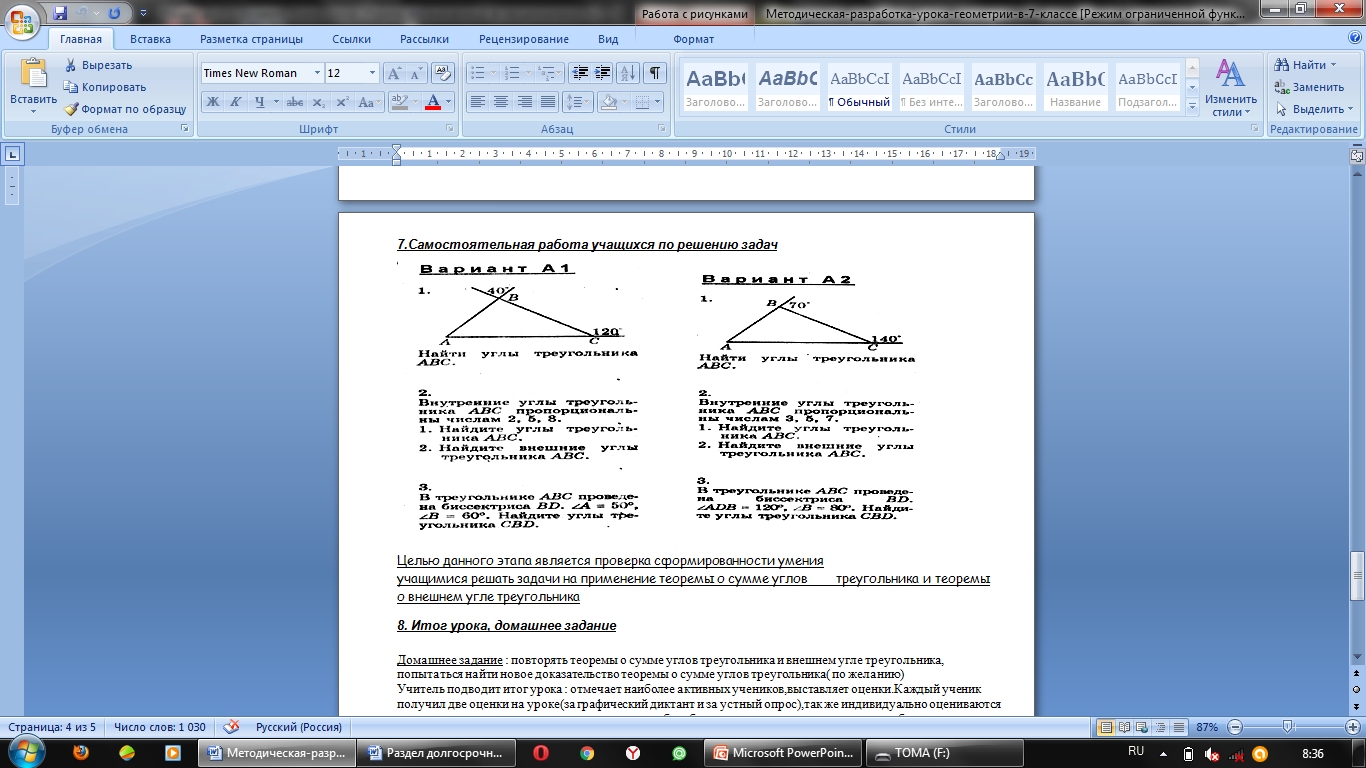

Дескрипторы:

Знание и понимание

- находят вертикальный (смежный) угол,

- находят неизвестные углы

• выполняют построение чертежа;

• используют свойство равнобедренного треугольника;

• находят градусную меру угла В

• используют теорему о сумме внутренних углов треугольника;

Применение

• пишут условие задачи и выполняют рисунок

- составляют уравнение для нахождения неизвестного угла

- решают уравнение

• находят неизвестные углы,

Анализ

• применяют определение биссектрисы угла;

• используют теорему о сумме внутренних углов треугольника;

• решают задачу.

Ф.О.: Самооценивание по дескрипторам.

Дифференциация по сложности заданий

Презентация

Слайд №1-2

Листы А-3, маркеры.

Интерактивная доска

Презентация

Слайд № 3

Карты опроса

Слайд 4 (Приложение 1)

Слайд № 5

Слайд 4 (Приложение 1)

Слайд № 6

Конец урока

2 минут

1. Подведение итогов.

«Угадай вопрос». Учащиеся по ответу, должны восстановить вопросы.

На какой вопрос можно ответить словами:

Треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник, угол треугольника.

Ф.О.: Самооценивание.

1. Рефлексия

Учащимся предлагается в устной форме ответить на вопросы, которые помогут учителю понять, насколько хорошо учащиеся усвоили изученный материал, над чем предстоит поработать на последующих уроках.

1) Что вам понравилось при изучении данной темы?

2) Что вы запомнили очень хорошо?

3) Что вызывало у вас сложность при изучении данной темы?

7. Домашнее задание.

Повторить пройденный материал.

Творческая работа. Виртуальная экскурсия « Треугольники в окружающем нас мире»

Презентация

Слайд № 7

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Поддержка в виде наводящих вопросов для слабых учащихся, и соответственно отсутствие подсказок для сильных учащихся.

Словесное поощрение, комментарии учителя, самооценивание по дескрипторам, лист самооценивани

Использование Activeboard согласно санитарным нормам, раздаточный материал

Рефлексия по уроку

Были ли цели урока/цели обучения реалистичными?

Все ли учащиеся достигли ЦО?

Если нет, то почему?

Правильно ли проведена дифференциация на уроке?

Выдержаны ли были временные этапы урока?

Какие отступления были от плана урока и почему?

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?

1:

2:

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?

1:

2:

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?

Ф.И. учащегося

Домашнее задание (max 5)

Повторение теории (max 3)

Графический диктант (max 8)

Решение задач (max 3)

Самостоятельная работа (max 3)

Итог