Презентация и разработка урока геометрии "Сумма углов треугольника". 7 класс (системно-деятельностный подход)

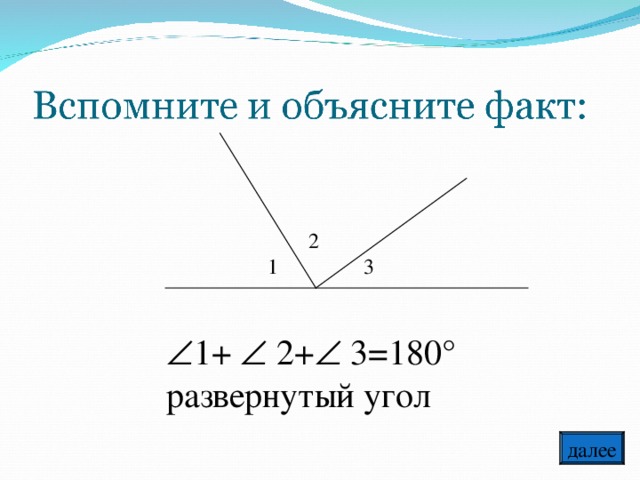
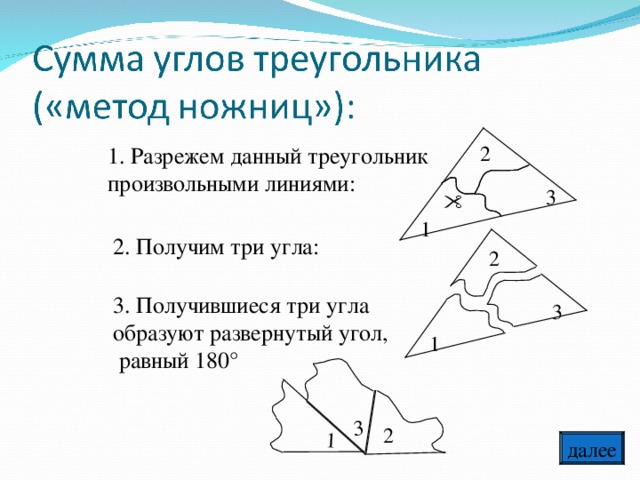
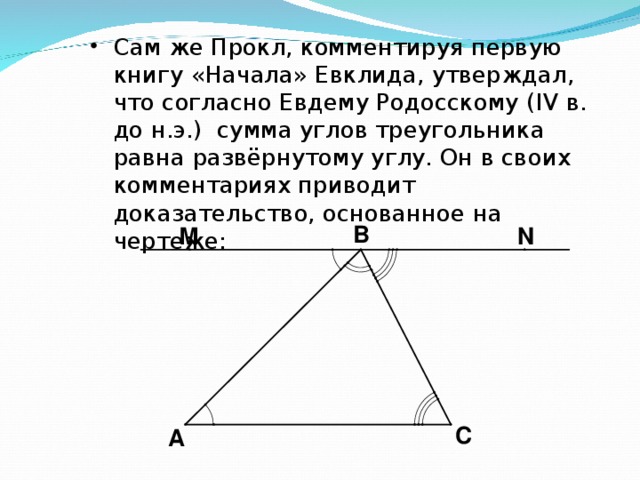
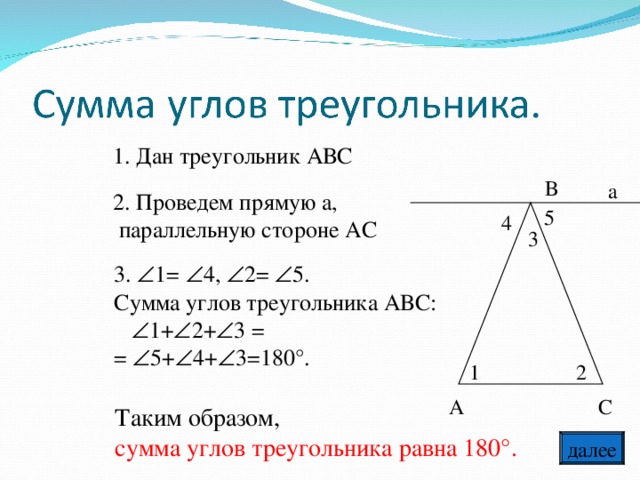
Урок по теме: «Сумма углов треугольника», 7-й класс.

Цель: развивать исследовательские навыки учащихся, навык аргументированных рассуждений, навык доказательства теорем. Практическим путем выяснить чему равна сумма углов треугольника, познакомиться с формулировкой теоремы о сумме углов треугольника, доказать теорему, научиться применять изученную теорему при решении задач;

развитие математической речи учащихся, развитие творческой активности, математических представлений;

Задачи:

- образовательные (формирование познавательных УУД):

• практическим путём выяснить, чему равна сумма углов треугольника;

• познакомиться с формулировкой теоремы о сумме углов треугольника, доказать её;

• научиться применять изученную теорему при решении задач;

• ввести понятие остроугольного, тупоугольного и прямоугольного треугольников.

- воспитательные (формирование коммуникативных и личностных УУД):

• воспитание у учащихся аккуратности, внимательности, положительного отношения к математике;

• воспитание самостоятельности и умения работать в соответствии с намеченным планом

• формировать коммуникативную компетенцию учащихся;

- развивающие (формирование регулятивных УУД)

• научить учащихся самостоятельно выдвигать гипотезу.

• совершенствование умений осознанно проводить такие приемы мышления как сравнение, обобщение и систематизация;

• умение обрабатывать информацию;

• контроль и оценка процесса и результатов деятельности;

• выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия.

Тип урока Урок первичного предъявления новых знаний.

Формы работы учащихся: Фронтальная, парная, индивидуальная

Организация деятельности учащихся на уроке:

-самостоятельно выходят на проблему и решают её;

-самостоятельно определяют тему, цели урока;

_выводят формулировку теоремы и пытаются доказать ее;

-работают с технологической картой при выполнении заданий;

-отвечают на вопросы;

-решают самостоятельно задачи;

-оценивают себя и друг друга;

-рефлектируют.

Необходимое техническое оборудование: Компьютер, проектор, раздаточный материал (технологическая карта, карточки с дополнительным заданием, карточки с домашним заданием), электронная презентация, выполненная в программе Power Point

Ход урока.

I. Организационный момент. (слайд 1)

Учитель. Здравствуйте, ребята. Кто ничего не замечает,

Тот ничего не изучает;

Кто ничего не изучает,

Тот вечно хнычет и скучает.

Сегодня вас ждет много нового и интересного. А для начала повторим уже известный вам материал.

II. Повторение

- какая фигура называется треугольником;

- какие виды треугольников вы знаете?

- назовите свойства равнобедренного треугольника, равностороннего треугольника;

- какие прямые называются параллельными, перечислите свойства параллельных прямых.

(слайды3-5)

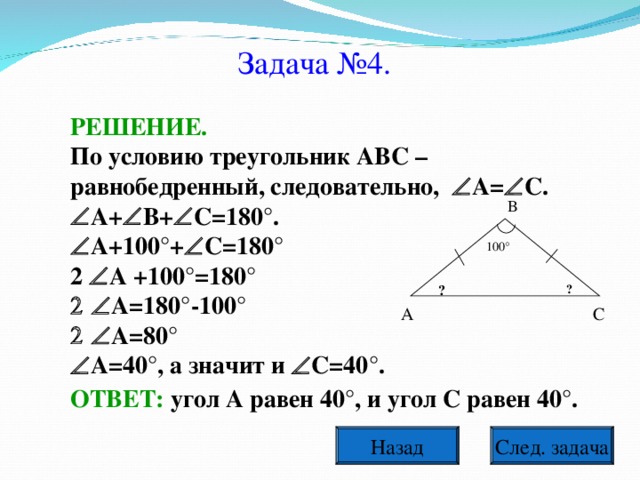
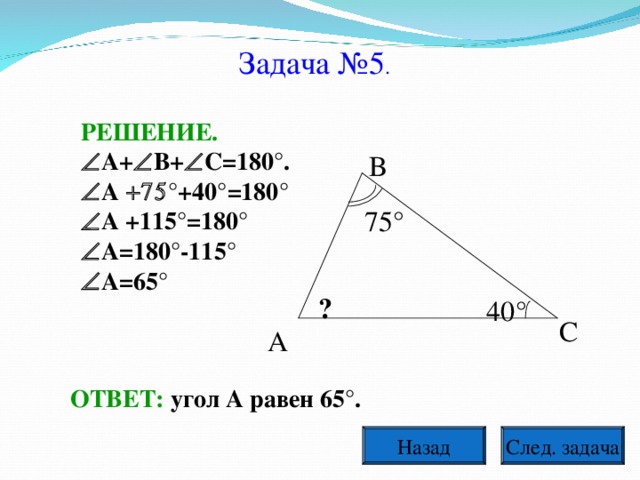
Для разминки решим следующую задачу:

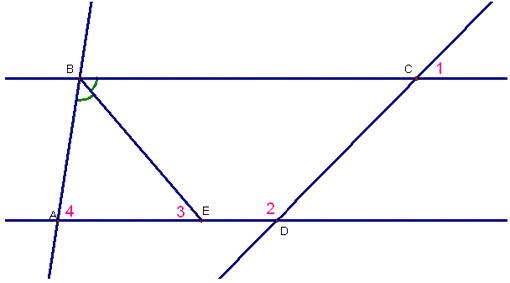
1) На рисунке 1=51⁰, 2=129⁰, 3=52⁰, ВЕ - биссектриса треугольника АВС. Найдите угол 4.

Рисунок 1

2)

Д В Е На рисунке ДЕ║АС. Найдите сумму углов

треугольника АВС.

А С

-Случайно ли сумма углов треугольника АВС оказалась равной 180˚ или этим свойством обладает любой треугольник? ( У каждого треугольника сумма углов равна 180˚).

Это утверждение носит название теоремы о сумме углов треугольника. Итак, тема нашего урока «Сумма углов треугольника». Откройте тетради и запишите её.

III. Исследовательская работа. (слайд 6,7)

Каждой группе было предложено выполнить практическое задание:

измерить с помощью транспортира углы своих треугольников. Рядом с чертежом записать результаты измерений. Найдите сумму углов каждого треугольника.

Давайте сравним полученные результаты. Какие мысли у вас возникают?

- нет огромной разницы между полученными данными;

- все треугольники были разными, а результаты почти одинаковые;

- можно предположить, что сумма углов треугольника равна 180˚;

- неужели у всех треугольников сумма углов является одной и той же величиной?

Итак, мы выдвинули гипотезу, что сумма углов треугольника равна 180˚. Но это только наше предположение. Если сумеем это утверждение доказать с помощью математических рассуждений, то это будет математический факт. Историческая справка (слайд 10-11)

-Случайно ли сумма углов треугольника АВС оказалась равной 180˚ или этим свойством обладает любой треугольник? ( У каждого треугольника сумма углов равна 180˚).

Это утверждение носит название теоремы о сумме углов треугольника. Итак, как вы думаете, какова тема нашего урока («Сумма углов треугольника»), какая цель нашего урока?

Откройте тетради и запишите тему урока.

IV. Изучение нового материала.

Итак, мы выяснили практическим путём, что сумма углов треугольника равна 180˚. Сумма углов треугольника была практическим путём установлена, вероятно, ещё в Древнем Египте. Прокол утверждал, что доказательство этого факта было известно ещё в V в. до н.э..

Возвращаемся к нашей гипотезе. Попытаемся доказать, что сумма углов треугольника равна 180˚.

- С чего мы начинаем доказательство теоремы? ( Записываем, что дано и чертим чертёж)

- Что нам дано? ( Произвольный треугольник)

-Что надо док-ть? (сумма углов =180⁰)

Учитель чертит на доске произвольный треугольник.

В

Обозначим его АВС.

Для удобства обозначим углы треугольника 1,2 и 3.

А С

Достаточно ли нам данного чертежа, чтобы доказать теорему?

Что вы можете предложить?

Достаточно ли введённых обозначений?

( Нет, недостаточно. Нужно выполнить дополнительное построение. Провести прямую а, параллельную прямой АС через точку В. Надо ещё обозначить углы 4 и 5).

Проводится доказательство теоремы.

Учитель: обсудите в парах 1) Может ли треугольник иметь:

- два прямых угла;

- два тупых угла;

- один прямой и один тупой угол ? Обоснуй ответ. Сделай вывод, запишите его в тетрадь.

2) Ребята, как вы думаете, для чего нужна эта теорема?

V. Решение задач по готовым чертежам: (слайды 16-22)

VI. Тест с последующей проверкой.

1. Могут ли в треугольнике быть 2 тупых угла?

а) да б) нет в) не знаю

1. Могут ли в треугольнике быть один угол прямой, а два другие острые?

а) да б) нет в) не знаю

1. Могут ли в треугольнике быть один угол острый, а два другие прямые?

а) да б) нет в) не знаю

4. Определите вид треугольника, если

,

а) равнобедренный, б) прямоугольный, в) не знаю

5. В EO=OF,

Найти : а)79⁰, б)69⁰, в) 59⁰ .

Ответы: 1б, 2а, 3б, 4б, 5б

VII. Подведение итогов.

Учитель. Итак, ребята, мы заканчиваем наш урок. Вы сегодня хорошо потрудились. Сами открыли чему равна сумма углов треугольника, вместе доказали теорему, решали задачи. Так чему же равна сумма углов любого треугольника? Давайте вернемся к вашим оценочным картам и подведем результаты.

VIII. Домашнее задание.

П.30-31, вопросы 1,3-5, с.84,уровень А – РТ №116-118, уровень В - №223(а, б), 225.

Кто ничего не замечает,

Тот ничего не изучает;

Кто ничего не изучает,

Тот вечно хнычет и скучает.

 1=  2

 3=  4

2

3

1

4

далее

2

1

3

 1+  2+  3=180°

развернутый угол

далее

если a||b,

то  1=  2

и  1=  3

b

3

2

1

a

Исследовательская работа

ОПЫТНЫМ ПУТЕМ ОПРЕДЕЛИТЕ, ЧЕМУ РАВНА СУММА УГЛОВ ТРЕУГОЛЬНИКОВ

• Возьмите треугольники, которые лежат у вас на столе
• Обозначьте углы этих треугольников
• Измерьте их с помощью транспортира.
• Найдите сумму этих углов
• Сделайте вывод.

2

3

1

2

1. Разрежем данный треугольник

произвольными линиями:

3



1

2. Получим три угла:

2

3. Получившиеся три угла

образуют развернутый угол,

равный 180°

3

1

далее

Случайно ли получился такой результат?

или этим свойством обладает любой треугольник?

• Свойство суммы углов треугольника было установлено эмпирически, то есть опытным путем, еще в Древнем Египте. Однако дошедшие до нас сведения об его доказательствах относятся к более позднему времени.

• Древнегреческий ученый Прокл (410 – 485 г.г. н.э.) утверждает, что согласно Евдему Родосскому, это доказательство было открыто еще пифагорейцами в 5 веке до нашей эры.

29.10.16

6

• Сам же Прокл, комментируя первую книгу «Начала» Евклида, утверждал, что согласно Евдему Родосскому ( IV в. до н.э.) сумма углов треугольника равна развёрнутому углу. Он в своих комментариях приводит доказательство, основанное на чертеже:

1. Дан треугольник АВС

В

а

2. Проведем прямую а,

параллельную стороне АС

5

4

3

3.  1=  4,  2=  5.

Сумма углов треугольника АВС:

 1+  2+  3 =

=  5+  4+  3=180°.

2

1

С

А

Таким образом,

сумма углов треугольника равна 180°.

далее

Может ли треугольник иметь:

• два прямых угла;
• два тупых угла;
• один прямой и один тупой угол ?

Обоснуй ответ .

Сделай вывод .

далее

Вывод:

В любом треугольнике либо

все три угла острые;

либо два угла острые,

а третий – тупой или прямой.

Найти углы треугольника:

?

?

?

Решение

Существует ли треугольник ABC,

у которого

 A = 40°,  B = 60°,  C = 70°?

Решение

Найти угол треугольника:

В

?

70°

А

С

Решение

Найти углы треугольника:

В

100°

?

?

С

А

Решение

Задача №5.

Найти угол треугольника:

В

75°

?

40°

С

А

Решение

Задача №6.

Найти угол треугольника:

В

?

38°

А

С

Решение

Задача №7.

Найти углы треугольника:

В

?

?

А

С

Решение

Задача №1.

РЕШЕНИЕ.

У треугольника все стороны равны, а против равных сторон лежат равные углы, значит искомый угол равен 180°:3, т.е. равен 60°.

ОТВЕТ: углы треугольника равны 60°.

След. задача

Назад

Задача №2.

РЕШЕНИЕ.

 A+  B+  C = 40°+ 60°+ 70°=170°.

Но сумма углов треугольника равна 180°, следовательно треугольника с данными углами не существует.

ОТВЕТ: не существует

След. задача

Назад

Задача №3.

РЕШЕНИЕ.

Треугольник АВС равнобедренный, т.к. АВ=ВС, значит  С=  А = 70°.

А+  В+  С=180°.

70°+  В+70°=180°

140°+  В=180°

 В=180°-140°

 В=40°

В

?

70°

А

С

ОТВЕТ: угол В равен 40°.

След. задача

Назад

Задача №4.

РЕШЕНИЕ.

По условию треугольник АВС – равнобедренный, следовательно,  А=  С.

 А+  В+  С=180°.

 А+100°+  С=180°

2  А +100°=180°

 А=180°-100°

 А=80°

 А=40°, а значит и  С=40°.

В

100°

?

?

А

С

ОТВЕТ: угол А равен 40°, и угол С равен 40°.

След. задача

Назад

Задача №5 .

РЕШЕНИЕ.

 А+  В+  С=180°.

 А  °+40°=180°

 А +115°=180°

 А=180°-115°

 А=65°

В

75°

?

40°

С

А

ОТВЕТ: угол А равен 65°.

След. задача

Назад

Задача №6.

РЕШЕНИЕ.

В треугольнике АВС,  А=90°.

 А+  В+  С=180°.

 °  В+38°=180°

 В  +128°=180°

 В=180°-128°

 В=52°

В

?

38°

А

С

ОТВЕТ: угол В равен 52°.

След. задача

Назад

Задача №7.

РЕШЕНИЕ.

В треугольнике против равных сторон лежат равные углы, значит  В=  С, а  А=90°.

 А+  В+  С=180°.

 °+  В+  С=180°

90°+2  В=180°

 В=180°-90°

 В=90°

 В=45°, а значит и  С=45°.

В

?

?

А

С

ОТВЕТ: угол В равен 45°, и угол С равен 45°.

След. задача

Назад

Участвовал в открытии нового

Справился с затруднением

Выполнял правила работы в паре, группе .

Все получилось !

Надо тренироваться