| Этапы урока | Цель этапа | Деятельность учителя | Деятельность учащихся | УУД |
| Организационный момент | Создание условий у учащихся внутренней потребности включения в учебную деятельность | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
– Чему мы научились на прошлых уроках?
– Как вы думаете, какие действия с дробями мы еще не освоили? – Верно, сегодня на уроке мы продолжим учиться работать с дробями. | Включаются в деловой ритм урока.
– Складывать и вычитать дроби и смешанные числа.
– Умножение и деление дробей. | Личностные: Регулятивные: Коммуникативные:
|
| Актуализация знаний
| Актуализация учебного содержания, необходимого и достаточного для восприятия нового материала: сокращение дробей, сложение и вычитание дробей с одинаковыми знаменателями, периметр и площадь прямоугольника; | 1. Назовите все числа, взаимно простые с числом 12 и меньшие его. – Всегда ли взаимно простые числа сами являются простыми? Приведите примеры. – Как связаны между собой понятия взаимно простых чисел и сокращение дробей? – Сократите дроби: 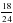 ; ;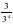 ; ; 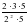 ; ;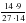 . . 2. – Найдите t, если: 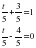 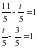
– Найдите и зачеркните полученные результаты в таблице: | 30 | 11 | 3 | 26 | 17 | 21 | | 2 | 15 | 23 | 14 | 8 | 20 | | 5 | 16 | 1 | 18 | 12 | 9 | | 4 | 10 | 24 | 27 | 6 | 29 | | 22 | 13 | 28 | 7 | 19 | 25 |
– Последовательно соедините точки отрезками и достройте полученную ломаную линию до четырехугольника. – Чем интересен этот четырехугольник? – Назовите свойства прямоугольника, которые вы знаете. – Как найти его периметр, площадь? Запишите соответствующие формулы. 3. Индивидуальное задание
| – 5; 7; 11.
– Нет.
Учащиеся приводят примеры - Если в числителе и знаменателе взаимно простые числа, то дробь несократима
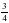 ; ; 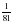 ; ; 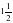 ; ; 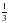
– 2; 4; 6; 8
| 30 | 11 | 3 | 26 | 17 | 21 | |  2 2
| 15 | 23 | 14 | 8 | 20 | | 5 | 16 | 1 | 18 | 12 | 9 | | 4 | 10 | 24 | 27 | 6 | 29 | | 22 | 13 | 28 | 7 | 19 | 25 |
– Это прямоугольник.
– Противоположные стороны равны, углы прямые
P = (a + b) 2; S = ab.
| Познавательные: Коммуникативные:
|
| Постановка учебной проблемы | Формирование познавательных мотивов учебной деятельности: стремление открыть знания, приобрести умения. | Задача. Ширина прямоугольника равна 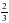 дм, а его длина – 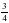 дм. Вычислите периметр и площадь этого прямоугольника. дм. Вычислите периметр и площадь этого прямоугольника. | Самостоятельное выполнение. | Регулятивные УУД: Уметь принимать решение в проблемной ситуации. Познавательные УУД Уметь преобразовывать информацию из одной формы в другую.
|
| Выявление причины затруднения и постановка цели деятельности | организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности: формулу нахождения площади знаем, а правила умножения дробей не знаем. | Проверка решений
– Чему равна площадь этого прямоугольника?
– Какое задание вы должны были выполнить? – Почему вы не смогли выполнить это задание? В чём затруднение?
– Какую цель мы поставим перед собой? – Для чего нам нужен алгоритм?
– Как бы вы назвали тему урока? – Молодцы! Вы точно определили тему и цель нашего урока, запишите тему в тетрадь. | – Периметр прямоугольника равен дм. Учащиеся дают разные ответы
– Найти площадь прямоугольника
– Для того, чтобы найти площадь надо длину умножить на ширину, т.е. перемножить дроби 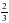 и и 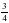 , а мы еще не умеем умножать дроби. , а мы еще не умеем умножать дроби. – Вывести алгоритм умножения дробей. – Чтобы научиться умножать дроби
– Умножение дробей
| Регулятивные: формирование умения отличать новое знание от уже известного формирование умения высказывать своё предположение на основе имеющихся знаний формирование умения оценивать учебные действия в соответствии с поставленной задачей Коммуникативные: Личностные: |
| Построение проекта выхода из затруднения | организация коммуникативного взаимодействия для построения нового способа действия, устраняющего причину выявленного затруднения | – У кого есть идеи? (Если гипотез не последует, то предложить учащимся выполнить следующую работу). – Для того, что бы достичь намеченной цели, выполним практическую работу. – Рассмотрим квадрат со стороной 1 дм. Разделим его ширину на три равные части, а длину – на четыре. На сколько частей разбит квадрат? У каждого на столе рисунок: |
|
|
|
| 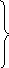
| |
|
|
|
| 1 дм | |
|
|
|
|
|
– Что вы можете сказать о закрашенном прямоугольнике? – Как вы можете выполнить данное задание?
– Чему равна площадь большого квадрата?
– Чему равна площадь маленького квадрата?
– Чему равна площадь закрашенной фигуры и почему?
– Запишите выражение для нахождения площади данного прямоугольника. – Какой вывод можно сделать? – Посмотрите на равенство. Как оно могло получиться?
– Запишем на математическом языке, то, что вы сейчас проговорили – Сделайте вывод. Что является произведением дробей?
– Запишите правило в общем виде.
– Какими, должны быть числа a,b,c,d? – Молодцы! Давайте прочитаем правило умножения дробей в учебнике, стр. 57. – Что можно сделать с получившейся дробью? – А можно было произвести сокращение до получения результата? – Сформулируйте алгоритм умножения дробей
– Очень хорошо! |
– На 12 равных частей
– Это прямоугольник, площадь, которого нам надо найти.
– Определить, какую часть этот прямоугольник составляет от площади квадрата.
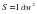
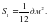
– Площадь закрашенной фигуры 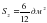 , так как она состоит из 12 маленьких квадратов, площадь каждого квадрата , так как она состоит из 12 маленьких квадратов, площадь каждого квадрата 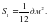
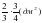 . .
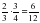 . .
– Числитель 6 – это произведение числителя 2 и числителя 3, а знаменатель 12 – это произведение знаменателя 3 и знаменателя 4. 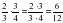 . .
– Произведением двух дробей является дробь, числитель, которой равен произведению числителей, а знаменатель – произведению знаменателей. 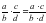
– Натуральными
Учащиеся читают правило в учебнике
– Её можно сократить
- Да можно сократить дробь 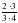 = = 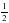
Произведение дробей записать в виде дроби, в числители, которой записано произведение числителей, в знаменателе произведение знаменателей. Если возможно сократить, получившуюся дробь. Найти произведение чисел, стоящих в числителе и чисел, стоящих в знаменателе. Если получилась неправильная дробь, выделить целую часть. | Познавательные: формирование умения извлекать информацию из иллюстраций формирование умения на основе анализа объектов делать выводы формирование умения вести поиск и выделять необходимую информацию способность структурировать найденную информацию в нужной форме Регулятивные: Коммуникативные: Личностные: |
| Первичное закрепление во внешней речи | Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: умножение дробей. | – Посмотрим на практике, как мы разобрались в новой теме. Выполните № 289 (а, б) (Решение выполнять на доске с проговариванием алгоритма)
№ 289 (в, г) – в парах, проверка по образцу (образец заранее заготовлен на закрытой части доски) в) 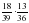 = =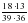 = =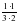 = =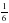 г) 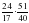 = =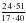 = =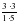 = =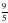 =1 =1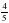 | а) 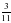 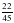 = = 1) произведение дробей записать в виде дроби, в числителе которой записано произведение числителей, а в знаменателе произведение знаменателей: 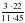 = = 2) сократим дробь: 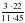 = = 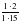 3) Найдём произведение в числителе и знаменателе: 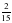 б) 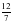 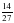 = = 1) произведение дробей записать в виде дроби, в числители которой записано произведение числителей, а в знаменателе произведение знаменателей: 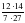 = = 2) сократим дробь: 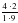 = = 3) Найдём произведение в числителе и знаменателе: 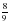 Учащиеся выполняют задание в тетрадях. Проверка
| Познавательные: Регулятивные: Коммуникативные: формирование умения сотрудничать с другими людьми в поиске необходимой информации формирование умения постановки вопросов, разрешение конфликтов формирование умения управлять поведением партнёра точностью выражать свои мысли Личностные: |
| Самостоятельная работа с самопроверкой по эталону | Установление правильности и осознанности изучения темы. Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу. | – Теперь выполните задание самостоятельно: № 289 (д, е) - Чем отличается это задание от предыдущего? - Как Вы думаете, распространяется ли правило умножения дробей на произведение состоящее более чем из двух множителей?
- Выполняем задание. Работа проверяется по эталону. Если задание выполнено правильно, то учащиеся ставят знак «+», если допущена ошибка, то знак «?». После проверки учитель выясняет причину допущенных ошибок, и ребята исправляют ошибки. д)  ; ; е) 
|
– Произведение трех дробей
– Думаем, что распространяется.
| Регулятивные:
|
| Включение в систему знаний и повторение | тренировка навыков использования нового содержания совместно с ранее изученным | № 291 по одному ученику у доски.
| 1)  ; ; 2)  – длина – длина  (см2) – площадь прямоугольника. (см2) – площадь прямоугольника. 3)  4)  – высота – высота  (дм3) (дм3)
| Регулятивные: Личностные УУД |
| Рефлексия | Оценка собственной деятельности на уроке. Фиксация неразрешённых затруднений как направления будущей учебной деятельности | – Что нового вы узнали на уроке? – Какой метод вы использовали для «открытия» правила умножения дробей? – Что у вас сегодня получалось? – Как бы вы оценили свою работу? Карточки на столах у детей.
| – Как умножают дроби.
В карточке оценивают свою деятельность | Познавательные: Регулятивные: Личностные: формирование умения высказывать соё отношение к уроку, выражать свои эмоции формирование мотивации к обучению и целенапраленной познавательной деятельности |
| Домашнее задание | Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания. | п. 3.2.3 стр. 57, № 340, 349, 356
| Записывают домашнее задание в дневник. |
|
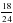 ;
;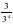 ;
; 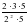 ;
;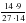 .
.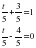
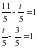
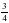 ;
; 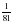 ;
; 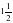 ;
; 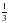
 2
2

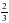
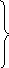
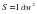
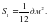
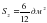 , так как она состоит из 12 маленьких квадратов, площадь каждого квадрата
, так как она состоит из 12 маленьких квадратов, площадь каждого квадрата 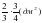 .
.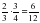 .
.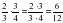 .
.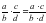
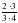 =
= 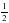
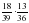 =
=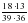 =
=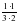 =
=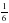
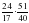 =
=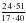 =
=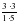 =
=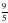 =1
=1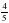
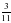
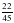 =
=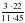 =
=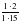
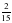
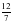
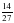 =
=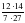 =
=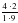 =
=