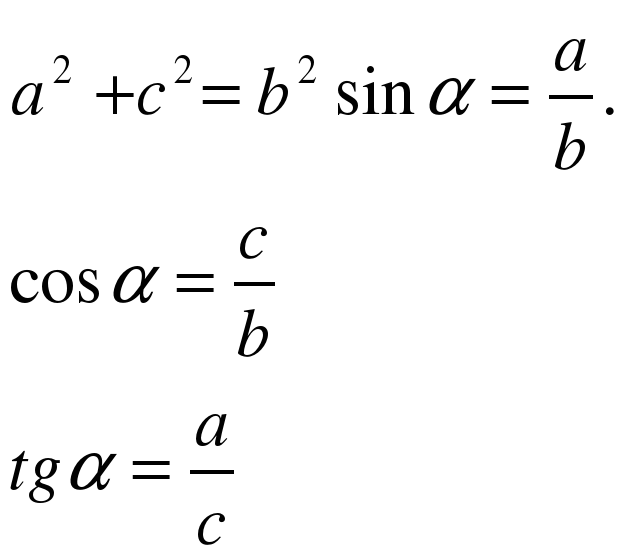Урок по теме: «Решение треугольников».
( 9 класс, УМК- А.В. Погорелов, «Геометрия 7-9.)
Данный урок построен в технологии «Критического мышления через чтение и письмо», что позволяет максимально использовать активность учащихся. Особенность урока – рефлексивная деятельность учащихся: осмысление «пробелов» знаний, поиск необходимой информации для восполнения знаний учащихся через решение заданий и новый уровень оценки собственной деятельности.
Место урока в курсе изучения геометрии по учебнику «Геометрия 7-9» автор А.В. Погорелов.В восьмом классе рассматривается тема: «Решение прямоугольных треугольников», на изучение которой отводится 16 часов.
Просмотр содержимого документа
«Пояснительная записка»
Урок по теме: «Решение треугольников».
( 9 класс, УМК- А.В. Погорелов, «Геометрия 7-9.)
Данный урок построен в технологии «Критического мышления через чтение и письмо», что позволяет максимально использовать активность учащихся. Особенность урока – рефлексивная деятельность учащихся: осмысление «пробелов» знаний, поиск необходимой информации для восполнения знаний учащихся через решение заданий и новый уровень оценки собственной деятельности.
Место урока в курсе изучения геометрии по учебнику «Геометрия 7-9» автор А.В. Погорелов.В восьмом классе рассматривается тема: «Решение прямоугольных треугольников», на изучение которой отводится 16 часов.
| 8 класс |
|
| Теорема Пифагора | 16 |
| Косинус угла | 1 |
| Теорема Пифагора | 2 |
| Египетский треугольник | 1 |
| Перпендикуляр и наклонная | 1 |
| Неравенство треугольников | 1 |
| Решение задач по теме: «Теорема Пифагора» | 1 |
| Контрольная работа № 3 по теме: «Теорема Пифагора» | 1 |
| Соотношение между сторонами и углами в прямоугольном треугольнике | 2 |
| Основные тригонометрические тождества | 2 |
| Значение синуса, косинуса и тангенса некоторых углов | 2 |
| Изменение синуса, косинуса и тангенса при возрастании угла | 1 |
В девятом классе изучается тема: «Решение треугольников», на которую отводится 10 часов. На данный урок отводится 2 часа и проходит он после изучения теоремы синусов, косинусов и соотношения между углами треугольника и противолежащими сторонами.
| 9 класс |
|
| Решение треугольников (10 часов ) | 10 |
| Теорема косинусов. | 2 |
| Теорема синусов. | 2 |
| Соотношение между углами треугольника и противолежащими сторонами. | 1 |
| Решение треугольников | 4 |
| Контрольная работа № 3 по теме «Решение треугольников». | 1 |
Технология «Развитие критического мышления через чтение и письмо»
1.Возникла в Америке в 80-е годы ХХ столетия. В России технология известна с конца 90-х годов и по-другому называется «Чтение и письмо для развития критического мышления» (Reading and Writing for Critical Thinking – ЧПКМ). В основу ее положены идеи и положения теории Ж. Пиаже об этапах умственного развития ребенка, Л.С. Выгодского, о зоне ближайшего развития и о неразрывной связи обучения и общего развития ребенка. К. Поппера и Р. Пола, об основах формирования и развития критического мышления. Э. Браун и И. Бек, о метакогнитивном учении гражданского и правового образования и др. Разработчики технологии ЧПКМ смогли «переложить» положения данных теорий на язык практики, причем довели свою работу до уровня педагогической технологии, выделив этапы, методические приемы и критерии оценки результата. Именно поэтому их разработками может пользоваться огромное количество педагогов, достигая эффективных результатов в работе.
2.Идеи технологии ЧПКМ:
Дети от природы любознательны, они хотят познавать мир, способны рассматривать серьезные вопросы и выдвигать оригинальные идеи.
Роль учителя – быть вдумчивым помощником, стимулируя учащихся к неустанному познанию и помогая им сформировать навыки продуктивного мышления.
Критическое мышление формируется, прежде всего, в дискуссии, письменных работах и активной работе с текстами. С этими формами работы учащиеся хорошо знакомы, их необходимо только несколько изменить.
Существует неразрывная связь между развитием мыслительных навыков и формированием демократического гражданского сознания.
3. Определение технологии ЧПКМ. (Дэвид Клустер – профессор, преподаватель американской литературы Хоуп-колледжа, Холланд, штат Мичиган, США, доброволец программы РКМЧП в Чешской Республике и Республике Армения.) Определение состоит из пяти пунктов.
-критическое мышление есть мышление самостоятельное. ,
-информация является отправным, а отнюдь не конечным пунктом критического мышления.
-критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить.
-критическое мышление стремится к убедительной аргументации. Центром аргументации, является утверждение. Утверждение поддерживается рядом доводов. Каждый из доводов, в свою очередь, подкрепляется доказательствами.
- критическое мышление есть мышление социальное.
Все пять пунктов этого определения критического мышления могут воплощаться в различных видах учебной деятельности, но наилучшим из них является, письменная работа – как для учителей, так и для учащихся. На письме процесс мышления становится видимым и, следовательно, доступным для учителя. Пишущий всегда активен. Он всегда мыслит самостоятельно и пользуется при этом всем имеющимся у него багажом знаний. Он выстраивает достойную аргументацию для подкрепления своего мнения.
План урока и распределение времени урока
| Содержание этапов урока | Виды и формы работы | Время в минутах. |
| 1.Организационный момент. | 1.Приветствие учащихся.
2. Настрой учащихся на рабочий режим. 3.Организация рабочего места | 2мин. |
| 2.Актуализация знаний по теме «Решение прямоугольных треугольников» Стадия вызова. | Диктант. Повторение некоторого теоретического материала по теме: «Прямоугольный треугольник». Индивидуальная работа и последующая проверка. Тест можно показать на экране интерактивной доски. (Самооценка по готовым ответам) | 5 мин. |
| 3.Обобщение и коррекция опорных знаний по теме «Решение прямоугольных треугольников» Стадия вызова. | Составление и заполнение таблиц учителем на доске и учащимися в тетрадях по теме: «Решение прямоугольных треугольников». Обсуждение в парах. Что я знаю по данной теме? | 5мин. |
| 4.Формулировка цели урока. Определение знаний, необходимых для реализации цели. | Учащиеся формулируют тему урока и цель. Работа в парах по определению знаний теоретического материала по новой теме (учащимися на листах записываются необходимые формулы, которые впоследствии учителем записываются на доске). Что я знаю по данной теме? | 5мин. |
| 5.Учащиеся разбиваются на группы по 4 человека. Каждому ученику присваивается свой номер. Ученики с одинаковыми номерами объединяются в новые группы. Каждая группа решает одну из четырех задач по теме: «Нахождение трех элементов треугольника по трем известным». Работа с текстом по группам (метод «Зигзаг»). Стадия осмысления. | Работа в группах. Решение осуществляется по составленной учителем программе-алгоритму. Каждая группа решает задачу одного вида. | 10мин. |
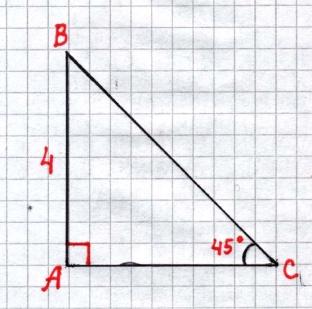
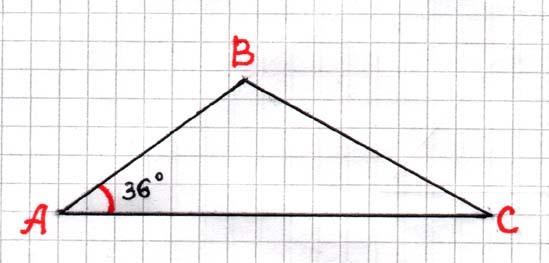
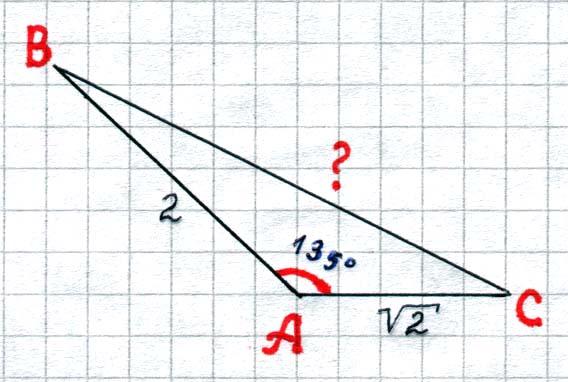
| 6.Решение задач на нахождение неизвестных элементов треугольника по трем известным. Стадия первоначального использования полученных знаний (действие по образцу) | Каждой группе предлагается на выбор треугольник. У выбранного треугольника необходимо измерить три элемента, а остальные вычислить. Работа в группах. Измерить остальные три элемента и сравнить с результатами вычислений. Оценить свою работу. | 7мин. |
| 7.Меняются группы. Каждый возвращается в свою первоначальную группу. Каждый ученик группы объясняет решение своей задачи. | Рассматривается ход решения каждой задачи. Каждому ученику выставляется группой оценка за объяснение нового материала по теме: «Решение треугольников». | 12мин. |
| 8.Все члены группы заполняют таблицы формул. | Каждой группе в начале работы выдавалась таблица, которую в конце работы учащиеся должны заполнить. Выписать все необходимые для решения формулы. Учитель выписывает таблицы на доске или показывает на экране интерактивной доски. | 4мин. |
| 9.Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач Стадия рефлексии. | Решение задач из сборника ЕГЭ (работа в тетрадях), с последующей проверкой. Выполнение тестовых заданий. (проверь себя по готовым ответам) | 10мин. |
| 10.Решение задач с практическим содержанием из учебника. | Фронтальная работа. | 10мин. |
| 11. Подведение итогов урока. синквейн | Правила составления синквейна.
| 5мин. |
| 12.Домашняя работа. | Решить задачи из таблицы по теме: «Решение треугольника». Составить Памятку по теме: «Решение треугольников». | 3мин. |
| 13.Выставление оценок. | Заполнение таблицы оценок. Результирующая оценка: среднее арифметическое . Оценку выставляет ученик. | 2мин. |
Просмотр содержимого документа
«Приложение 1. Тест.»
Просмотр содержимого документа
«Приложение 3-6»
Просмотр содержимого документа
«Приложение 7.»
Просмотр содержимого документа
«Приложение № 11. Синквейн.»
Приложение №11. Подведение итогов урока. синквейн- стихотворение по алгоритму: - развивают поэтические способности учеников.
Синквейн- самая легкая форма стихотворений по алгоритму. Дети всех возрастов с удовольствием сочиняют синквейны, но к старшим классам синквейны обретают более глубокое содержание. Перед изучением вводной темы по творчеству А Островского «Театр Островского» на стадии вызова ученица составила синквейн:
Театр.
Волнующий, загадочный.
Завораживает, будоражит, тревожит.
Театр никого не оставляет равнодушным.
Сама жизнь
Синквейн. Способность резюмировать информацию, излагать сложные идеи, чувства и представления в нескольких словах – важное умение. Оно требует вдумчивой рефлексии, основанной на богатом понятийном запасе .
Синквейн – это стихотворение, которое требует синтеза информации и материала в кратких выражениях. Слово синквейн происходит от французского, которое означает «пять». Таким образом, синквейн – это стихотворение, состоящее из пяти строк.
План написания синквейна следующий:
1.Первая строка – тема стихотворения, выраженная одним словом, обычно именем существительным;
2. Вторая строка – описание темы в двух словах, как правило, именами прилагательными;
3. Третья строка – описание действия в рамках этой темы тремя словами, обычно глаголами;
4. Четвертая строка – фраза на тему синквейна из четырех слов, выражающая отношение автора к данной теме;
5. Пятая строка – одно слово – синоним к первому, на эмоциональном или филосовско-обобщенном уровне повторяющее суть темы.
Приведем пример синквейна, который составили студенты 1 курса факультета психологии по завершению изучения темы «Множества»:
Множества
Конечные бесконечные
Не пересекаются совпадают пересекаются
Элементы множества обладают свойствами
Совокупности.
Треугольник.
Значимый, актуальный.
Измерять, вычислять, чертить.
«Любовный треугольник».
Часть любой фигуры..
Просмотр содержимого документа
«Приложение №12.»
Просмотр содержимого документа
«Приложение №13.»
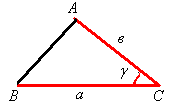
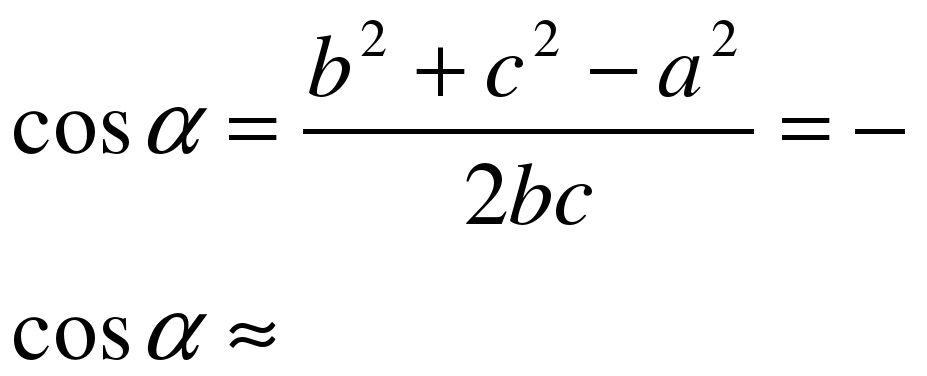
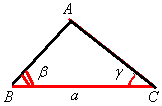
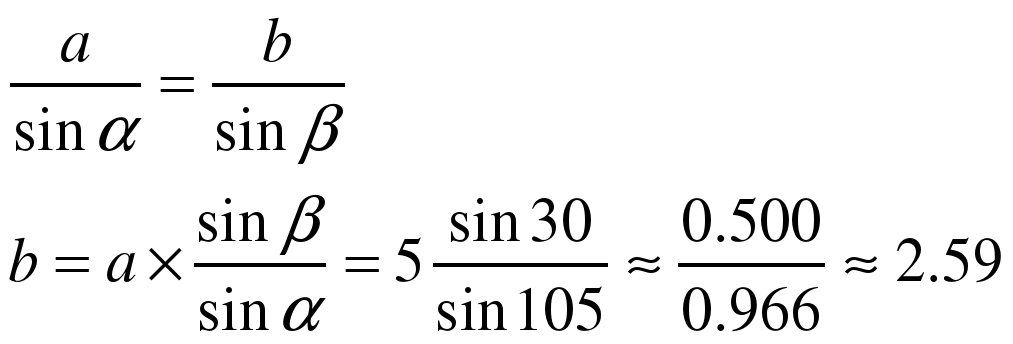
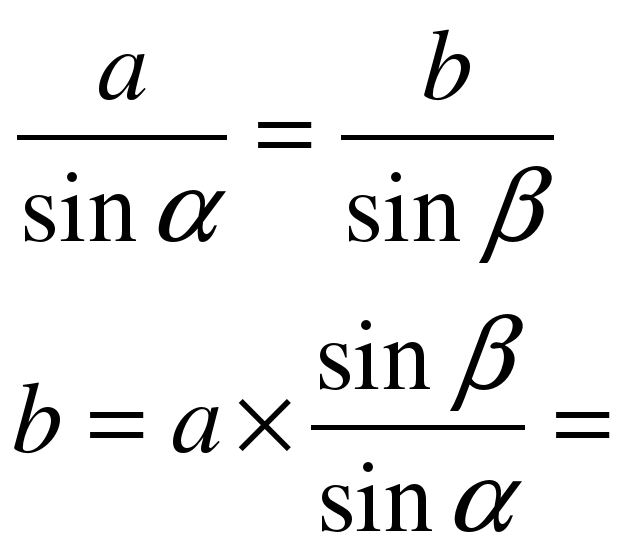
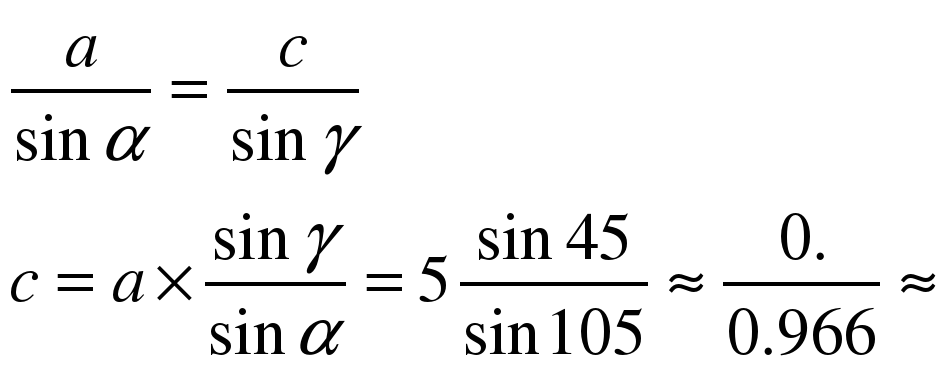
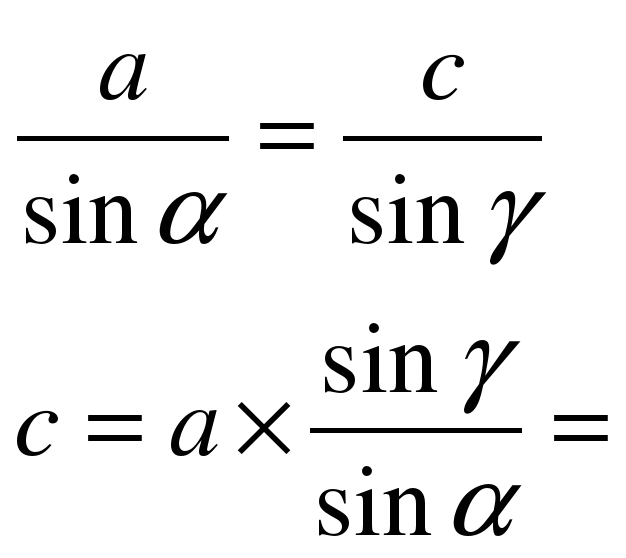
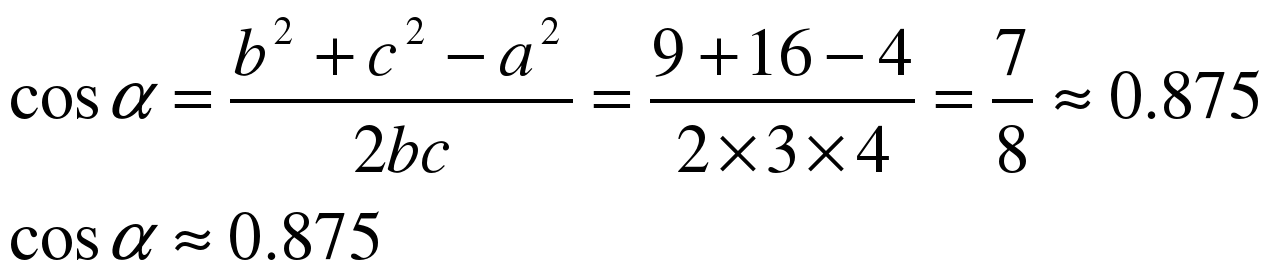
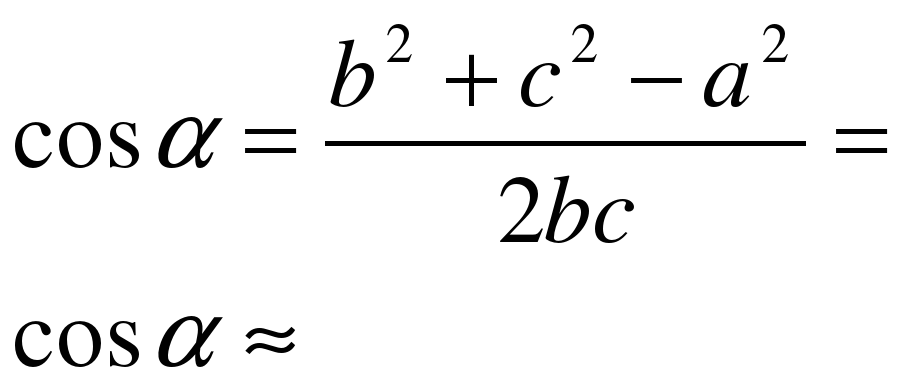

 А
А

 А
А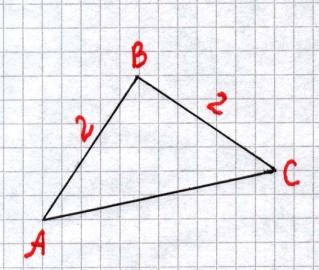

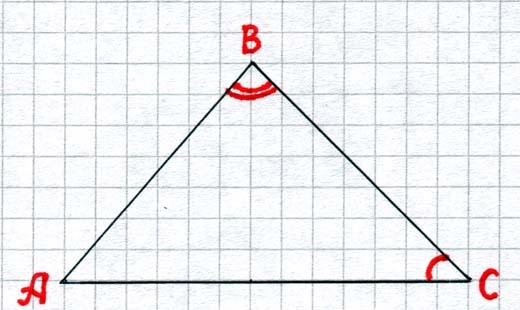
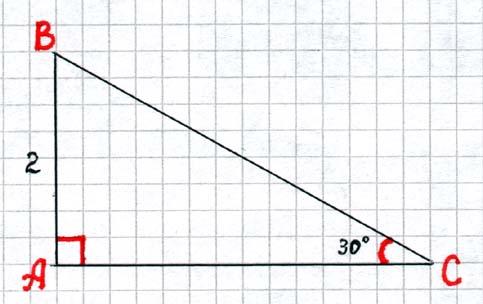
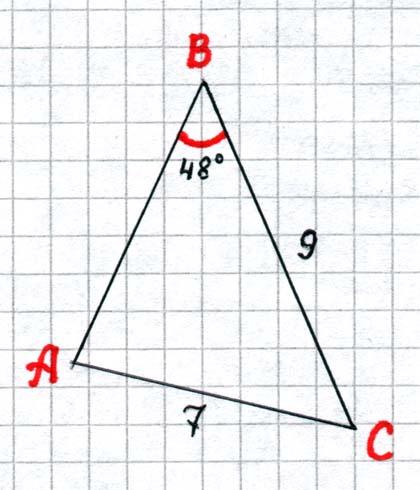

 А 1) Теорему о сумме углов в треугольнике:
А 1) Теорему о сумме углов в треугольнике:
 А
А