План-конспект урока в 9 классе с использованием ЦОР
«Площадь круга и его частей»
Выполнила: Шевцова Оксана Александровна
учитель математики и информатики
МБОУ СОШГ Лермонтовского сельского поселения
Хабаровск, 2015Тема: «Площадь круга и его частей».
Форма урока – комбинированный.
Характеристика содержания учебного материала темы:
На данном уроке учащиеся будут иметь дело со следующими понятиями:
площадь фигуры;
вписанная и описанная окружности правильного n-угольника;
площадь треугольника;
площадь правильного n-угольника;
круг;
площадь круга;
круговой сектор;
площадь кругового сектора;
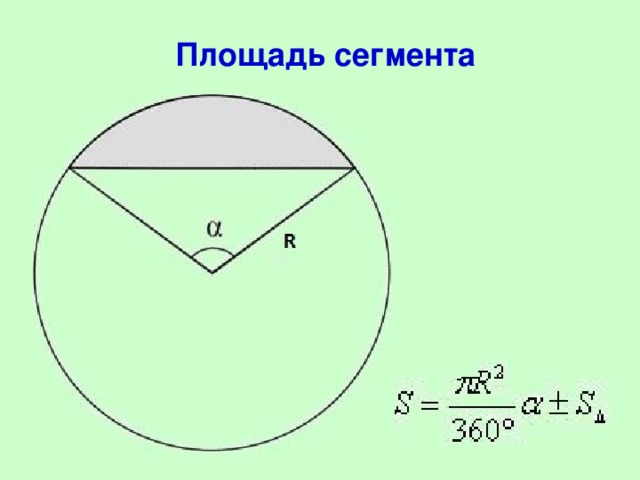
сегмент;
площадь сегмента.
Из перечисленных понятий новыми для учащихся являются: круговой сектор; площадь кругового сектора; сегмент; площадь сегмента. Остальные были на предыдущих уроках или в предыдущих классах.
На уроке вводятся два новых утверждения: площадь кругового сектора и сегмента. При введении данных утверждений необходимо вспомнить площадь круга, треугольника. Словесные формулировки данных утверждений отсутствуют, дается только их буквенная запись.
Цели:
ОЦ – обеспечить усвоение учащимися определений круга, сектора, сегмента; вспомнить определения понятий, связанных с данной темой; помочь учащимся запомнить формулы нахождения площади круга и его частей, а также понимание учащимися их вывода.
ВЦ – воспитать познавательную активность.
РЦ – развивать внимание, наглядно-образное мышление.
Учебные задачи:
получить представление о выводе формулы площади круга и площади сектора;
понять и попытаться запомнить формулы нахождения площади круга и его частей;
научиться применять эти формулы при решении простейших практических задач.
План урока:
Организационный момент – 2мин.
Актуализация – 5мин.
Мотивация и подведение учащихся к новому – 4мин.
Введение нового – 16мин.
Первичное закрепление – 15мин.
Подведение итогов – 3мин.
Ход урока.
Организационный момент.
Сегодня на уроке мы продолжим изучать различные фигуры, а именно изучим круг и его части. Запишите, пожалуйста, тему урока «Площадь круга и его частей».

Актуализация.
Давайте теперь вспомним то, что уже изучали и ответим на следующие вопросы.

| Деятельность учителя | Деятельность ученика |
| Что такое площадь фигуры? | Дети затрудняются ответить, так как материал был давно изучен. Площадь – это положительное число, означающее, сколько квадратных единиц или его частей содержится в фигуре. |
| Какую фигуру называют кругом? Начертите в тетради круг. | Многие дети справляются с ответом на этот вопрос, так как ответ основан на предыдущем. Круг – часть плоскости, ограниченная окружностью. |
| Чему равно число π? | Дети с легкостью отвечают на этот вопрос, так как это число использовалось на предыдущем занятии. π=3,14 |
| Как понимается «одно значение стремится к другому»? | Данный вопрос вызовет затруднения. Ученики с помощью учителя рассуждают на данную тему. Если при увеличении одного значения, оно становится близким ко второму, то говорят, что одно значение стремится ко второму. Приводятся примеры. |
Мотивация и подведение учащихся к новому.
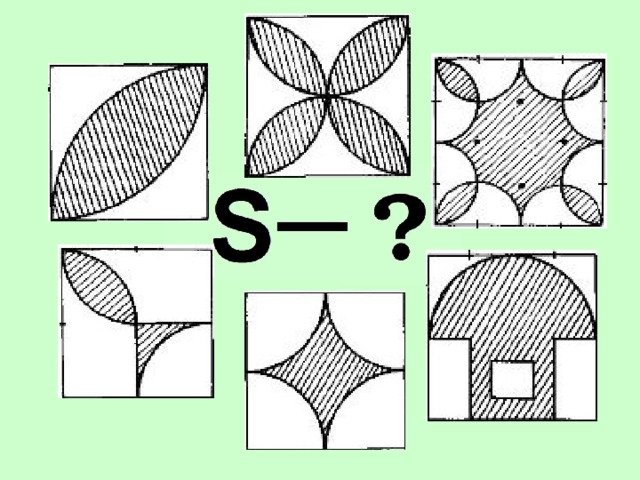
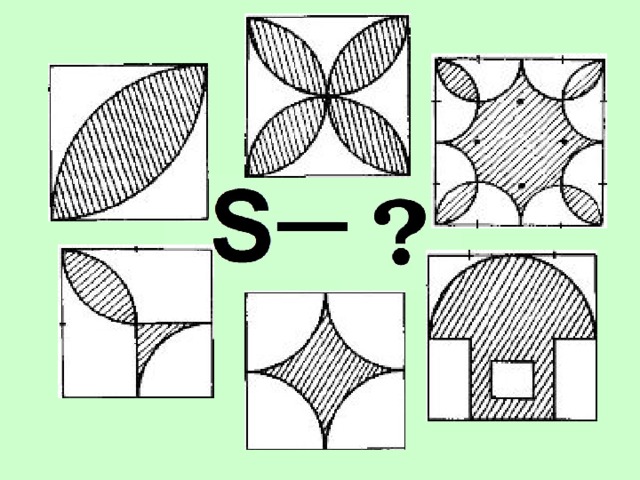
Учащимся представляется слайд и организуется обсуждение его изображений.

| Деятельность учителя | Деятельность ученика |
| Как вы думаете, как можно найти площадь таких фигур? | Дети затрудняются ответить. |
| Присмотритесь, пожалуйста, какие фигуры или части фигур вы здесь видите? | Дети с помощью учителя замечают, что данные фигуры состоят из частей круга. |
| А надо ли нам находить такие площади? Где они могут встретиться? | Ученики отвечают. В строительстве, архитектуре, в узорах паркета, линолеума. |
Сегодня мы повторим то, что вы изучали в 6 классе – это площадь круга, а также научимся находить площади его частей. И на основе изученных формул, мы сможем найти площади сложных фигур, которые мы сейчас видим или которые встречаются в окружающем мире.
Введение нового.
Для начала мы изучим главные определения понятий данной темы, без которых будет гораздо труднее, и повторим уже известные. (Представляется слайд и организуется работа по вопросам и заданиям учителя.)
| Деятельность учителя | Деятельность ученика |
| Какая фигура называется кругом? Начертите в тетради круг. | Ученики отвечают без затруднений, т. к. этот вопрос уже звучал. Чертят в тетради фигуру. |
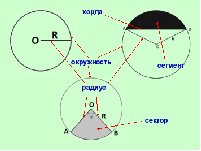
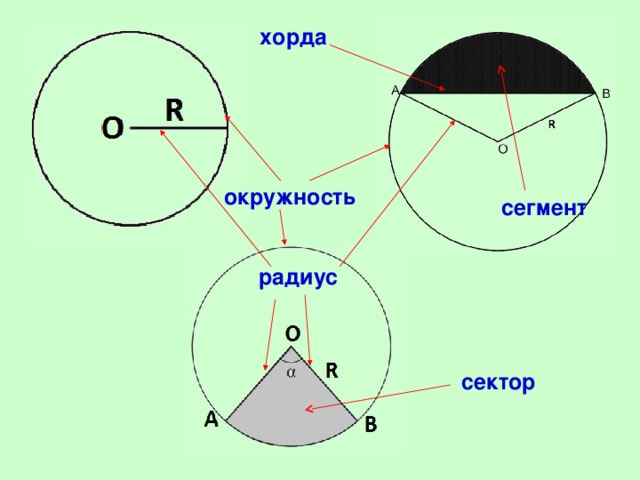
| Какие элементы круга вы знаете? Давайте посмотрим на слайд. |
| Какая фигура называется окружностью? | Окружность – геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки плоскости. |
| Что такое радиус? Назовите радиусы на данном слайде. | Радиус – отрезок, соединяющий точку окружности с ее центром. |
| Какой отрезок называется хордой? Диаметр является хордой? Назовите хорду, изображенную на рисунке. | Хорда – отрезок, соединяющий две точки окружности. |
| Какая фигура называется круговым сектором? Нарисуйте в тетради сектор, угол которого больше 180 градусов (меньше 180). | Учитель помогает ученикам ответить на данный вопрос, просит учеников привести примеры таких фигур из жизни. |
| Какая фигура называется сегментом? Нарисуйте в тетради сегмент. Есть ли на слайде сегмент? |
Учитель формулирует и просит записать в тетрадь следующие определения: круг, круговой сектор, сегмент.

Для продолжения введения нового предлагается вспомнить некоторые факты.
| Деятельность учителя | Деятельность ученика |
| Какую формулу для нахождения площади правильного многоугольника мы знаем? | Ученики отвечают на данный вопрос, который был изучен на предыдущих уроках. 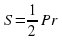 |
| В данной формуле, что означает буква P? r? | P – периметр правильного многоугольника, r – радиус вписанной окружности. |
| Чему равен радиус вписанной в него окружности? | 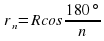
|
| Чему равна длина окружности? | 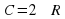
|
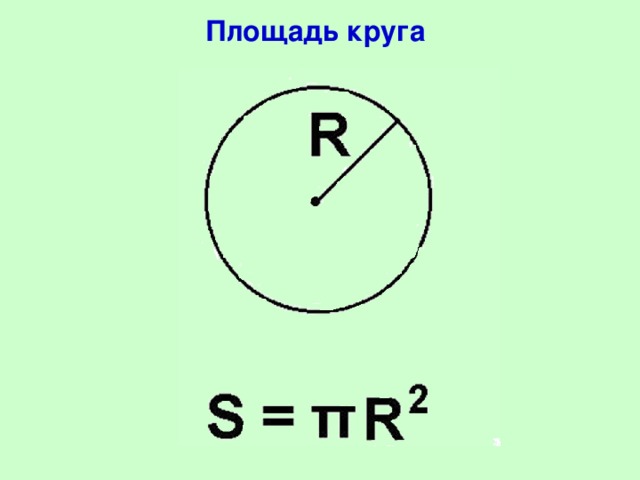
С 6 класса мы знаем, что площадь круга находится по формуле πR2, давайте теперь посмотрим, откуда взялась данная формула. Для этого будем пользоваться следующим планом:

Учитель предлагает вместе посмотреть на вывод формулы нахождения площади круга. Постоянно акцентирует внимание на непонятных частях, объясняя их детям.
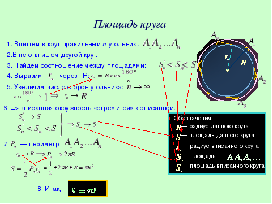
| Деятельность учителя | Деятельность ученика |
| Впишем в круг правильный n-угольник. Обратим внимание на обозначения. | Дети чертят в тетради круг и вписывают в него многоугольник. R – радиус круга, S – его площадь Sn – площадь многоугольника. |
| В него впишем другой круг. Обратим внимание на обозначения. | Дети чертят в тетради. rn – радиус данного круга, S'n – его площадь. |
| Найдем теперь закономерность между площадями. Какая площадь будет наименьшей? А наибольшей? | 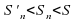
|
| Вспомним, как найти радиус вписанной в правильный многоугольник окружности? | 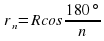
|
| Теперь будем увеличивать число сторон А1А2…Аn, т. е. n→∞. Рассмотрим 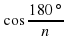 . 180 делим на очень большое число, вследствие чего получаем очень маленькое. К чему будет стремиться cos? . 180 делим на очень большое число, вследствие чего получаем очень маленькое. К чему будет стремиться cos? | 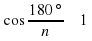
|
| А если подставить данные значения в формулу rn, что мы получим? К чему будет стремиться rn? | rn→R |
| А если радиусы вписанной и описанной окружностей становится почти равными, что будет с окружностями? | Вписанная окружность будет стремиться к описанной. |
| На данной основе делаем вывод. | 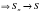  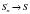
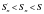
|
| Если радиусы будут равны, то чему тогда будет равен периметр правильного многоугольника при увеличении количества его сторон? | 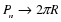
|
| Теперь из условия, что Sn→S найдем площадь круга S. | 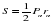
|
| Подставим известные значения в формулу и получим искомую формулу. | 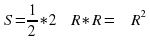
|
| Учитель предлагает ученикам задать вопросы по данному выводу. | Ученики задают вопросы. |
| Слайд №12. Учитель предлагает записать формулу нахождения площади круга. | Ученики записывают |
| Сколько параметров содержит данная формула? | Данная формула содержит два параметра: S, R. |
| Сколько типов задач на данную формулу можно придумать? | На данную формулу можно придумать 2 типа задач. Нахождение радиуса, когда известна S, и нахождение S, когда известен R. |
| Учитель предлагает ученикам сформулировать и решить задание из учебника №1114. | Ученики формулируют и устно решают. |
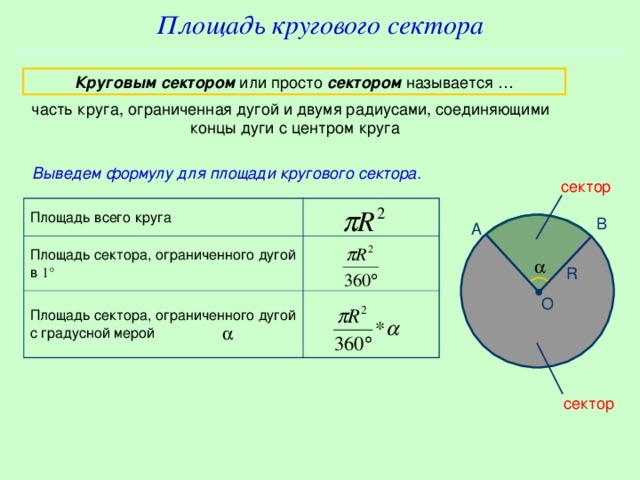
| Учитель предлагает вспомнить определения сектора. | Сектор – часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. |
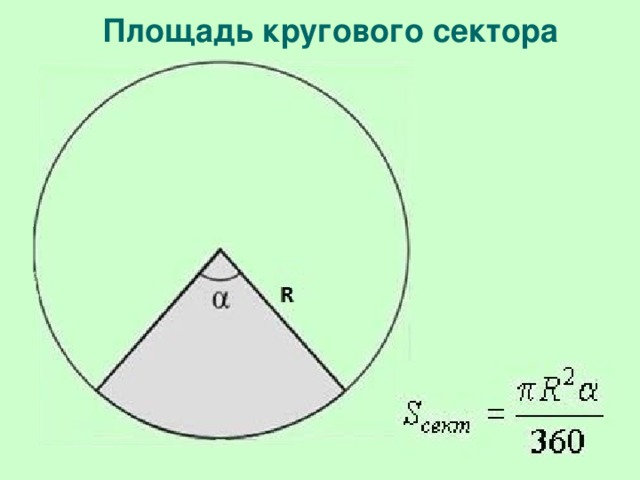
| Слайд №13,14. Учитель вместе с учащимися выводит формулу площади кругового сектора. | Ученики справляются с данным заданием, т. к. оно проводится поэтапно. Записывают формулу. |
| Сколько параметров содержит данная формула? | Данная формула содержит три параметра: S, R, α. |
| Сколько типов задач на данную формулу можно придумать? | На данную формулу можно придумать 3 типа задач. Нахождение радиуса, когда известна S и α, нахождение S, когда известен R и α, нахождение α, если известны S и R. |
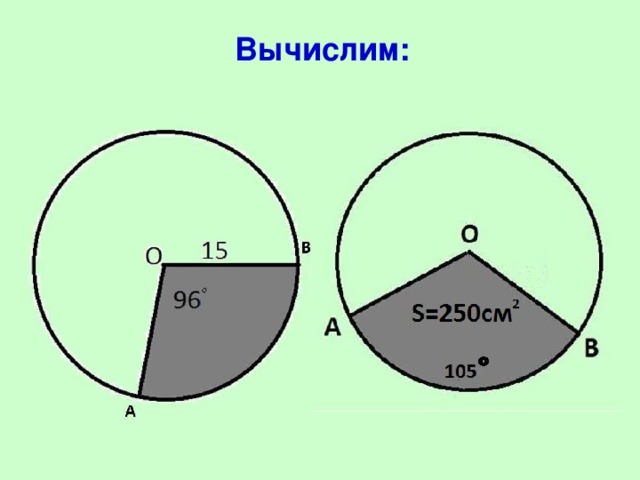
| Учитель предлагает ученикам сформулировать и решить задачи, показанные на слайде №15. | Ученики формулируют и устно решают. |
| Учитель предлагает ученикам самостоятельно вывести формулу для нахождения площади сегмента. | Ученики самостоятельно в тетради выполняют это задание. Двое выполняют возле доски для двух случаев. После выполнения задания, дети записывают формулу в тетрадь. |
| Учитель предлагает ученикам сформулировать и решить задачи, показанные на слайде №17. | Ученики формулируют и устно решают. |

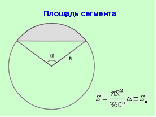
Слайд №15 Слайд №17
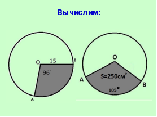
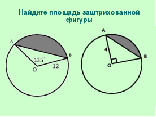
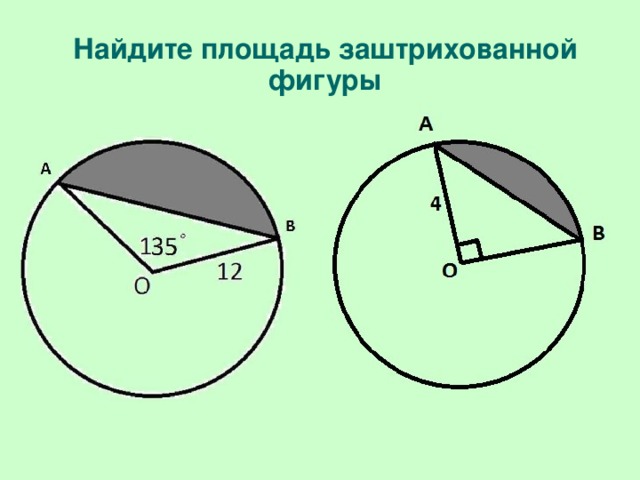
Закрепление изученного материала.
Для закрепления изученного материала предлагается найти площадь какой-либо из фигур, представленной на слайде. Пусть сторона квадрата равна 4.
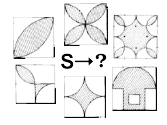
Подведение итогов.
| Деятельность учителя | Деятельность ученика |
| Что мы изучали сегодня на уроке? | Ученики отвечают на поставленный вопрос. На уроке мы изучали площадь круга и его частей. |
| Значима ли для нас данная тема? | Здесь все дети ответят «Да». |
| Где мы можем ее применить? | Дети отвечают на вопрос. |
Учитель дает домашнее задание на листочках.
Пункт 111, 112.
Диаметр опалённой площади тайги от взрыва Тунгусского метеорита равен примерно 38 км. Какая площадь тайги пострадала от метеорита?
Древнегреческий математик Архимед установил, что длина окружности относится к длине диаметра примерно как 22: 7. Найдите площадь круга, если длина диаметра 4,2 дм.
Найти площадь кольца, если r1=2,5см, r2=1,5см.





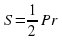
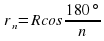


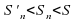
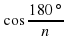 . 180 делим на очень большое число, вследствие чего получаем очень маленькое. К чему будет стремиться cos?
. 180 делим на очень большое число, вследствие чего получаем очень маленькое. К чему будет стремиться cos?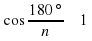
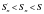
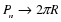
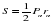
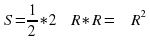













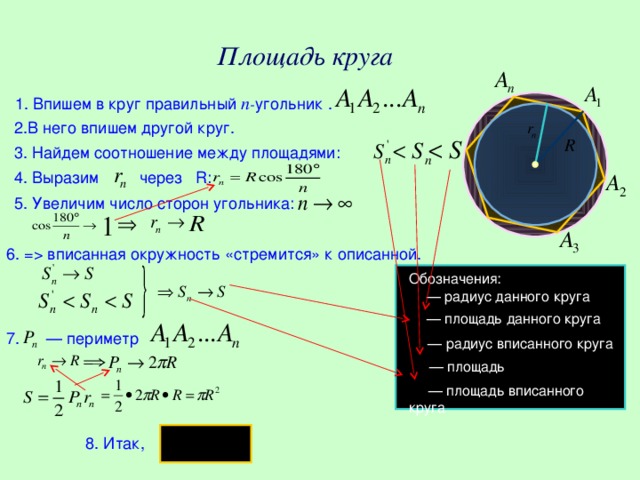 вписанная окружность «стремится» к описанной. Обозначения: — радиус данного круга — площадь данного круга 7. — периметр — радиус вписанного круга — площадь — площадь вписанного круга 8. Итак," width="640"
вписанная окружность «стремится» к описанной. Обозначения: — радиус данного круга — площадь данного круга 7. — периметр — радиус вписанного круга — площадь — площадь вписанного круга 8. Итак," width="640"