Цели и задачи: обобщение и систематизация знаний учащихся; закрепление основных понятий базового уровня.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок по алгебре и начала анализа в 11 классе "Интеграл"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок по алгебре и начала анализа в 11 классе "Интеграл"»
Полезное для учителя
Распродажа видеоуроков!
1790 руб.
2560 руб.
2000 руб.
2860 руб.
2220 руб.
3170 руб.
2100 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




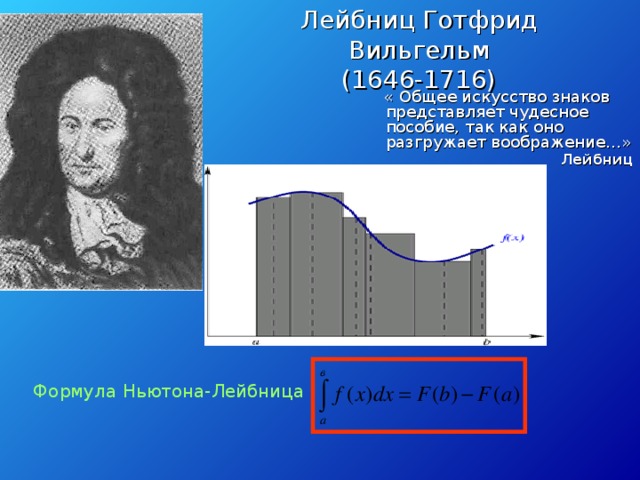
 ∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до в и обозначают 5.Официальной датой рождения дифференциального исчисления можно считать май 1684, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…». Эта статья в сжатой и малодоступной форме излагала принципы нового метода, названного дифференциальным исчислением." width="640"
∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до в и обозначают 5.Официальной датой рождения дифференциального исчисления можно считать май 1684, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…». Эта статья в сжатой и малодоступной форме излагала принципы нового метода, названного дифференциальным исчислением." width="640"