Урок по алгебре 7 класса "Взаимное расположение прямых на плоскости"

Архив RAR содержит описание урока, презентацию к уроку, 3 задания в таблице Excel.

Урок изучения нового материала. Используется групповая форма работы, фронтальный опрос, индивидуальная работа. Цель: изучить, от чего зависит взаимное расположение прямых на плоскости, выработать умение определять взаимное расположение прямых на плоскости; создать условия для развитиямышления учащихся; воспитывать желание расширять кругозор. Оборудование: компьютер, медиапроектор, карточки.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«урок»

Тема урока: Взаимное расположение графиков линейных функций.

Тип урока: Изучение нового материала.

Класс: 7

Учитель: Кизилова Федосья Артамоновна, учитель математики МОУ Койской ООШ Партизанского района

Программа: Математика 5 – 11 кл./ Сост.Г.М.Кузнецова, Н.Г.Миндюк.

Учебник: А.Г.Мордкович, М.: Мнемозина, 2009. Учебник «Алгебра – 7»

Технология: Групповая, с элементами педагогической мастерской.

Цели урока:

образовательные:

изучить, от чего зависит взаимное расположение графиков линейных функций;

выработать умение определять расположение графиков линейных функций.

развивающие:

создать условия для развития мышления учащихся; развивать наблюдательность;
способствовать развитию умения самостоятельной работы с ПК.

воспитательные:

воспитывать желание расширять кругозор,
соблюдать учебную дисциплину,
проявлять коммуникабельность, желание сотрудничать.

Тип урока: комбинированный урок изучения нового материала.

Формы: Фронтальный опрос, индивидуальная работа, групповая работа,.

Оборудование:

медиапроектор,
компьютеры,
презентация
программа Excel

Структура урока:

Организационный момент. (1 мин.)
Введение в тему. Постановка учебных задач.(2 мин.)
Исследовательская работа (10 мин.)
Физкультминутка. (1 мин.)
Закрепление изученного материала. (10мин.)
Творческая работа (10 мин.)
Рефлексия. (2-3 мин.)
Домашнее задание. (1-2 мин.)

Организационный момент.
Введение в тему. Постановка учебных задач.

Прочитайте тему нашего урока.

1). Какая функция называется линейной?

2. Выберите уравнения, которые задают линейную функцию:

а) у=-17,4х + 2 д) у =

б) у = 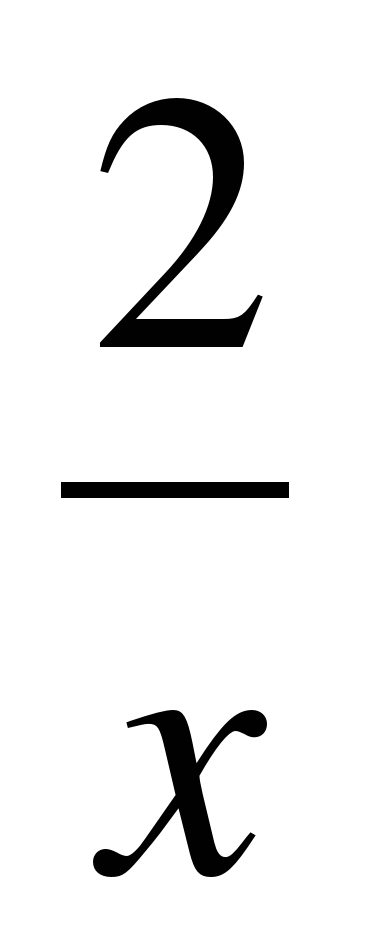е) у = 13,2х

в) у = 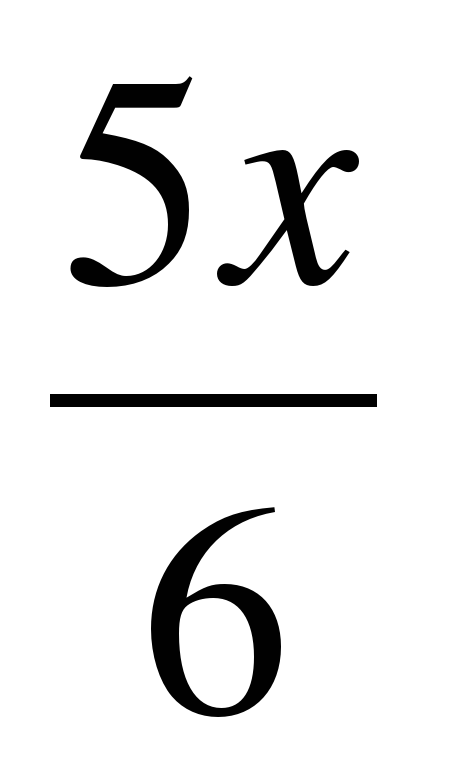ж) у = х

г) у = 2 – х з) у = 1,8-4х

2) Как называется переменная х и у в уравнении линейной функции?

3) Что показывает коэффициент k? m?

5) Что является графиком линейной функции?

6) Как вы понимаете фразу «взаимное расположение» прямых, сколько прямых для этого необходимо?

7) Как могут располагаться прямые?

8) Значит, чему вы на уроке должны научиться?

(Изучить, от чего зависит взаимное расположение графиков линейных функций; выработать умение определять расположение графиков линейных функций).

Итак, мы уже умеем строить графики линейных функций, знаем их особенности, связанные с различными коэффициентами, но каждый раз мы имели дело с одной линейной функцией. В жизни же нас окружает множество прямых и очень важно по записи функций определять их взаимное расположение. Именно изучением взаимного расположения графиков линейных функций мы и займемся на этом уроке.

3. Исследовательская работа

Перед учащимися ставится задача:

«В одной координатной плоскости построить графики функций и найти координаты точек пересечения графиков. Подтвердить значения координат аналитическим решением».

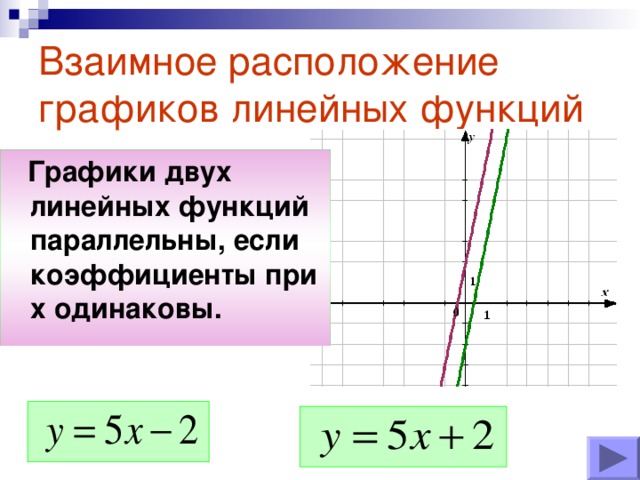
1 группа. у=5х-2; у=5х+2

1задание: Построить графики функций в тетради и найти координаты точек пересечения графиков (достаточно двух)

2 задание: Построить графики функций в программе Excel и найти координаты точек пересечения графиков.

3 задание: Найти координаты точек пересечения графиков аналитически (решить уравнения) (достаточно двух)

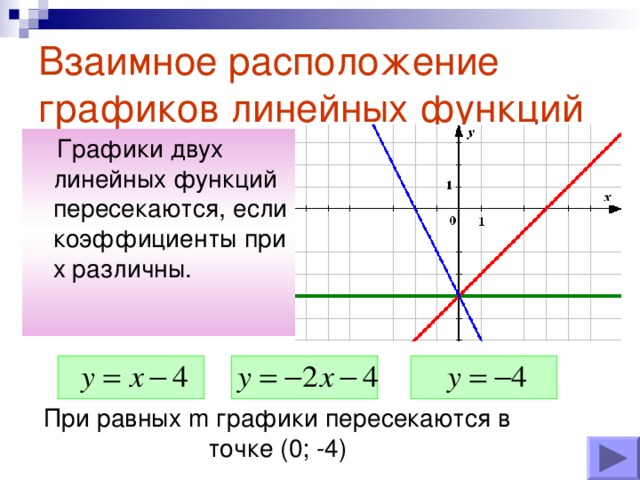
2 группа. у=х-4; у= -2х-4

2 задание: Построить графики функций в программе Excel и найти координаты точек пересечения графиков.

3 задание: Найти координаты точек пересечения графиков аналитически (решить уравнения) (достаточно двух)

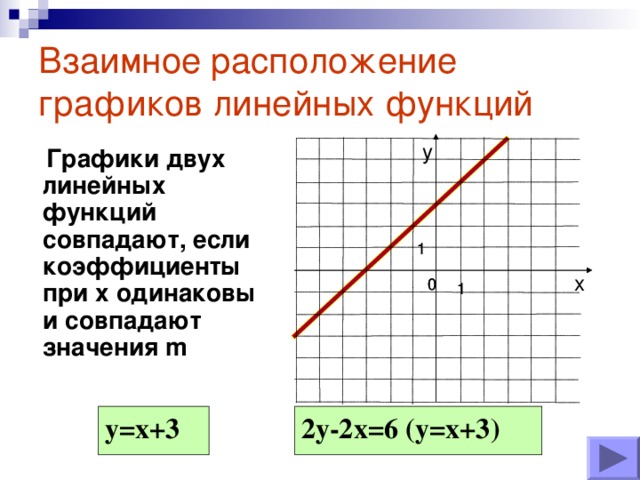
3 группа. у=х+3; 2у-2х=6

1задание: Построить графики функций в тетради и найти координаты точек пересечения графиков

2 задание: Построить графики функций в программе Excel и найти координаты точек пересечения графиков.

3 задание: Найти координаты точек пересечения графиков аналитически (решить уравнения)

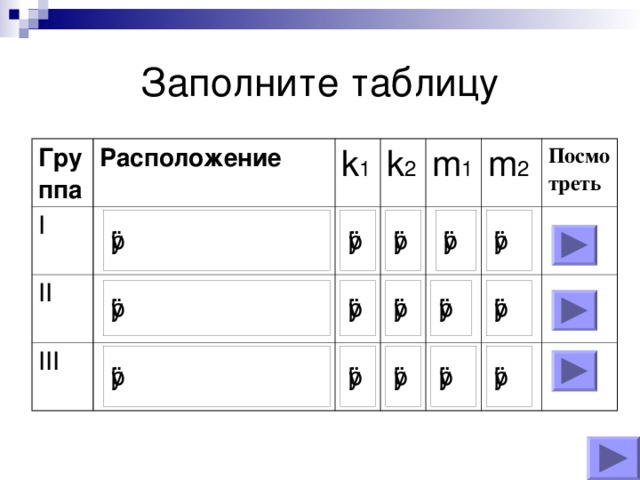
Получив результаты, учащиеся демонстрируют полученные решения в таблице презентации.

расположение	k₁	k₂	m₁	m₂
пересекаются	1	-2	-4	-4
параллельны	5	5	-2	2
совпадают	1	1	3	3

Итак, что же получилось у участников первой группы?

- прямые параллельны.

Как вы думаете, при каком условии прямые параллельны?

Обратите внимание на угловые коэффициенты.

- они равны.

Значит, признаком параллельности прямых служит равенство угловых коэффициентов, то есть k_{1 =}k_2.

А теперь послушаем участников второй группы.

- совпадают.

При каком условии прямые совпадают?

Обратите внимание на угловой коэффициент и свободный член, то есть

k_{1 =}k_2,m₁₌ m_2.

Значит, прямые совпадают, если угловые коэффициенты равны и свободные члены равны.

Слушаем участников третьей группы? Что у вас получилось?

- пересекаются.

При каком условии прямые пересекаются?

Обратите внимание на коэффициенты.

- они различны.

Значит, для того чтобы прямые пересекались, они должны иметь различные угловые коэффициенты

4. Физкультминутка.

Не поворачивая головы, посмотрите вверх – вниз – вправо – влево и закройте глаза. «Да» – вытянуть руки вверх, «нет» – вытянуть руки вперед, «не знаю» – вытянуть руки в стороны. Верны ли следующие утверждения:

Верно ли, что линейное уравнение с двумя переменными имеет бесконечно много решений?
Если две прямые пересекаются, то система линейных уравнений имеет одно решение.
Система линейных уравнений имеет бесконечно много решений, когда графики прямых параллельны.
Сегодня на уроке присутствует больше мальчиков.

Откройте глаза и быстро-быстро поморгайте. Закройте глаза. Откройте глаза. Продолжим нашу работу.

5. Закрепление изученного материала.

Определите взаимное расположение графиков функций

у=5х-3 и у=-3+5х

у=2х+1 и у=х-4

у=х+3 и у-х-3=0

у=3х-1 и у=-х-1

6. Творческая работа.

Перед вами линейная функция у = -5х -7.

Первая группа придумывает такую линейную функцию, чтобы графики этих функций пересекались.

Вторая группа придумывает такую линейную функцию чтобы, графики этих функций пересекались в точке (0;-7).

А третья группа придумывает такую линейную функцию чтобы, графики этих функций были параллельны.

Следующее задание у =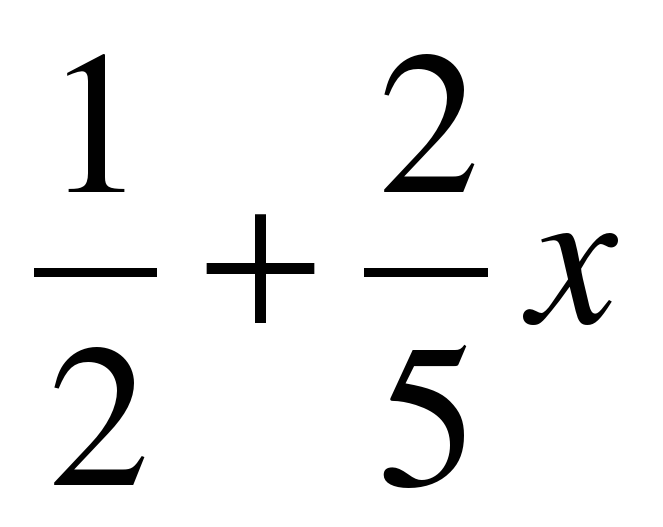

Первая группа придумывает уравнение такую линейную функцию чтобы, графики этих функций пересекались в точке (0;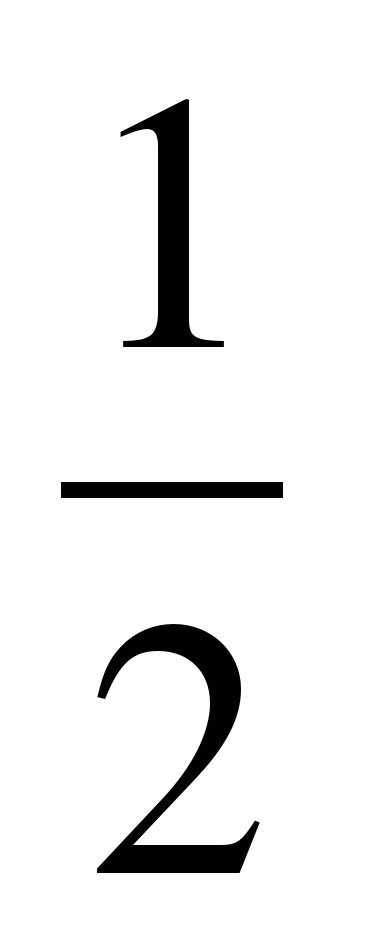). Вторая группа придумывает такую линейную функцию чтобы, графики этих функций были параллельны. А третья группа придумывает такую линейную функцию, чтобы графики этих функций пересекались

Следующее задание: у = 2 (х + 1) – 3.

Первая группа придумывает такую линейную функцию чтобы, графики этих функций были параллельны. Вторая группа придумывает такую линейную функцию, чтобы графики этих функций пересекались. А третья группа придумывает такую линейную функцию чтобы, графики этих функций пересекались в точке (0;-1).

6. Подведение итога занятия, домашнее задание

Когда графики пересекаются? Когда параллельны? Когда совпадают. Домашнее задание: № 10.10.

7. Рефлексия

И самое последнее задание: перед вами лежат карточки с вопросами, прочитайте вопросы, подумайте и ответьте. При выходе из аудитории карточки положите мне на стол. Подписывать их не надо, отвечайте абсолютно честно, мне интересно как вы восприняли это занятие, остались ли у вас сомнения, помог ли вам компьютер при работе. Думаем, отвечаем. Спасибо. Занятие закончено.

Карточка:

На каждый из вопросов можно ответить тремя способами: да, нет, частично
Понятен ли вам новый материал	Интересен ли он вам	Считаете ли вы его полезным	Помог ли вам компьютер при изучении нового материала	Чувствовали ли вы себя комфортно на занятии

Просмотр содержимого презентации
«Взаимное расположение»

Взаимное расположение графиков линейных функций

Выберите уравнения, которые задают линейную функцию:

у=

у=-17,4х+2

у=х

у=

у=1,8-4х

у=2-х

у=3,2х

Подумай!

Верно

Подумай!

Верно

у=

Верно

Взаимное расположение графиков линейных функций

Чему вы должны научиться на уроке?

Цель урока

Изучить, от чего зависит взаимное расположение графиков линейных функций;
выработать умение определять расположение графиков линейных функций

Практическая работа

Задания группам

1задание: Построить графики функций в тетради и найти координаты точек пересечения графиков.
2 задание: Построить графики функций в программе Excel и найти координаты точек пересечения графиков.
3 задание: Найти координаты точек пересечения графиков аналитически (решить уравнения).

( I группа: у=5х-2 и у=5х+2); ( II группа: у=х-4 и у=-2х-4); ( III группа: у=х+3 и 2 у-2х=6)