Теорема синусов.
Цель урока: формулирование и доказательство теоремы синусов; применение ее при решении задач.
Задачи:
образовательная
- познакомить с формулировкой и доказательством теоремы синусов;
- выработать у учащегося навыки решения задач с использованием тригонометрических функций;
развивающая:
- развитие внимания, мышления, наблюдательности, активности;
- развитие устной и письменной речи;
воспитательная:
- воспитание интереса к предмету математики.
Ход урока
1. организационный момент.
Здравствуйте, я рада вас видеть.
Чем мы занимались на прошлом уроке? (мы доказали теорему о площади треугольника)
Сегодня на уроке мы продолжим работать с треугольником и расширим свои знания о нем.
Я уверена, что на этом уроке мы с вами будем так же дружно и успешно работать, как и на предыдущих занятиях.
Желаю вам новых открытий и успешных ответов.
2. Актуализация знаний.
Сформулируйте теорему о площади треугольника
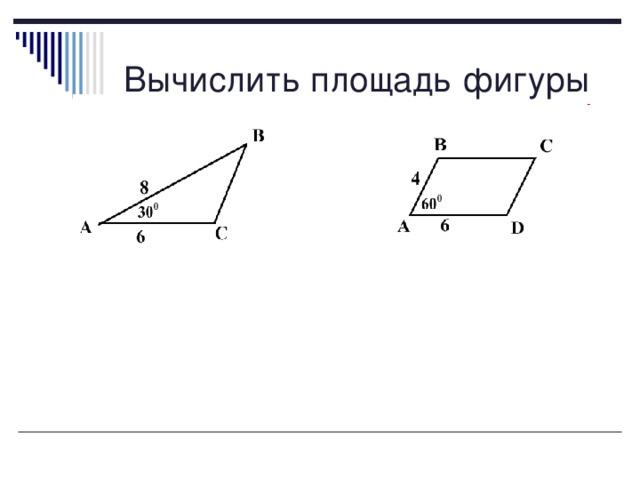
Вычислите площади фигур
Фронтальный опрос:
(повторение формул для вычисления площади треугольника).
а) формулы площади треугольника
в) определение sin, cos, tg острых углов прямоугольного треугольника.
Устные упражнения:
3. Проблемная ситуация.
1) Предлагается решить задачу (работа в группах).
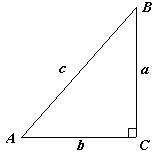
Верно ли для прямоугольного треугольника равенство:?
c=c=c
После того, как учащийся убедился, что в прямоугольном треугольнике стороны пропорциональны синусам противолежащих углов, ставится вопрос: «Верно ли это утверждение для любого треугольника?».
Что вам придется доказывать? (равенство отношений)
Как называется утверждение, которое требуется доказать? (теорема)
Сформулируйте тему урока. (Доказать теорему о том, что отношения сторон к синусам противолежащих углов равны)
В геометрии эта теорема называется теоремой синусов.
Согласованная тема записывается на доске и в тетрадях
«Теорема синусов».
4. Объяснение нового материала.
Сформулируйте теорему на основе выводов из решения задачи.
Доказательство теоремы.
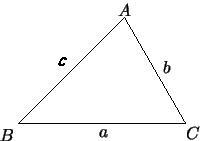
1) Теорема: Стороны треугольника пропорциональны синусам противолежащих углов.
Дано: Пусть в AB = c, BC = a, AC = b.
Доказать: .
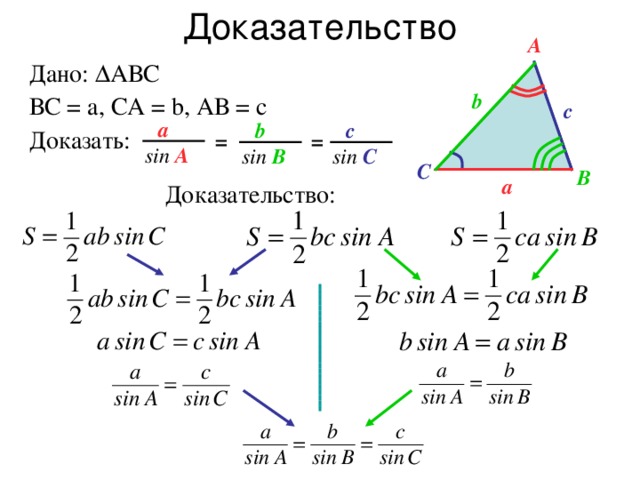
Доказательство.
По теореме о площади треугольника
Из первых двух равенств получаем значит, аналогично, из второго и третьего равенств следует Итак, . Теорема доказана.
Теорему можно записать и в другом виде:
А где мы можем проверить правильность нашего решения?
Откроем учебники на стр. 256.
Итак, мы доказали теорему синусов.
1) Запишите теорему синусов для треугольников:
ΔМНР:
ΔОКТ:
Физпауза.
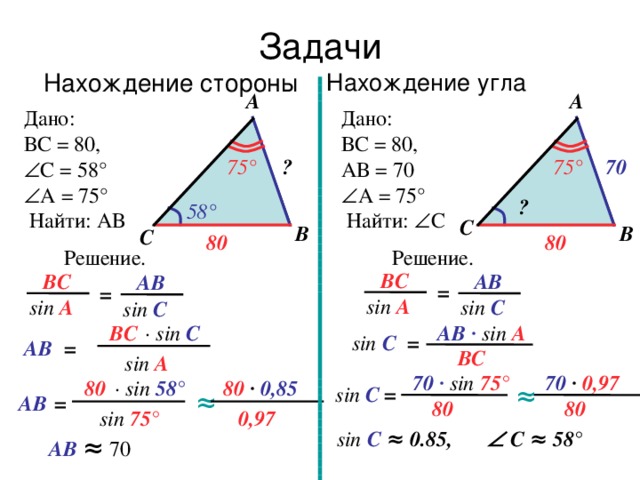
5. Закрепление материала.
Чем вы сейчас будете заниматься? (будем выполнять задание, где используется теорема синусов)
6. Замечание
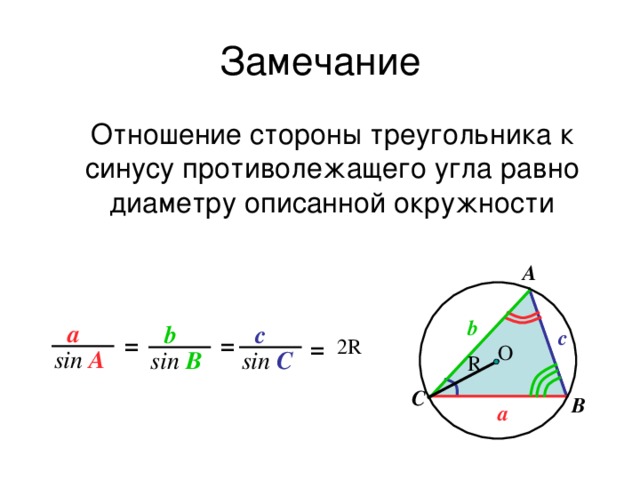
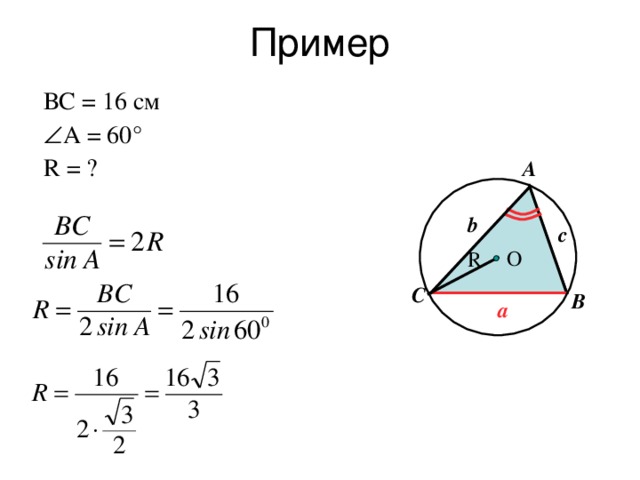
В теореме синусов в том виде, в каком мы ее получили, присутствует недоговоренность: мы узнали, что отношения сторон к синусам противолежащих им углов равны между собой, но чему же именно равны эти отношения? Чтобы ответить на этот вопрос, обратимся к задаче №1033.
Вывод: если в треугольнике против сторон a, b, c лежат углы α, β, γ соответственно, то .
где R – радиус окружности, описанной около треугольника.
Таким образом, мы получили дополнительное правило отыскания радиуса описанной около треугольника окружности.
7. Рефлексия учебной деятельности на уроке.
Какую цель вы ставили перед собой на уроке?
Вы достигли поставленной цели?
Что помогало выполнять задание?
Проанализируйте свою работу на уроке.
8. Подведение итогов.
9. Домашнее задание.
Опорный конспект; №1025 (г), №1026.
?
AB = c, BC = a, AC = b.
значит, 
аналогично, из второго и третьего равенств следует 
Итак, 
.
