Урок математики во 2 классе на тему: Площадь прямоугольника. Вывод формулы.

Конспект и технологическая карта урока.

Учебный предмет: математика.

Класс: 2.

Учитель: Сычёва Татьяна Анатольевна.

УМК: Перспектива. Автор - Петерсон Л.Г.

Тема урока: Площадь прямоугольника. Вывод формулы.

Тип урока: Изучение нового материала.

Оборудование: интерактивная доска, раздаточный материал – 2 прямоугольника на каждой парте, учебник, тетрадь, линейка.

Цель: создание условий для формирования у детей умения находить пло-

щадь прямоугольника по формуле S=a*b.

Планируемые результаты:

Предметные:

• Закрепить смысл умножения;

• Познакомить с термином «формула»;

• Вычислять площадь прямоугольника по формуле;

• Решать задачи на нахождение площади;

• Развивать математически грамотную речь.

Метапредметные:

Познавательные

• Учить сравнивать, анализировать, обобщать, делать вывод;

• Учить переводить информацию в знаково-символическую систему;

Регулятивные

• Определять и формулировать с помощью учителя цель урока;

• Планировать свои действия в соответствии с поставленной целью;

• Оценивать достигнутые результаты и причины ошибок.

Коммуникативные

• Уметь слушать и понимать речь других;

• Оформлять свои мысли в устной форме и аргументировать свою точку

зрения.

Личностные:

• Развивать навыки сотрудничества со сверстниками – работа в паре;

• Развивать чувство доброжелательности к окружающим.

Урок математики.

Тема «Площадь прямоугольника. Вывод формулы».

2 класс. УМК «Перспектива».

Учебник Петерсон Л.Г.

1.Организационный момент.

2. Этап мотивации учебной деятельности.

Уч. Сегодня урок математики нам поможет провести герой книги Марка Твена – весёлый, находчивый, любознательный, фантазёр и выдумщик, любитель приключений. Кто это?

Д. Том Сойер. (Слайд 1)

3. Этап определения темы урока.

Уч. Ребята нашего класса прочитают диалог из этого произведения. Ваша

задача – определить тему урока, исходя из сюжета.

(Текст диалога:

Автор. Том появился на перекрёстке с ведром краски и длинной кистью в

руках. Он оглядел забор, и всякая радость отлетела от него, а дух погрузился

в глубочайшую тоску.

Том. Вот это да! Пять метров деревянного забора в два метра высоты. Какую же площадь мне надо покрасить?

Автор. Вздыхая, он окунул кисть в ведро и провёл ею по верхней доске забо-

ра, повторил эту операцию, проделал её снова, сравнил ничтожно выкрашен-

ный квадрат с необозримым материком забора и уселся под дерево в полном

унынии.

Том. Если я покрасил квадрат забора, какую же площадь мне осталось покра-

сить?)

Д. Площадь прямоугольника. (На доске – распечатка «Площадь прямоугольника») (Слайд 2)

4. Этап целеполагания.

Уч. Чему будем учиться на уроке?

Д. Находить площадь прямоугольника.

Уч. Мы выведем формулу нахождения площади прямоугольника.

Какие знания нам нужны будут на уроке?

Д. Знания о прямоугольнике, что такое «плошадь прямоугольника», единицы

площади.

5. Этап повторения и подготовки к изучению нового материала.

(Слайды 3, 4, 5)

Дети вспоминают, что такое прямоугольник, его отличительные признаки, единицы измерения площади.

Физминутка.

6. Этап актуализации и фиксации затруднения. Практическая работа.

У детей на партах лежат прямоугольники – синий (со сторонами 6 см и 4 см) и красный (со сторонами 8 см и 3 см).

Уч. Сравните площади этих прямоугольников, не измеряя их.

( Предположения детей фиксируются на доске).

Возникает проблемная ситуация – одни дети говорят, что площадь прямоугольников одинаковая, другие – разная.

Уч. Что надо сделать, чтобы дать точный ответ?

Д. Измерить стороны и вычислить площадь прямоугольников.

Уч. Синий прямоугольник будут измерять и чертить в тетради – мальчики, а красный – девочки. (Дети работают самостоятельно).

Работа в парах.

Уч. Что надо делать дальше?

Д. Разделить прямоугольник на квадратные см и посчитать их.

7.Этап открытия нового знания.

Проверка самостоятельной работы мальчиков и девочек.

Уч. Сколько полос с квадратами получилось?

Сколько квадратов в каждой полосе?

Как узнать, сколько всего квадратов?

Как это выражение можно записать короче?

Д. Заменить его выражением на умножение.

(Слайд 6)

Уч. Как называется сторона прямоугольника 6 см и 8 см? А сторона 4 см и 3 см?

Сделайте вывод, как найти плошадь прямоугольника. (Слайды 7, 8).

Уч. Запишите формулу в тетрадь.

Откройте учебник на с.73, прочитайте правило и сравните его с тем, которое мы вывели на уроке.

Необходимость нового знания.

Уч. Где и когда в вашей жизни может возникнуть необходимость вычислять площадь прямоугольника?

Дети прогнозируют такие ситуации.

8. Этап включения нового знания в систему знаний.

Уч. Теперь пришла пора помочь Тому Сойеру ответить на вопрос: «Какую же площадь забора ему осталось покрасить?».

Вспомните, что мы уже знаем?

Д. Длина забора – 5 м, высота – 2 м. Он уже покрасил 1 кв.м забора.

Уч. моделирует условие задачи на интерактивной доске, чтобы дети могли наглядно увидеть и понять ход её решения.

- Что известно по условию?

- Что надо найти?

- Сможем ли мы сразу ответить на вопрос задачи? Почему?

- Как будем узнавать площадь всего забора?

(Учитель записывает решение на доске, а дети – в тетрадях).

- Как узнать площадь не закрашенной части забора?

- Ответили ли мы на вопрос задачи?

- Запишите ответ задачи.

9. Рефлексивно-оценочный этап.

Уч. Какую задачу ставили перед собой на уроке?

Удалось ли решить её?

Кто считает, что после этого урока может самостоятельно находить площадь прямоугольника? ( Детям выдаётся тест для выполнения дома по желанию)

Кому было интересно сегодня на уроке? Какому смайлику соответствует ваше настроение? (Рефлексивный слайд).

10. Домашнее задание. Слайд 9 – распечатать и дать детям для домашнего

выполнения по желанию. Задание, обязательное для всех, учитель берёт из

учебника на своё усмотрение.

Технологическая карта урока математики во 2 классе по теме «Площадь прямоугольника. Вывод формулы».

ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА

1

2

4

6

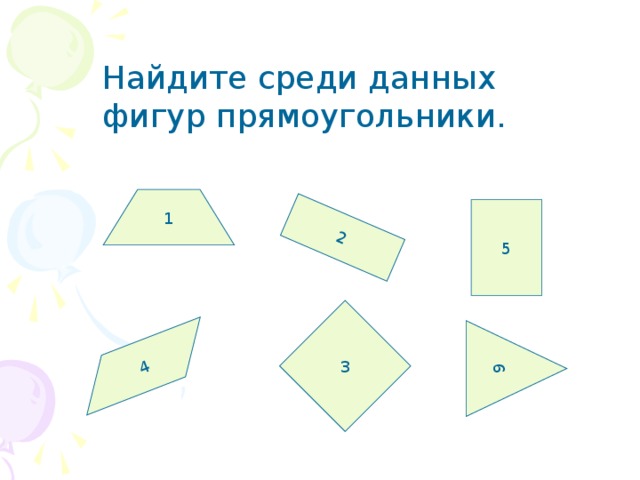
Найдите среди данных фигур прямоугольники.

5

3

2

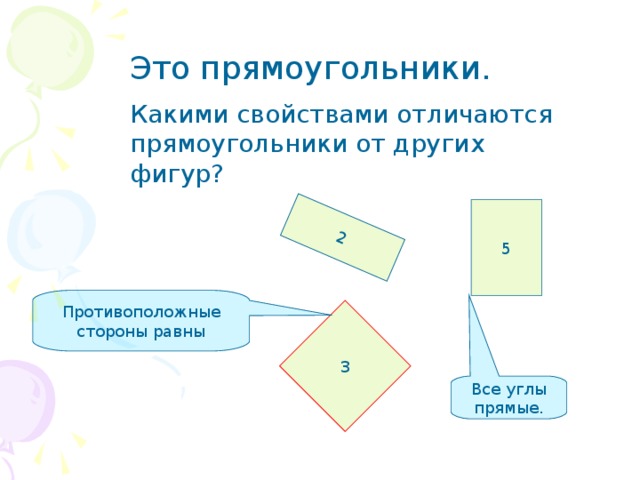
Противоположные стороны равны

Это прямоугольники.

Какими свойствами отличаются прямоугольники от других фигур?

5

3

Все углы прямые.

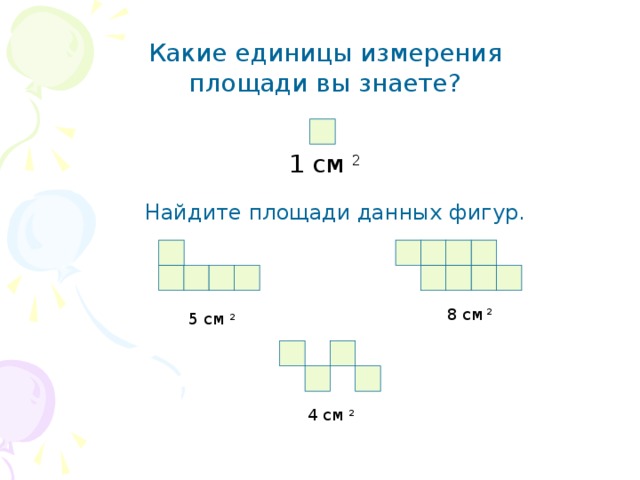
Какие единицы измерения площади вы знаете?

1 см 2

Найдите площади данных фигур.

8 см 2

5 см 2

4 см 2

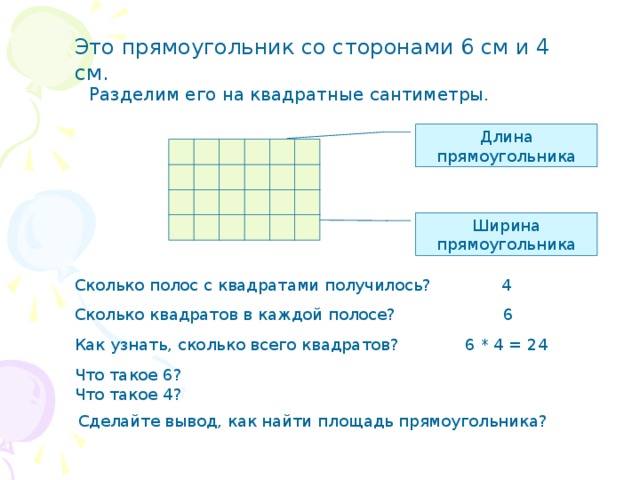
Это прямоугольник со сторонами 6 см и 4 см.

Разделим его на квадратные сантиметры.

Длина прямоугольника

Ширина прямоугольника

Сколько полос с квадратами получилось?

4

Сколько квадратов в каждой полосе?

6

Как узнать, сколько всего квадратов?

6 * 4 = 24

Что такое 6?

Что такое 4?

Сделайте вывод, как найти площадь прямоугольника?

Площадь прямоугольника

• Чтобы найти площадь прямоугольника, измеряют его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел.
• Чтобы найти площадь прямоугольника, надо его длину умножить на ширину.

Существует формула вычисления площади прямоугольника.

S пр = a * b,

где a – длина прямоугольника,

b – ширина.

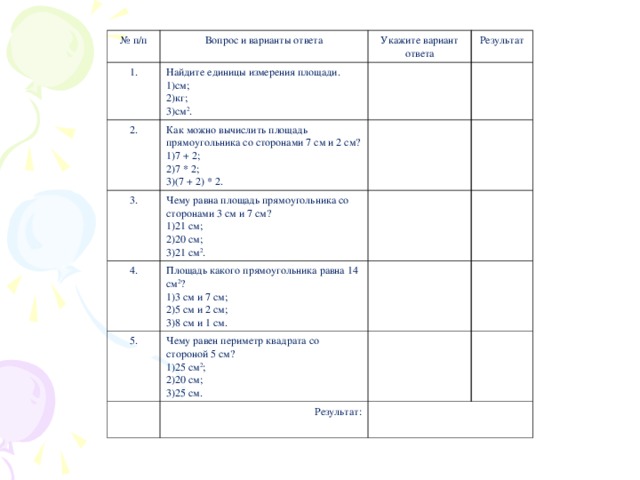
№ п/п

Вопрос и варианты ответа

1.

Укажите вариант ответа

2.

Найдите единицы измерения площади.

Результат

Как можно вычислить площадь прямоугольника со сторонами 7 см и 2 см?

3.

• см;
• кг;
• см 2 .

• 7 + 2;
• 7 * 2;
• (7 + 2) * 2.

Чему равна площадь прямоугольника со сторонами 3 см и 7 см?

4.

• 21 см;
• 20 см;
• 21 см 2 .

Площадь какого прямоугольника равна 14 см 2 ?

5.

• 3 см и 7 см;
• 5 см и 2 см;
• 8 см и 1 см.

Чему равен периметр квадрата со стороной 5 см?

• 25 см 2 ;
• 20 см;
• 25 см.

Результат: