Тема урока: Рациональные числа.
Цели урока:
Создать условия, при которых ученик:
- расширит представления о числе, сформирует понятие «рациональное число»;
- систематизирует знания о числовых множествах;
- приобретет навыки перевода рациональных чисел в десятичную (конечную или бесконечную) дробь; бесконечных десятичных периодических дробей в рациональные числа; различные способы перевода бесконечной десятичной периодической дроби в обыкновенную дробь;
- приобретет умения работать в парах,
- разовьет навыки самостоятельной работы, умения анализировать, сравнивать, внимательно выполнять необходимые действия.
В результате ученик:
- знает, как определить вид числа, его принадлежность к числовым множествам;
- умеет правильно пользоваться математической символикой в процессе выполнения заданий;
- умеет представлять рациональное число в виде конечной или бесконечной периодической дроби;
- сможет научиться представлять бесконечную периодическую дробь в виде обыкновенной дроби;
Ход урока:
- Организационный этап. Повторение изученного.
- Устный счет (слайд 2).
- Верно ли…
- что число -5 - натуральное?
- что натуральные числа использовали для счета предметов?
- что самое маленькое натуральное число – это 0?
- что любое натуральное число (например, 4) можно записать в виде обыкновенной дроби?
- что дроби появились, когда люди стали делить между собой имущество, измерять земельные участки, исчислять время?
- что - это натуральное число?
- что любое целое число (например, -67) можно записать в виде десятичной дроби?
- что знак Î означает «принадлежит»?
- что запись «(3;5) Ì (2;9)» означает «промежуток от 3 до пяти является частью промежутка от 2 до 9»?
- что утверждение «2 Ï Z» - верное?
- что -7 > 0?
- что знак Ë означает «является частью»?
- что - это дробь?
- что множество целых чисел – самое маленькое?
- Основной этап урока с сообщение нового блока теории и проверки имеющихся знаний.
Давайте вспомним, какие числа на сегодняшний день мы с вами знаем:
- Натуральные числа – N (слайд 3)
- Для того чтобы вычитание натуральных чисел было выполнимо во всех случаях, множество натуральных чисел дополняют числом 0 и числами, противоположными натуральным и все вместе они составляют множество целых чисел – Z (слайд 4)
- Обыкновенной дробью называется число вида (где m – целое число, а n – натуральное число). Например:,,, – обыкновенные дроби. (слайд 5). Число m называют числителем дроби, а число n – знаменателем дроби.
- Всякое целое число можно также рассматривать как обыкновенную дробь со знаменателем 1. Например:-7,0,5
- Напомню основное свойство дроби: если числитель и знаменатель данной дроби умножить или разделить на одно и тоже (не равное нулю) число, то получится дробь, равная данной дроби.
Пример 1.
Рассмотрим дробь . Умножив ее числитель и знаменатель на число 2. Получаем дробь. Эта дробь равна данной.
Разделим теперь числитель и знаменатель дроби на число (-3). Получаем дробь =. Эта дробь также равна данной. Итак, имеем: . Поэтому одну и ту же дробь можно представить в виде разными способами.
Обыкновенная дробь называется правильной, если
Пример 2.
а) дробь
б) дробь
в) дробь
г) дробь (-11)=11.
Неправильная дробь может быть записана в виде смешанной дроби, т.е. дроби, содержащей целую и дробную части. Например, ,
- Любую обыкновенную дробь можно записать в виде десятичной дроби, разделив «уголком» ее числитель на знаменатель.
Пример 3.
Обратить в десятичную дробь: а) .
В случае а) была получена конечная десятичная дробь: . В случае б) легко увидеть, что после выполненного деления вновь получается остаток 40, и процесс деления будет неограниченно продолжаться (отметь скобкой справа). Поэтому получаем: бесконечную периодическую десятичную дробь. При этом повторяющаяся группа цифр называется периодом. Принято период указывать в скобках:0,536 36 …=0,5(36). Читают: 0 целых 5 десятых и 36 в периоде.
Учитывая, что конечная десятичная дробь не измениться, если после последней цифры записать любое количество нулей (например, 0,075=0,0750=0,07500 и т.д.), конечные десятичные дроби можно рассматривать как бесконечные периодические десятичные дроби с периодом нуль (например. 0,075=0,075(0)). Однако замечу, что период нуль никогда не указывается.
Таким образом, любая обыкновенная дробь может быть представлена единственным образом в виде бесконечной периодической десятичной дроби.
Справедливо также и обратное утверждение: любая бесконечная периодическая десятичная дробь может быть представлена единственным образом в виде обыкновенной дроби .
На примере рассмотрим, как производится такое обращение.
Пример 4.
Обратить в обыкновенную дробь: а)1,6; б)1,(15).
а) сразу запишем данную дробь в виде обыкновенной и выполним сокращение: 1,6=1.
б) обозначим данное число буквой х=1,(15)=1,1515… т.к. период этой дроби содержит две цифры, то умножим число х на 10²=100 и получим 100х=115,1515…. Теперь найдем разность чисел 100х и х: 100х-х=99х=115,1515….-1,1515….=114. Для нахождения х получим уравнение: 99х=114,откуда х=.
Проверить полученные результаты очень просто: надо опять обратить полученные обыкновенные дроби в десятичные:
а) 1 б) 1
К сожалению, операции над бесконечными периодическими десятичными дробями выполнить намного сложнее. Самый простой способ решения таких задач: перевести эти дроби в обыкновенные и выполнить действия с ними.
Пример 5.
Вычислить (1,(3)-1,(6))÷0,(21)
а) х=1,(3)=1,3333….Умножим это число на 10 и получим:10х=13,3333….Тогда 10х-х=9х=13,3333….-1,3333….=12.Имеем 9х=12 и х=.
б)х=1,(6)=1,666…Умножим и это число на 10:10х=16,666….Получаем 10х-х=9х=16,666….-1,666…=15.Имеем 9х= 15 и х= .
в) х=0,(21)=0,2121…Умножим это число на 100 и получим:100х=21,2121… Тогда 100х-х=99х=21,2121….-0,2121….=21,откуда 99х=21 и х=.
Теперь запишем этот пример для полученных обыкновенных дробей:
(1.
Таким образом, получаем дробь (слайд 6-7)
В заключение сделаем основной вывод: к рациональным числам относятся: целые числа, обыкновенные дроби, конечные десятичные дроби и бесконечные десятичные дроби. Все рациональные числа можно представить в виде (где m- целое число, n – натуральное число). (слайд 8)
Множество рациональных чисел обозначают буквой Q. Заметим, что разные бесконечные десятичные периодические дроби представляют разные рациональные числа. Исключением являются дроби с периодом 9, которые считают другой записью дробей с периодом 0.
Пример 6.
а) 2,(9)=2,99….=3,00…=3;
б) 2,37(9)=2,3799…=2,3800…=2,38.
Бесконечные десятичные дроби с периодом 9 заменяют дробями с периодом 0. При обращении обыкновенной дроби в десятичную не может получиться дробь с периодом 9.
Изобразите с помощью кругов Эйлера множество рациональных чисел.
3.Задание на уроке:
- В учебнике
- На слайде 9
- Самостоятельная работа (слайд 10-11)
4. Подведение итогов:
- знаем, что все числа объединены во множество рациональных чисел;
- умеем пользоваться символикой и определять принадлежность чисел и промежутков;
- умеем любое число представлять в виде дроби, где или в виде бесконечной периодической дроби;
- получили возможность научиться переводить бесконечные периодические дроби в обыкновенные двумя способами, заметили, что второй способ трудно формулировать, но его применение ускорит получение результата) (слайд 12).
5. Рефлексия (слайд 13).
6. Выставление оценок.
7. Домашнее задание. (Задание по карточкам).

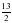 - это натуральное число?
- это натуральное число?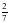 - это дробь?
- это дробь?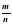 , где
, где 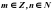 или в виде бесконечной периодической дроби;
или в виде бесконечной периодической дроби;















