Урок - игра

Известный математик Софья Васильевна Ковалевская была дочерью генерал-лейтенанта артиллерии В.В. Корвин-Круковскаго и Елены Федоровны Шуберт. Дядя ее с материнской стороны был известным математиком, а прадед еще более выдающимся астрономом.

Родилась Софья Васильевна в Москве, но детство провела в поместье "Полибино" Витебской губернии, где кроме гувернанток, с 8-летнего возраста в течение 10 лет с нею занимался их домашний наставник Малевич, приучивший ее к систематическому труду и серьезному отношению к своим обязанностям. Интерес же к математике возбудил в ней дядя ее П.В. Корвин-Круковский, который, будучи сам дилетантом в науке, благодаря своему увлечению ею, сумел заронить искру того же энтузиазма в душу 12-летней своей племянницы. Что касается пристрастия к литературе, то оно возникло у Ковалевской под влиянием сестры, удачно выступившей на этом поприще.

Ковалевская была богато одаренная натура. Она обладала, кроме выдающихся математических способностей, признанных во всей Европе и доставивших ей премии разных ученых ареопагов, еще, сверх того, литературным дарованием. Хотя призвание это проснулось в ней, к сожалению, поздно, но тем не менее, уже то, что написано ею, доказывает, что и в данном направлении у нее была искра Божия, которая, может быть, разгоралась бы в яркое пламя, если бы Софью Васильевну не подкосила преждевременная смерть. При способности к глубокому анализу, вдумчивости, тонкой наблюдательности, пылкой фантазии, Ковалевская обладала большой способностью к художественному воспроизведению виденного и перечувствованного.

Что касается научной деятельности, то раньше, чем Софья Васильевна получила доступ не только к ней, но и к изучению науки вообще, даже к простому образованию, ей пришлось устранить со своего пути не один камушек, а некоторые удары о них имели даже влияние на всю ее последующую жизнь. Одним из таких неудачных и вынужденных шагов был ее фиктивный брак с В.О. Ковалевским.

Ее отец если и не протестовал против стремления ее к знанию, то единственно только благодаря своей любви к математике и влиянию друга детства, страстного математика, открывшего необыкновенные способности у маленькой Софы: но уже одно подозрение, что дочь думает продолжать свои научные занятия, вызвало бурю, а робкий намек ее о желании уехать учиться за границу вызвал ужас.

Признаки сильной воли, проявившиеся у Ковалевской очень рано, помогли ей добиться намеченной цели и проявить на свет божий свои математические таланты, которые при других условиях, быть может, заглохли бы.

Впрочем, навряд ли одна любовь к математике и к знанию вообще могли подвигнуть Ковалевскую на такую борьбу с окружающим; в подмогу к этому явилось то просветительное движение в обществе, которое началось в 60-х годах, когда стремились учиться не только ради самого знания, сколько ради тех результатов, которые оно могло дать, подготовляя для работы на пользу Родины. Учиться, заниматься, чтобы затем с удвоенными силами служить родине, помогать ей в тяжелой освободительной борьбе с мраком и угнетением, за свободу и просвещение, во имя человеческого счастья, - вот какие стремления одушевляли тогда женскую молодежь, которая во имя этих идеалов рвала всякие путы, и с легким чемоданчиком и без всяких часто средств, стремилась в гостеприимные швейцарские университеты наперекор судьбе и обществу.

Софье Васильевне было едва 17 лет, когда она вступила в брак с Ковалевским. Проживши полгода в Петербурге, занимаясь с увлечением математикой у А.Н. Страннолюбского, об уроках которого она потом вспоминала с восторгом, молодые супруги уехали весной 1869 года в Гейдельберг, Софья Васильевна для изучения математики, а ее муж - геологии. Но и там нужно было добиваться права допущения в университет, которое и дано было Ковалевской по особому разрешению Кирхгофа.

В Гейдельберге Софья Васильевна слушала курс математики в течение двух лет. Ковалевская вскоре обратила на себя внимание своих знаменитых профессоров: Кирхгофа, Кенигсберга и других, и приобрела такую славу в небольшом Гейдельберге, что матери показывали на нее детям на улице.

В 1874 году Геттингский университет по защите Софьей Васильевной диссертации, признал ее доктором философии, а в 1881 году она была избрана в члены Московского математического общества.

После смерти мужа в 1883 году Софья Васильевна переехала с дочерью в Стокгольм, где в 1884 году получила кафедру математики в университете. Чтение лекций должно было происходить первый год по-немецки, а со второго - по-шведски. Ковалевская так скоро овладела шведским языком, что начала печатать на нем свои математические работы и даже беллетристические произведения.

Следующий ряд лет является для нее пышным триумфом, как признание ее научных заслуг и математического дарования. В 1889 году Ковалевская получила премию Стокгольмской академии наук и - в том же году, наконец и Родина оценила ее, выбрав в члены-корреспонденты Санкт-Петербургской академии наук. Что касается отношения Ковалевской к Родине, то они были самые горячие, и несмотря на то, что она жила вдали, все родное, всякий малейший успех на родине, был ей бесконечно дорог.

Несмотря на то, что Ковалевская достигла вершины человеческого счастья, она не чувствовала себя удовлетворенной, ее личная жизнь сложилась печально. В угнетенном настроении, в котором она вернулась из последней поездки заграницу, она не береглась и - простуженная и больная - продолжала ходить и читать лекции, пока окончательно не свалилась. У нее оказалось сильное воспаление легких, друзья усердно за ней ухаживали, но никто не предполагал близкого конца. Когда через несколько дней болезни се оставили одну, у нее началась агония и она умерла, покинутая всеми на руках чужой сиделки, не говорившей даже на ее родном языке. Так кончила свою жизнь великая женщина-математик Софья Васильевна Ковалевская. Хотя жизнь ее была коротка, только 41 год, но зато богата содержанием. Похоронена Софья Ковалевская в Стокгольме, где русские женщины поставили ей памятник, который был открыт летом 1896 года.

Муниципальное бюджетное общеобразовательное учреждение

«Шегарская средняя общеобразовательная школа № 2»

Сценарий урока

по математике

в 6-х классах

Тема: Координатная плоскость ПОД ДЕВИЗОМ: «УЧЕНЬЕ С УВЛЕЧЕНЬЕМ»

Составила:

Мурашкина Виктория Владимировна –

учитель математики, первая категория.

Мельниково 2014

Пояснительная записка

«Учиться можно только весело…,

чтобы переваривать знания, надо

поглощать их с аппетитом»

Анатоль Франс.

В программе математики 6 класса в главе «Рациональные числа» изучается тема «Координатная плоскость», которая является одной из основной тем всего школьного курса алгебры и геометрии. Количество часов на изучение предмета Математика всего 170 часов; в неделю: 5 ч

Актуальность: Известно, что дети среднего школьного возраста мыслят образно, наглядный материал легче ими воспринимается. Поэтому форма проведения урока-игры с элементами моделирования, где они сами делают модель ЛИСТ МЁБИУСА и узнают много нового о его применении.

Данный сценарий занятия с сопровождением презентации может быть использован как в 6 классе на уроке математики(в виде обобщающего урока по теме координатная плоскость) и также на внеклассных мероприятиях.

Цель: развитие познавательных и творческих способностей учащихся.

Задачи:

Образовательные:

овладение учащимися знаний по теме координатная плоскость;

повторение понятий и терминов математики.

Развивающие:

развитие пространственного воображения, логики и мышления;

использование математики в практической деятельности людей.

Воспитательные:

формирование интереса к предмету, развитие внимания, навыков самостоятельной работы при выполнении различных заданий на уроке.

Тип урока: обобщающий урок с элементами математического моделирования

Форма: урок – игра

Методы обучения: иллюстративно-наглядные, развивающие, проблемно-поисковые.

Форма работы: индивидуальная, работа в парах, самостоятельная работа.

Оборудование: компьютер, проектор, карточки с заданиями.

Урок проводился в 6 «а» и 6 «б» классах, использовали два кабинета. Кабинет № 1- Игровая, кабинет № 2 – Математическая мастерская. Учащиеся классов работали в каждом кабинете по 20 минут.

Учебно-методическое обеспечение:

- учебник 6 класса, автор учебника Н.Я. Виленкин;

- математика «Занятие школьного кружка», авторы О.С. Шейкина, Г.М. Сольвьева.

Время реализации занятия: 40 минут

Авторский медиапродукт создан с помощью:

1. Среда WORD

2. Power Point,

Работа учителя на уроке:

1. Постановка учебных задач.

2. Организация самостоятельной работы учащихся.

3. Консультирование учащихся в процессе самостоятельной работы.

4. Подведение итогов и оценка работы.

Описание деятельности учащихся.

1. Учащиеся работают в парах.

2. Каждая пара находит необходимую информацию по своим вопросам.

3. Учащиеся готовят сообщения с презентацией.

Ожидаемые результаты.

Учащиеся к концу урока должны уметь:

- Выполнять различные задания на координатной плоскости.

- Выполнять модель листа Мёбиуса

Знать:

- Основные математические понятия.

- Что такое лист Мёбиуса и его применение.

- Кто такая Софья Ковалевская.

Межпредметные связи на уроке.

История математики: Сведения о математиках. Геометрия.

Физика: Техническое применение листа Мёбиуса.

Технологии, используемые на уроке:

1. Игровые технологии.

2. Информационно-коммуникативные технологии.

3. Технология проблемного обучения.

4. Здоровьесберегающие технологии.

Распаковка урока по технологии

Этапы урока	Действия учителя	Действия учеников	Методы, приёмы	Полученные навыки
Первый этап	Объявление темы урока. Постановка учебных задач.	Обсуждают в парах. Высказываются по теме. Отвечают на вопросы. Первое сообщение учащихся.	Индивидуальная работа. Работа в парах.	Активизация учащихся. Обобщение и систематизация знаний. Развитие устной речи. Умение работать в паре.
Второй этап	Раздаёт раздаточный материал. Консультация учащихся	Знакомятся с технологией построения. Выполняют лист Мёбиуса	Самостоятельная работа. Моделирование	Работа с бумагой. Выполнение модели лист Мёбиуса
Третий этап	Задает вопросы для повторения темы. Проводит устное повторение, игра «Поймай рыбку»	Самостоятельная творческая работа. Отвечают на вопросы.	Игровая технология. Технология проблемного обучения.	Развитие навыка использования координатной плоскости, творческого мышления.
Четвертый этап	Раздаёт раздаточный материал.	Второе сообщение учащихся (презентация). Решаем кроссворды. Игра «Лучший художник»	Информационно-коммуникативные технологии	Развитие навыка построение координатной плоскости, творческого мышления.

Краткая характеристика 6 «А» класса

(количественная, социальная, психологическая, по уровню развития)

В классе обучаются 21 человек. Из них 7 девочек и 14 мальчиков. 2 учащихся 2001 года рождения. 2 ученика - 1998 г.р. Остальные учащиеся 2000 г.р.

Большинство учащихся дополнительно посещают спортивную школу.

Воспитывается в неполной семье 7 человек. Двое из них находятся на опекунстве.

Все ребята с разными творческими и интеллектуальными возможностями. Большинство из них – это дети со средними умственными способностями.

Трое ребят имеют диагноз «Задержка психического развития».

Четверо учащиеся обладают яркой познавательной активностью, оригинальностью психического склада.

Большинство учащихся охотно посещают школу. Они адекватны в поступках, поведении, доброжелательны в общении, участвуют в общественной жизни, принимают активное участие в конкурсах разного уровня. 2013 году учащиеся этого класса приняли участие во всероссийских соревнованиях по физической культуре в городе Анапа.

Есть в классе дети:

• повышенной активности: 4 учащихся;

• замкнутые: 2 учащихся;

• эмоционально-неуравновешанные: 2 учащихся;

• неуверенные в себе: 3 учащихся;

• не умеющие организовывать себя ни в учёбе, ни в быту: 4 учащихся.

5 ребят успешно обучаются, остальным детям не хватает усидчивости, терпения и контроля со стороны родителей.

Краткая характеристика 6 «Б» класса

(количественная, социальная, психологическая, по уровню развития)

В классе обучаются 22 человек. Из них 10 девочек и 12 мальчиков. 3 ученика - 1999 г.р. Остальные учащиеся 2000 г.р.

10 учащихся дополнительно посещают спортивные секции и 5 учащихся обучаются в музыкальной школе.

Воспитывается в неполной семье 6 человек.

Все ребята с разными способностями и интеллектуальными возможностями.

Один ученик имеет диагноз «Задержка психического развития».

Десять учащихся учатся на «4» и «5» и проявляют повышенный интерес к разным предметам.

Большинство учащихся охотно посещают школу, участвуют в общественной жизни класса, принимают активное участие в конкурсах разного уровня.

Есть в классе дети:

• повышенной активности: 3 учащихся;

• замкнутые: 4 учащихся;

• эмоционально-неуравновешанные: 2 учащихся;

• неуверенные в себе: 3 учащихся;

• не умеющие организовывать себя ни в учёбе, ни в быту: 3 учащихся.

Сценарий урока
Урок- игра по математике в 6-х классах Тема: Координатная плоскость ПОД ДЕВИЗОМ: «УЧЕНЬЕ С УВЛЕЧЕНЬЕМ»

«Учиться можно только весело…

чтобы переваривать знания, надо

поглощать их с аппетитом»

Анатоль Франс.

Цель: развитие познавательных и творческих способностей учащихся.

Задачи: Образовательные:

овладение учащимися знаний по теме координатная плоскость;

повторение понятий и терминов математики.

Развивающие:

развитие пространственного воображения, логики и мышления;

использование математики в практической деятельности людей.

Воспитательные:

формирование интереса к предмету, развитие внимания, навыков самостоятельной работы при выполнении различных заданий на уроке.

Тип урока: обобщающий урок с элементами математического моделирования

Форма: урок – игра

Методы обучения: иллюстративно-наглядные, развивающие, проблемно-поисковые.

Форма работы: индивидуальная, работа в парах, самостоятельная работа.

Оборудование: компьютер, проектор, карточки с заданиями.

Урок проводился в 6 «а» и 6 «б» классах, использовали два кабинета. Кабинет № 1- Игровая, кабинет № 2 – Математическая мастерская. Учащиеся классов работали в каждом кабинете по 20 минут.

План урока

1.Организационный момент (сообщение темы, цели и задачи урока).

2.Игровой момент (кроссворд, игра «поймай рыбку», игра «Лучший художник»)

3.Математическая мастерская с творческим заданием (изготовление листа Мёбиуса и применение его на практике)

4.Рефлексия. Подведение итогов.

Ход урока

1. Организационный момент.

2. Игровой момент (кроссворд) –дети работают в парах, их задача из предложенных слов составить кроссворд (8 минут)

1) Кроссворд

м

е

т

р

г

р

а

м

м

с

о

т

к

а

а

л

г

е

б

р

а

к

и

л

о

м

е

т

р

п

а

р

а

л

л

е

л

е

п

и

п

е

д

т

о

н

н

а

с

а

н

т

и

м

е

т

р

к

р

у

г

к

в

а

д

р

а

т

Вставить слова в кроссворд: параллелепипед, тонна, круг, сотка, алгебра, сантиметр, километр, квадрат, грамм, метр.

Математика – наука о величинах и количествах; всё что можно выразить цифрой, принадлежит математике(из толкового словаря В.И. Даля)

2) Кроссворд – угадай выделенное слово (кроссворд начерчен на доске, учитель задает вопросы), после разгаданного слова- Ковалевская, идет историческая справка.

к

у

б

х

о

р

д

а

у

р

а

в

н

е

н

и

е

р

а

д

и

у

с

л

и

н

е

й

к

а

п

р

о

ц

е

н

т

в

ы

ч

и

т

а

н

и

е

ч

и

с

л

и

т

е

л

ь

ц

и

р

к

у

л

ь

м

а

с

ш

т

а

б

т

ы

с

я

ч

а

1. Объёмное тело, каждая грань которого является квадратом.

2. Отрезок, соединяющий две любые точки окружности.

3. Равенство, где есть неизвестное число.

4. Отрезок, соединяющий центр окружности с любой её точкой.

5. Инструмент для измерения длины отрезка.

6. Сотая часть числа.

7. Действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое.

8. Число в записи дроби.

9. Инструмент для построения окружности.

10. Отношение длины отрезка на карте к длине соответствующего отрезка на местности.

11. Сто десятков – это сколько?

Слайд про С.В. Ковалевскую

3. Игра «Поймай рыбку» (игра на компьютере) – на слайде высвечивается координатная плоскость и в разных местах появляются рыбки. Учащиеся должны угадать координаты данных рыб.

4. Игра «Лучший художник»

Дети работают индивидуально по карточкам, рисуя животного в координатной плоскости по заданным точкам.

Утенок

1) (3; 0), (1; 2), (–1; 2), (3; 5), (1; 7), (–3; 6),

(–5; 7), (–3; 4), (–6; 3), (–3; 3), (–5; 2), (–5; –2),

(–2; –3), (–4; –4), (1; –4), (3; –3), (6; 1), (3; 0)

2) Глаз (–1; 5).

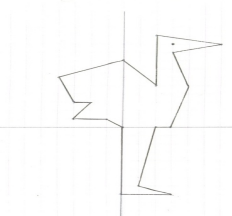
Страус

1. (0; 0), (- 1; 1), (- 3; 1), (- 2; 3), (- 3; 3), (- 4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4; 5), (3; 0), (2; 0),

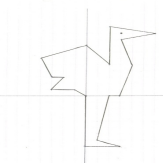
(1; - 7), (3; - 8), (0; - 8), (0; 0).

2) Глаз: (3; 10).

5. Игровой момент с творческим заданием ( лист Мёбиуса)

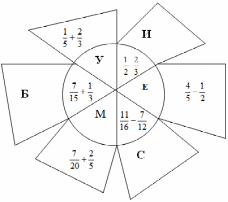
Ведущий: Найдите фамилию немецкого математика, решив примеры. Ответ и соответствующую букву запишите в таблицу и вы прочитаете фамилию ученого.

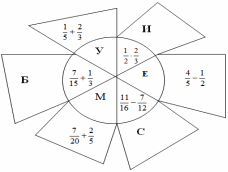
Ответы заносятся в таблицу.

Если команда правильно решила примеры и правильно заполнила таблицу, то получили фамилию немецкого ученого МЁБИУС.

Сообщение старшеклассницами о листе Мёбиуса в виде презентации и показ ими мастер класса «Лист Мёбиуса».

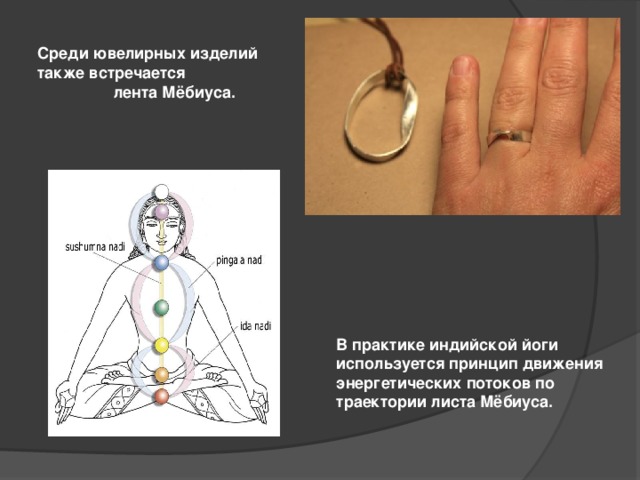
Лист Мёбиуса, лента Мёбиуса — топологический объект, простейшая односторонняя поверхность с краем. Попасть из одной точки этой поверхности в любую другую можно, не пересекая края. Лента Мёбиуса была обнаружена независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году. Модель ленты Мёбиуса может легко быть сделана. Для этого надо взять достаточно вытянутую бумажную полоску и соединить концы полоски, предварительно перевернув один из них. (делаем модель Мёбиуса с детьми)

• Лента Мёбиуса обладает любопытными свойствами. Если попробовать разрезать ленту вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двухсторонняя (вдвое больше закрученная, чем лента Мёбиуса) лента, которую фокусники называют «афганская лента». (делаем с детьми)

• Если теперь эту ленту разрезать вдоль посередине, получаются две ленты намотанные друг на друга. Если же разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более тонкая лента Мёбиуса, другая — длинная лента с двумя полуоборотами (Афганская лента). (делаем с детьми)

Девочки 8 класса Носкова Ирина и Волоскова Марина рассказывают с помощью презентации о свойствах и применении листа Мёбиуса.

6.Рефлексия. Подведение итогов.

Выводы:

вспомнили основные математические термины, решая кроссворд;

закрепили знания по теме координатная плоскость;

узнали много нового и интересного о математическом объекте лист Мёбиуса и его применении в жизни;

создали модель лист Мёбиуса.

7. Выставление оценок.

8. Домашнее задание: придумать задания с координатами, чтобы получилась фигура.

Используемая литература:

1. Учебник 6 класса, автор учебника Н.Я. Виленкин;

2. Математика «Занятие школьного кружка», авторы О.С. Шейкина, Г.М. Сольвьева.

3.Математика. Учебник-собеседник, Л.Н Шеврин, И.О. Гейн, М.В. Попов.

4.Интернет ресурсы

Рецензия на урок математики

в 6-х классах

по теме: «Координатная плоскость»

Данный урок – урок игра, с элементами математического моделирования. Урок повторения, систематизации и обобщения знаний, закрепления умений и навыков по темам: «Координатная плоскость», «Геометрические фигуры» , что определяет его цели и задачи.

На уроке прослеживаются элементы игровой, здоровьесберегающей технологии и технологии проблемного обучения и ИКТ.

Реализация поставленной цели и задач происходит на уроке в процессе постоянно сменяющихся учебных ситуаций, что отражено в структуре урока и в использовании учителями таких методических приёмов, как сообщения учащихся (презентация), беседа по вопросам, разгадывание кроссворда, создание собственной модели и построение различных фигур на координатной плоскости.

Задания у обучающихся формируют интерес к предмету, развивают внимание, навыки самостоятельной работы при выполнении различных заданий на уроке.

Сообщения учащихся позволяют в полной мере реализовать как образовательный, так и воспитательный потенциал урока.

При выборе методов и форм обучения учащихся для достижения поставленной цели учителями (Иванова Галина Николаевна, Мурашкина Виктория Владимировна ) были учтены основные принципы:

• принцип внимания к подбору материала: исторический материал, кроссворд, презентация;

• принцип доступности материала: предлагаемый на уроке материал соответствует возрасту учащихся и их жизненному опыту.

Организации интересного урока способствовало и эффективное применение технических средств – мультимедийного оборудования (игра «Поймай рыбку»).

Урок получился интересным, эффективным и плодотворным, не оставил равнодушными никого (все с энтузиазмом приняли предложенное творческое домашнее задание).

Цель урока достигнута, задачи реализованы.

Заместитель директора по УВР

Никитина Н.П.

Приложения

Приложение 11

1) Кроссворд

м

е

т

р

г

р

а

м

м

с

о

т

к

а

а

л

г

е

б

р

а

к

и

л

о

м

е

т

р

п

а

р

а

л

л

е

л

е

п

и

п

е

д

т

о

н

н

а

с

а

н

т

и

м

е

т

р

к

р

у

г

к

в

а

д

р

а

т

2) Кроссворд

к

у

б

х

о

р

д

а

у

р

а

в

н

е

н

и

е

р

а

д

и

у

с

л

и

н

е

й

к

а

п

р

о

ц

е

н

т

в

ы

ч

и

т

а

н

и

е

ч

и

с

л

и

т

е

л

ь

ц

и

р

к

у

л

ь

м

а

с

ш

т

а

б

т

ы

с

я

ч

а

Приложение 2 2

Утенок

1) (3; 0), (1; 2), (–1; 2), (3; 5), (1; 7), (–3; 6),

(–5; 7), (–3; 4), (–6; 3), (–3; 3), (–5; 2), (–5; –2),

(–2; –3), (–4; –4), (1; –4), (3; –3), (6; 1), (3; 0)

2) Глаз (–1; 5).

Страус

1. (0; 0), (- 1; 1), (- 3; 1), (- 2; 3), (- 3; 3), (- 4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4; 5), (3; 0), (2; 0),

(1; - 7), (3; - 8), (0; - 8), (0; 0).

2) Глаз: (3; 10).

Приложение 3 3

Приложение 44

Известный математик Софья Васильевна Ковалевская была дочерью генерал-лейтенанта артиллерии В.В. Корвин-Круковскаго и Елены Федоровны Шуберт. Дядя ее с материнской стороны был известным математиком, а прадед еще более выдающимся астрономом.

Приложение 5 5

На уроке

Лист Мёбиуса , лента Мёбиуса  — топологический объект, простейшая односторонняя поверхность с краем.

Попасть из одной точки этой поверхности в любую другую можно, не пересекая края.

Модель ленты Мёбиуса может легко быть сделана. Для этого надо взять достаточно вытянутую бумажную полоску и соединить концы полоски, предварительно перевернув один из них.

• Лента Мёбиуса обладает любопытными свойствами. Если попробовать разрезать ленту вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двухсторонняя лента, которую фокусники называют «афганская лента».

• Лента Мёбиуса была обнаружена независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году.

Ранее считалось, что любая поверхность (например, лист бумаги) имеет две стороны. Мёбиус сделал поразительное открытие – получил поверхность, которая имеет лишь одну сторону.

• Мёбиус Август Фердинанд Листинг Иоганн Бенедикт

Искусство и технология

Международный символ переработки

представляет собой Лист Мёбиуса.

Чудесные свойства ленты тут же

породили множество научных трудов, изобретений, а также многочисленных фантастических рассказов.

Чудесные свойства ленты Мебиуса породили множество фантастических рассказов.

• В одном из них описывался случай в Нью-Йоркском метро , когда потерялся во времени поезд , отправившейся в путь по сути , замкнутом в ленту Мебиуса.
• А в рассказе известного писателя-фантаста Артура Кларка « Стена Мрака» один из героев совершает путешествие по необычной планете , изогнутой в виде листа Мебиуса.

• Лента Мебиуса наблюдается в форме ремней для заточки инструмента , красящей лентой для печатающих устройств , ременной передачей так как её поверхность будет изнашиваться вдвое медленнее . A магнитофонная лента , расположенная в кассете по ленте Мебиуса, будет проигрываться в два раза дольше.

Невероятный проект

новой библиотеки в

Астане, Казахстан.

Лента Мёбиуса в скульптуре представлена в различных вариантах:

от традиционных до самых невероятных…

Данная скульптура

составлена из множества

консервных банок

Лист Мёбиуса и

шар

Монумент у здания Президиума Национальной академии наук

В Минске

Памятник ленте Мёбиуса

в Москве

Среди ювелирных изделий

также встречается

лента Мёбиуса.

В практике индийской йоги

используется принцип движения

энергетических потоков по

траектории листа Мёбиуса.

Лист Мёбиуса служил вдохновением для скульптур и для графического искусства.

•   Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — лист Мёбиуса II, показывает муравьёв, ползающих по поверхности ленты Мёбиуса.

Лист Мебиуса – символ математики, Что служит высшей мудрости венцом… Он полон неосознанной романтики: В нем бесконечность свернута кольцом. В нем – простота, и вместе с нею – сложность, Что недоступна даже мудрецам:

Здесь на глазах преобразилась плоскость В поверхность без начала и конца. Здесь нет пределов, нет ограничений, Стремись вперед и открывай миры, Почувствуй силу новых ощущений, Прими познанья высшего дары.