Тема:. Решение задач. Подготовка к Контрольной работе
Цели и задачи урока: Создать условия для повторения, закрепления материала главы I; совершенствовать навыки решения задач; подготовить учащихся к предстоящей контрольной работе
Предметные умения: Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности
УУД
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям.
Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок: осуществляют самоанализ и самоконтроль.
Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.
Личностные: осознают важность и необходимость изучения предмета
Проверка домашнего задания. К доске вызываются двое учащихся.
№ 66.
(Ф/И)
Проверка домашнего задания. К доске вызываются двое учащихся.
№ 66.
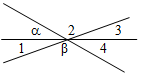
а) Если Ð2 + Ð4 = 220°, так как Ð2, Ð4 – вертикальные, то Ð2 = Ð4 = 220° : 2 = 110°.
Ð1 = Ð3 = 70° (смежные с Ð2 и Ð4).
Рис. 1
Ответ: 70°, 110°, 70°, 110°.
б) Если 3 · (Ð1 + Ð3) = Ð2 + Ð4, в) Если Ð2 – Ð1 = 30°. Примем Ð1 = х, следовательно:
так как Ð1 = Ð3 = х, Ð2 = х + 30°
то Ð2 = Ð4 = 180° – х подставим в условие: х + х + 30° = 180°
3 · (х + х) = 180° – х + 180° – х 2х = 150°
6х = 360° – 2х х = 75°
8х = 360° Ð1 = 75°, Ð2 = 105°
х = 45° Ответ: 75°, 105°.
Ð1 = Ð3 = 45°, Ð2 = Ð4 = 135°
Ответ: 45°, 135°, 45°, 135°.
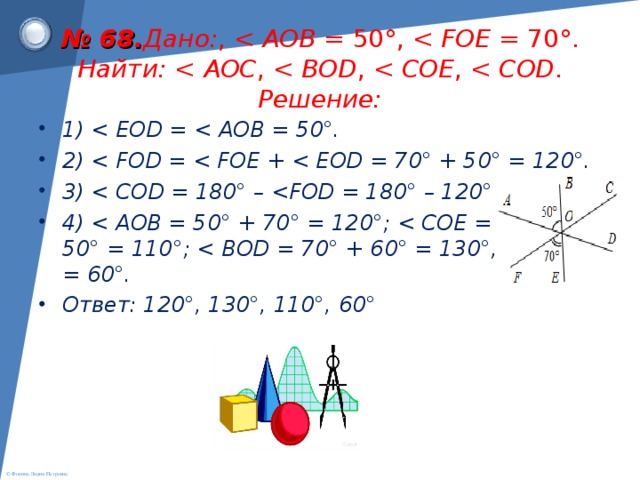
№ 68.
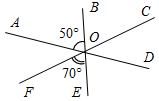
Дано: AD Ç BE Ç FC = O, ÐAOB = 50°, ÐFOE = 70°.
Найти: ÐАОС, ÐBOD, ÐCOE, ÐCOD.
Рис. 2
Решение:
1) ÐEOD = ÐAOB = 50°.
2) ÐFOD = ÐFOE + ÐEOD = 70° + 50° = 120°.
3) ÐCOD = 180° – ÐFOD = 180° – 120° = 60°.
4) ÐAOB = 50° + 70° = 120°; ÐCOE = 60° + 50° = 110°; ÐBOD = 70° + 60° = 130°, ÐCOD = 60°.
Ответ: 120°, 130°, 110°, 60°
II этап. Самостоятельная работа
Задания для самостоятельной работы
(И) Работа рассчитана на 10–15 минут. Далее осуществляется взаимопроверка.
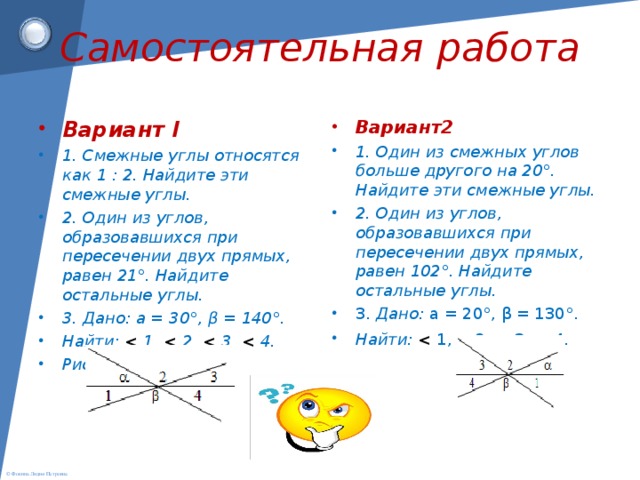
Вариант I
1. Смежные углы относятся как 1 : 2. Найдите эти смежные углы.
2. Один из углов, образовавшихся при пересечении двух прямых, равен 21°. Найдите остальные углы.
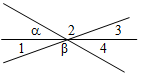
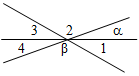
3. Дано: a = 30°, β = 140°.
Найти: Ð1, Ð2, Ð3, Ð4.
Рис. 3
Вариант II
1. Один из смежных углов больше другого на 20°. Найдите эти смежные углы.
2. Один из углов, образовавшихся при пересечении двух прямых, равен 102°. Найдите остальные углы.
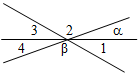
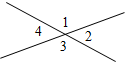
3. Дано: a = 20°, β = 130°.
Найти: Ð1, Ð2, Ð3, Ð4.
Рис. 4
Решение:
Вариант I
1. Так как Ð1 : Ð2 = 1 : 2, то Ð1 = х, Ð2 = 2х. Но Ð1 + Ð2 = 180°, тогда х + 2х = 180°, х = 60, значит, Ð1 = 60°, Ð2 = 120°.
Рис. 5
2. Пусть Ð1 = 21°, тогда Ð3 = Ð1, как вертикальные, и Ð3 = 21°. Ð1 и Ð2 – смежные и Ð1 + Ð2 = 180°.
Тогда Ð2 = 180° – Ðl = 159°. Но Ð2 = Ð4, как вертикальные, значит, Ð4 = 159°.
Рис. 6
3. a = 30°, тогда Ð4 = 30°, так как Ð4 и угол с градусной мерой a – вертикальные. β = 140°, тогда Ð2 = 140°, так как Ð2 и угол с градусной мерой β – вертикальные.
Ð2 + Ð3 + Ð4 = 180°, тогда Ð3 = 180° – (Ð2 + Ð4) = 10°.
Ð3 и Ð1 – вертикальные, поэтому Ð3 = Ð1, Ð1 = 10°.
Вариант II
1. Ð2 на 20° больше Ð1, тогда Ð1 = х, Ð2 = х + 20°. Но Ð1 + Ð2 = 180°, тогда х + х + 20° = 180°, х = 80°, значит, Ð1 = 80°, Ð2 = 100°.
Рис. 7
2. Пусть Ð1 = 102°, тогда Ð3 = Ð1, как вертикальные, и Ð3 = 102°. Ð1 и Ð2 – смежные и Ð1 + Ð2 = 180°, тогда Ð2 = 180° – Ð1 = 78°. Но Ð2 = Ð4, как вертикальные, значит, Ð4 = 78°.
Рис. 8
3. a = 20°, тогда Ð4 = 20°, так как Ð4 и угол с градусной мерой a – вертикальные. β = 130°, тогда Ð2 = 130°, так как Ð2 и угол с градусной мерой β – вертикальные.
Ð2 + Ð3 + Ð4 = 180°, тогда Ð3 = 180° – (Ð2 + Ð4) = 30°.
Ð3 и Ð1 – вертикальные, поэтому Ð3 = Ð1, Ð1 = 30°
III этап. Тест
Тестовые задания
(И)
1. Точка С лежит на луче АВ. Какая из точек А, В, С лежит между двумя другими?
а) А; в) С;
б) В или С; г) В.
2. Отрезок ХМ пересекает прямую а. Отрезок XD пересекает прямую а. Пересекает ли прямую а отрезок МD?
а) Да; в) никогда не пересекает;
б) может не пересекать; г) нет правильного ответа.
3. Один из углов, образованных при пересечении двух прямых, – прямой. Остальные углы…
а) острые и прямой; в) прямые;
б) тупые и прямой; г) нет правильного ответа.
4. Сумма двух углов, образованных при пересечении двух прямых, равна 180°. Эти углы…
а) смежные; в) нет правильного ответа;
б) вертикальные; г) могут быть смежными, могут быть вертикальными.
5. Если точка В принадлежит отрезку АС, то.
а) АВ + ВС = АС; в) ВС + АС = АВ;
б) АВ + АС = ВС; г) нет правильного ответа.
6. Если луч ОС проходит между сторонами угла АОВ, то.
a) ÐAOC = ÐBOC; в) ÐAOB + ÐBOC = ÐAOC;
б) ÐAOC + ÐBOC = ÐAOB; г) ÐAOC + ÐAOB = ÐBOC.
7. Если точка В – середина отрезка АС, то…
а) АВ + ВС = АС; в) АВ = 2АС;
б) АС = ВС; г) АС = 2АВ.
8. Если луч ОС – биссектриса ÐAOB, то…
a) ÐAOB = ÐAOC + ÐBOC; в) ÐAOC = ÐBOC;
б) ÐAOC = ÐAOB; г) ÐAOB ≠ ÐBOC.
Ответы: 1 – б; 2 – г; 3 – в; 4 – г; 5 – а; 6 – б; 7 – г; 8 – в