Муниципальное казённое общеобразовательное учреждение
«Средняя общеобразовательная школа №6»
г. Киров Калужской области
Урок геометрии в 7 классе
«Сумма углов треугольника»
Выполнила:Балалаева М.Н.
Учитель математики
Высшая квалификационная категория
2014 год
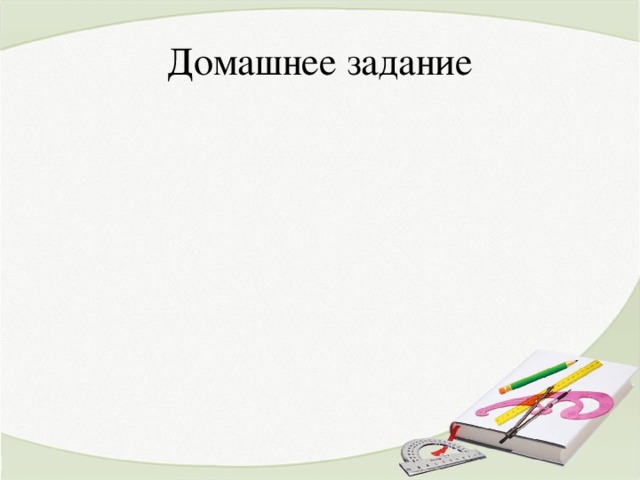
Тема урока: Сумма углов треугольника
Цели урока: Найти сумму углов треугольника, сформулировать и доказать теорему о сумме углов треугольника, ввести понятие остроугольного, прямоугольного и тупоугольного треугольника; научить решать задачи на применение нового материала.
Задачи урока:
-образовательные (формирование познавательных УУД):
научить поиску и выделение необходимой информации, самостоятельное выделять и формулировать познавательную цель, выбирать наиболее эффективный способ решения задачи, построению логической цепи рассуждений и доказательству.
- воспитательные (формирование коммуникативных и личностных УУД):
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
- развивающие (формирование регулятивных УУД):
умение планировать и прогнозировать свою деятельность, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Тип урока – урок открытия новых знаний.
Формы работы учащихся: фронтальная, парная, индивидуальная, групповая.
Необходимое техническое оборудование: доска школьная, компьютер, проектор, интерактивная доска, раздаточный материал (рабочий лист к уроку, карточки с заданием в группе и тестом, треугольник, вырезанный из цветной бумаги), электронная презентация, выполненная в программе Power Point.
Ход урока:
Оргмомент
Встали тихо, замолчали,
Всё, что нужно, вы достали.
Приготовились к уроку,
В нём иначе нету проку.
Здравствуйте, садитесь,
Все мне дружно улыбнитесь.
У нас с вами сегодня не совсем обычный урок. На нем присутствуют гости-учителя нашей школы. А поэтому
Будем отвечать активно,
Хорошо себя вести,
Чтобы гости дорогие.
Захотели вновь придти!
- Сегодня на уроке мы приступаем к изучению последней главы нашего учебника.
- Но прежде чем начать ее изучение, давайте вернемся к началу и вспомним что изучает наука геометрия?
- Ответьте на следующий вопрос.: изучению какой геометрической фигуры мы уделяли больше всего внимания в 7 классе?
- Правильно. Это треугольник
- А как вы считаете, почему именно с треугольника мы начали изучение геометрии в 7 классе?(Треугольник – самая простая фигура)
- В старших классах каждый школьник
Изучает треугольник.
Три каких-то уголка,
А работы - на века.»
- Давайте вспомним, что важного о треугольнике мы уже узнали в 7 классе?
Постановка учебной проблемы:
Мотивация изучения теоремы:
- Действительно, мы умеем строить треугольники, умеем их сравнивать, знаем названия его элементов. Решите задачу(на готовых чертежах)
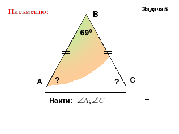
Задача: Дан 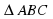 . Р=24см.
. Р=24см.
1)Найдите неизвестные стороны 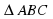 , если
, если
а) АВ= ВС=5см б) АВ=ВС, АС=14см в) АВ=ВС=АС
2)Найдите неизвестные углы 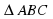 , если :
, если :
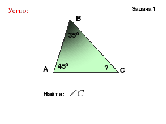
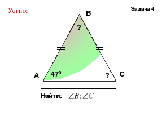
а) АВ=ВС, ∠А=20° б)АВ=ВС, ∠В=120° в)АВ=ВС=АС
-Можете ли мы найти все углы треугольника??
- Итак, мы не можем решить задачу, так как не знаем, как связаны между собой углы треугольника.
- Подведем первый итог нашей работы. Мы установили, что, имеющиеся знания не позволяют нам решать определенного рода задачи нам не известно очень важное свойство треугольника, играющее существенную роль в геометрии и в применении геометрии на практике. Поэтому, цель сегодняшнего урока - получить ответ на вопрос: каким соотношением связаны углы треугольника?
Составим план наших действий:
Нужно найти соотношение, связывающее три угла треугольника
Нужно его обосновать (убедиться, что оно выполняется для любого
треугольника).
Нужно учиться применить его в решении задач
Эпиграфом нашего урока будут слова российского и советского математика, доктора физико-математических наук, профессора МГУ Вениамина Фёдоровича Кагана «Легче остановить Солнце, Легче двинуть Землю, чем изменить сумму углов треугольника»
Работа над новой темой
Раскрытие содержания теоремы
Давайте же выясним, каким свойством обладают углы любого треугольника
- Сейчас мы с вами превратимся в группу исследователей. Проведем практические работы. Их цель - получить информацию об углах в различных треугольниках.
Практическое задание №1: Начертите в тетради любой треугольник. Измерьте его углы и запишите результаты измерений. Найдите сумму углов треугольника. Транспортир будет инструментом нашего исследования
Сравним полученные результаты. На доску выносится таблица и результаты измерения нескольких учащихся.
Почему некоторые суммы совпали, а некоторые – нет? От чего это зависит?
- Похоже, что все крутится вокруг 180°, т.е. сумма всех трех углов есть величина, близкая к 180°, в каждом из рассмотрении» примеров.
- Как вы думаете, мы уже можем выдвинуть гипотезу
- А почему не везде получается одинаковое число?
- Я тоже считаю, что выдвинутая гипотеза правомерна, мы ведь знаем с вами что, ни одно измерение не дает абсолютно точных результатов. Но, несомненно, выдвинутая гипотеза нуждается в проверке
- Первоначальную проверку мы можем осуществить опытным путем.
Практическое задание №2:
В желтом треугольнике обозначьте углы через №1, №2, №3. Оторвите их и совместите вершины углов так, чтобы образовался развернутый угол.
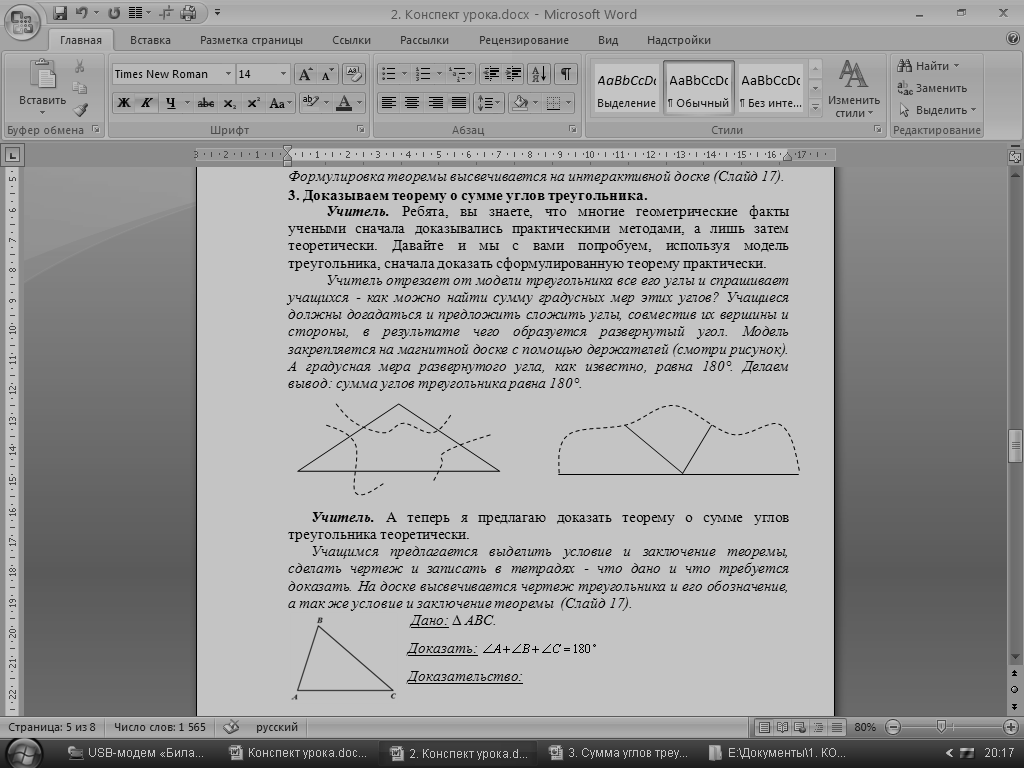
Практическое задание №3
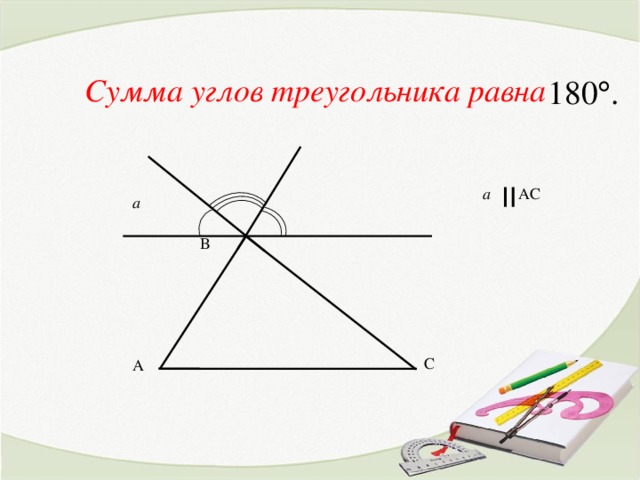
Расположите три равных треугольника так, чтобы получились параллельные прямые и углы №1, №2, №3 составили развернутый угол.

Вопросы учителя:
Что общего между выполненными заданиями вы заметили?
Какой промежуточный вывод можно сделать?
Случайно ли сумма углов треугольников оказалась равной 180° или этим свойством обладает любой треугольник? (создание проблемной ситуации)
Вы получили результат практически. Можно ли данное утверждение назвать гипотезой?
Что надо сделать с гипотезой, чтобы убедиться, что она справедлива для любого треугольника? (доказать)
Как называется утверждение, справедливость которого надо доказать? (теорема)
Мотивация необходимости доказательства теоремы
Как вы уже знаете, нельзя выполнить ни абсолютно точных построений, ни произвести абсолютно точных измерений. Поэтому правильнее было бы сказать, что рассмотренные нами треугольники имеют сумму углов приблизительно равную 180°.Но такое утверждение относится только к рассмотренным нами треугольникам. Мы ничего не можем сказать о других треугольниках, так как их углы мы не измеряли.
Чтобы убедиться в том, что сумма углов треугольника точно равна 180° и притом для любого треугольника, нам ещё нужно провести соответствующие рассуждения, т.е доказать справедливость утверждения, подсказанного опытом.
Работа над структурой теоремы
- Какие треугольники использовались в процессе проведения измерений?
- Попробуйте сформулировать теоремы
- Переформулируйте теорему со словами «Если,….то…»
- Что входит в условие теоремы? Т.е, что дано в теореме?
-В чём состоит заключение теоремы? Т.е, что будем доказывать?
Построение чертежа и краткая запись теоремы
Дано: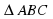 , ∠А=1, ∠В=2, ∠С=3
, ∠А=1, ∠В=2, ∠С=3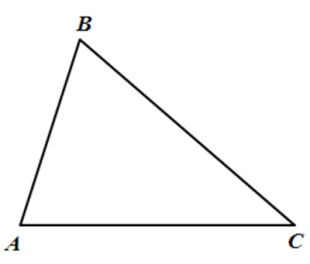
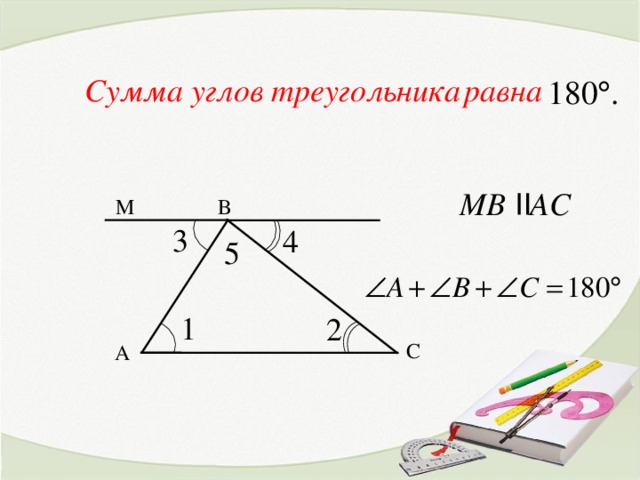
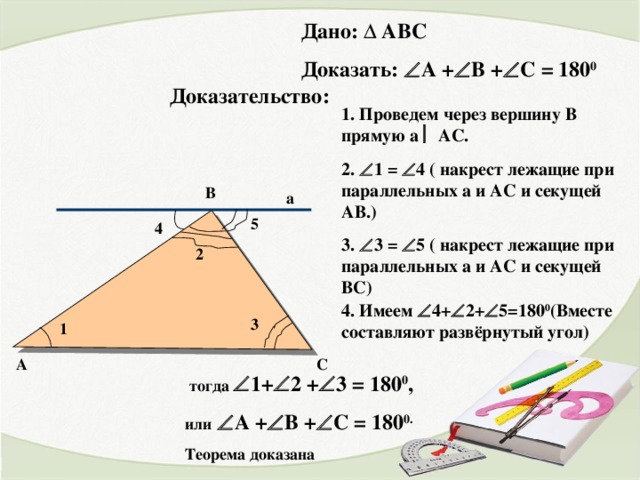
Доказать: ∠А+∠В +∠С=180°
Поиск доказательства теоремы:
Какие утверждения, связанные с величиной 180°, вам известны?
Развернутый угол равен 180°.
Сумма смежных углов равна 180°.
Сумма односторонних углов при параллельных прямых равна 180°.
Сумма углов треугольника равна 180°.
- Чтобы найти сумму углов треугольника, их надо сложить. Поэтому пойдём естественным путём: будем углы складывать. Попробуем собрать(Сложить все углы треугольника в одной вершине.
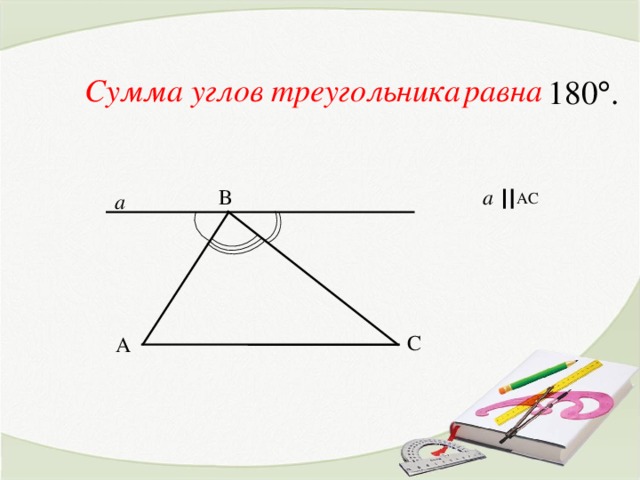
- Как это можно сделать?( провести через вершину угла В прямую, параллельную стороне АС)
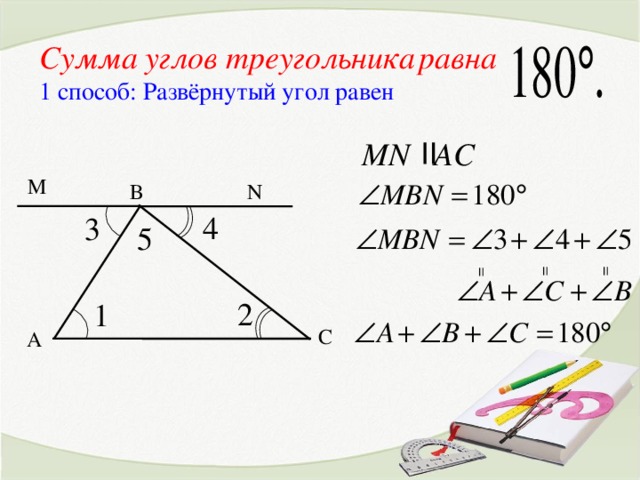
1способ доказательства: Развёрнутый угол =180°
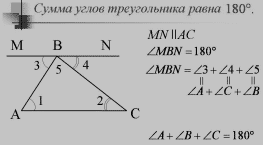
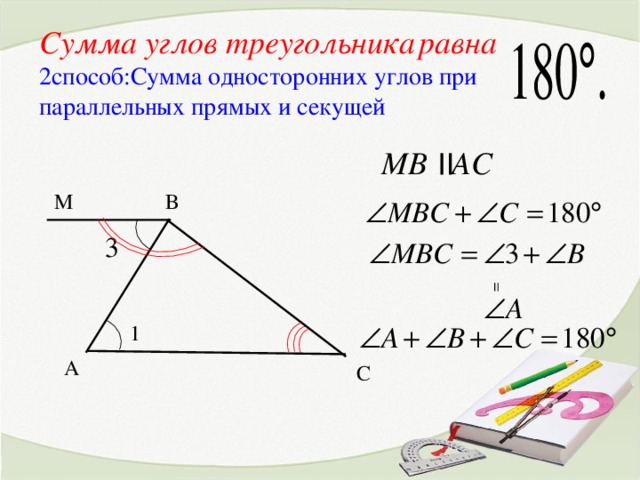
2 способ доказательства: Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180°
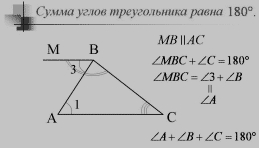
3 способ доказательства: Сумма смежных углов равна 180°
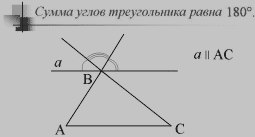
Физкультминутка
Первичное осмысление и закрепление знаний
Применение теоремы к решению задач на нахождение неизвестных углов треугольника
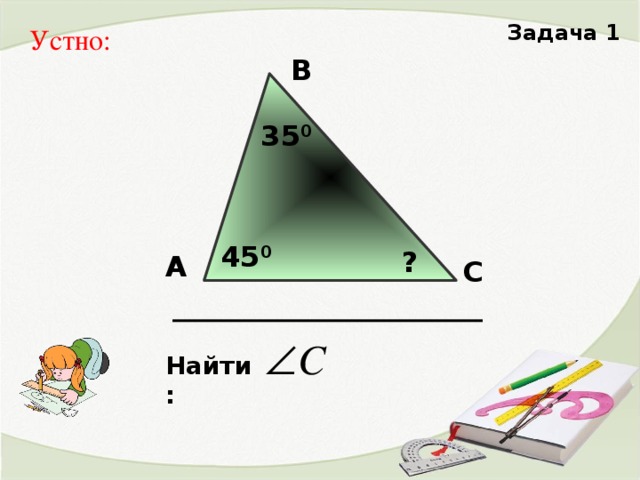
Устное решение задач:
1.Вернуться к задачам, вызвавшим затруднение в начале урока и решить их.
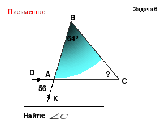
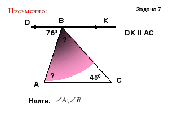
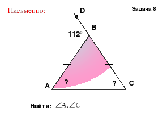
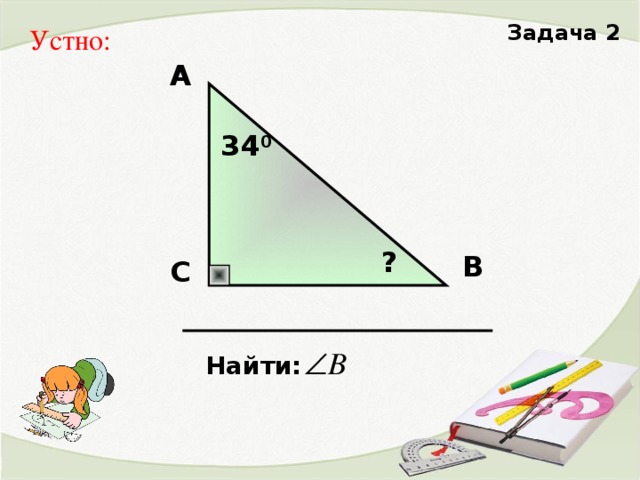
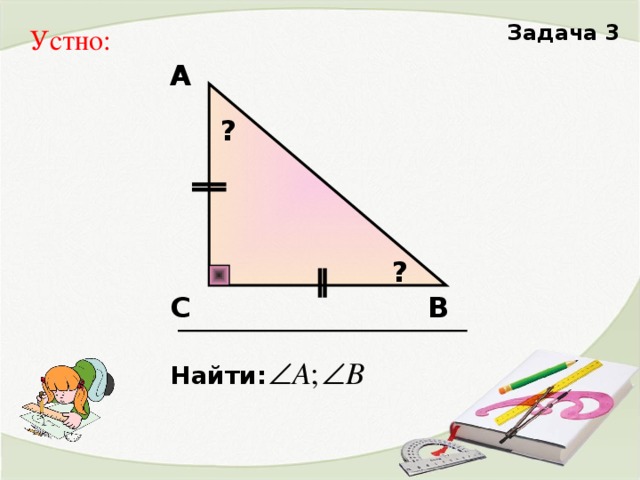
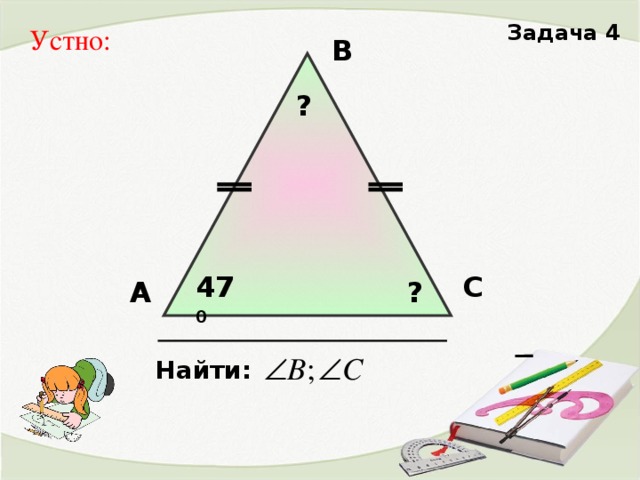
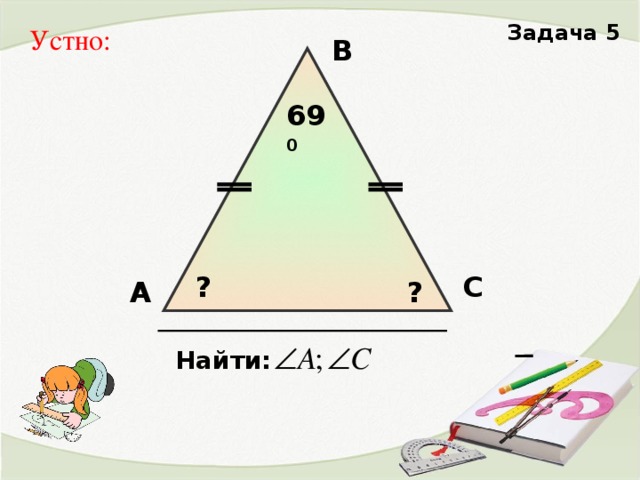
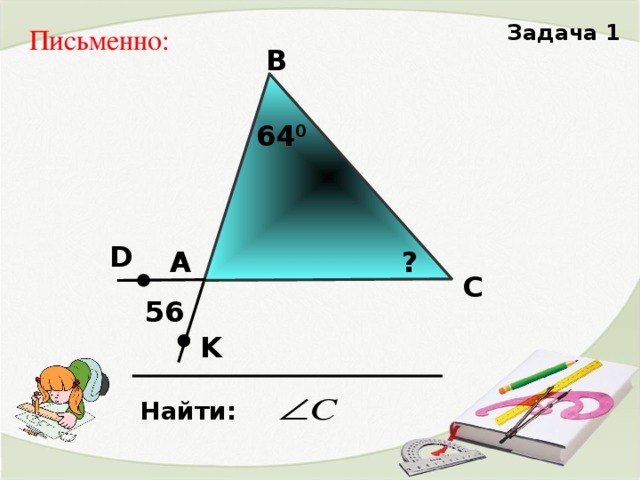
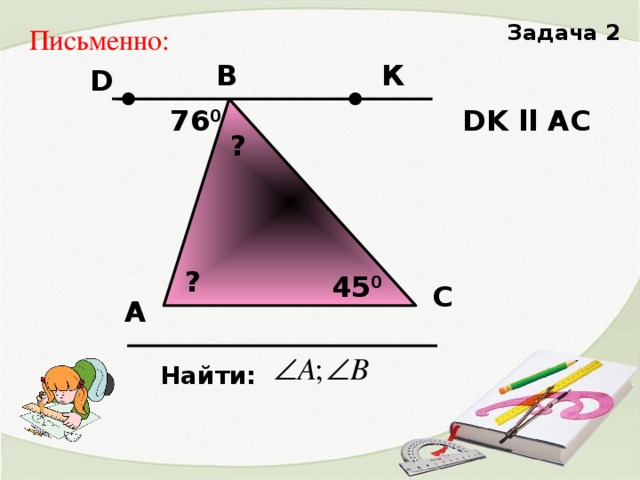
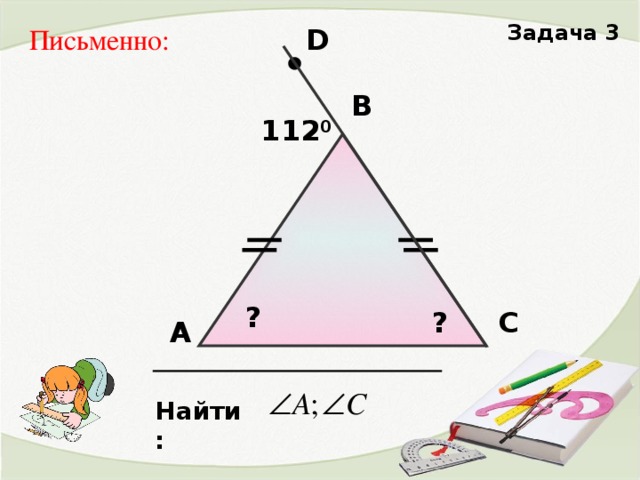
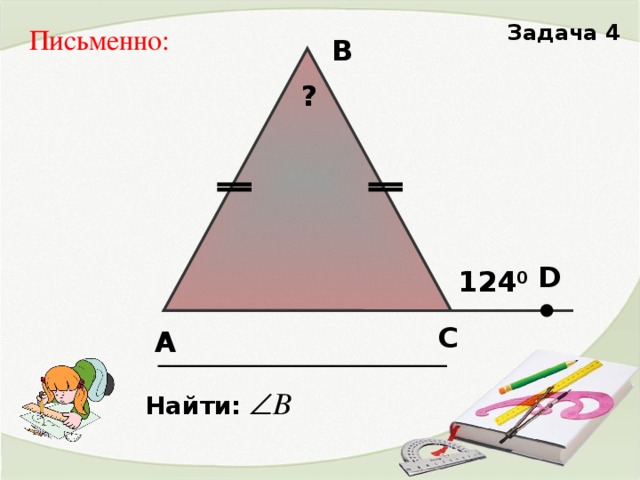
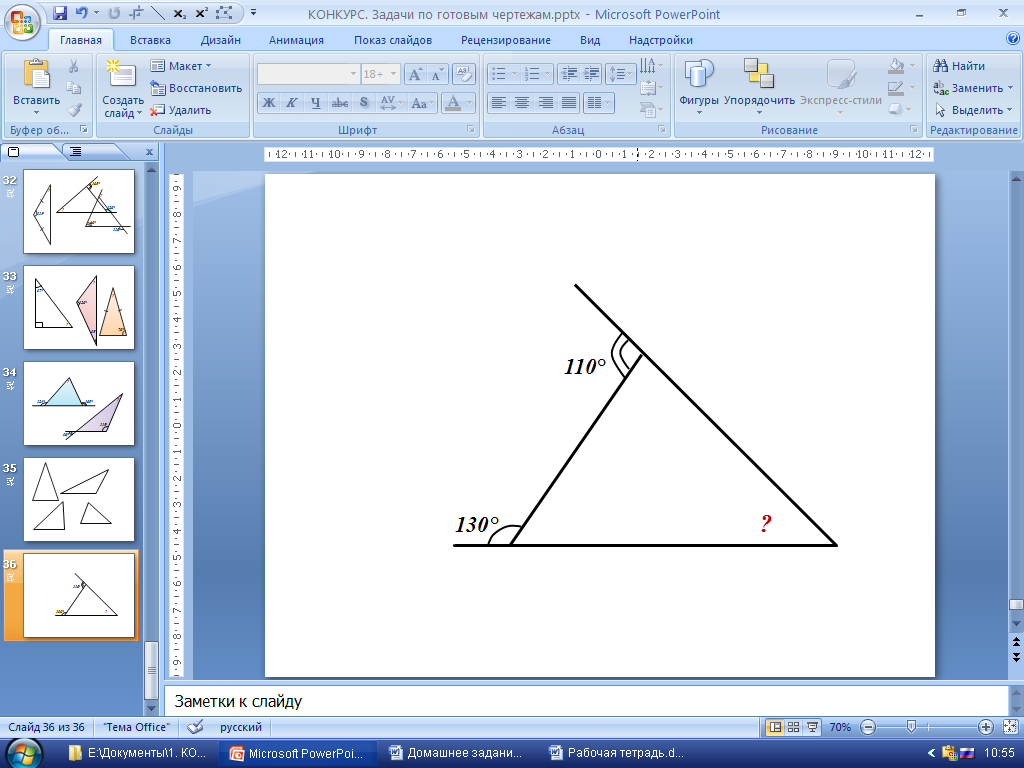
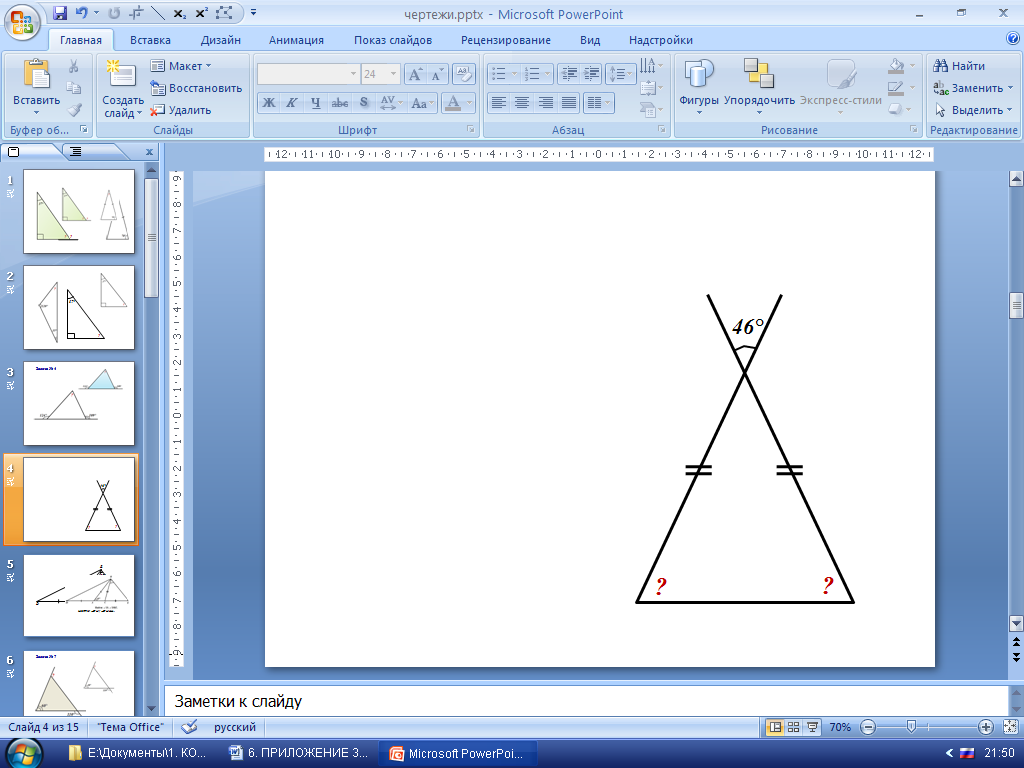
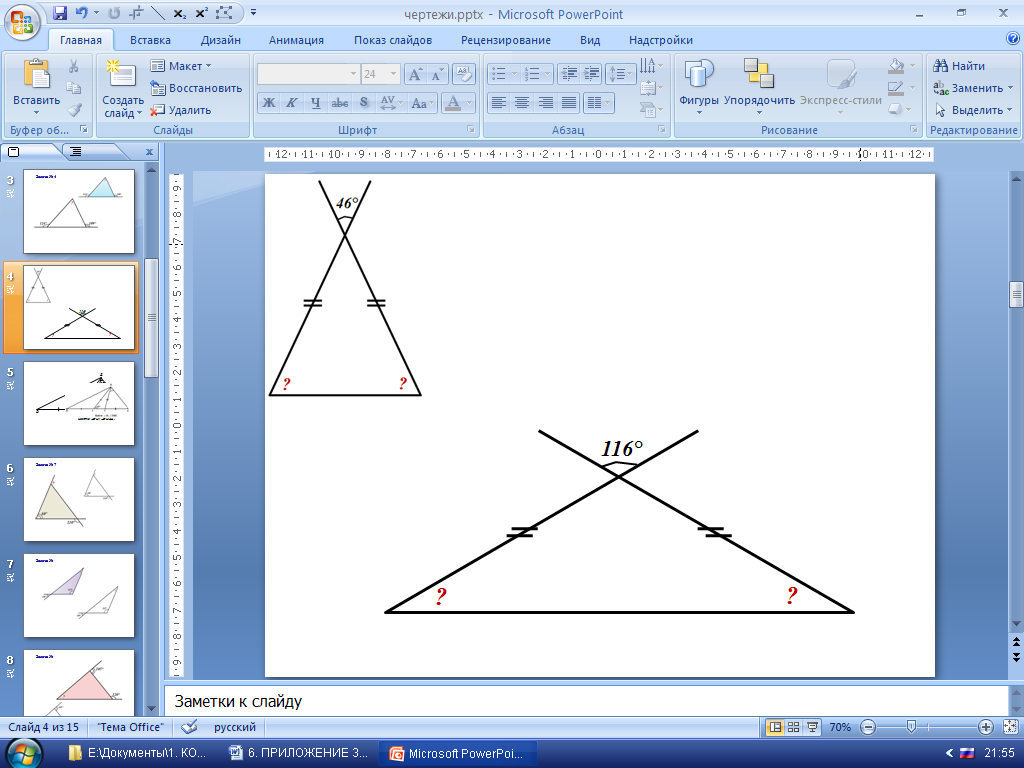
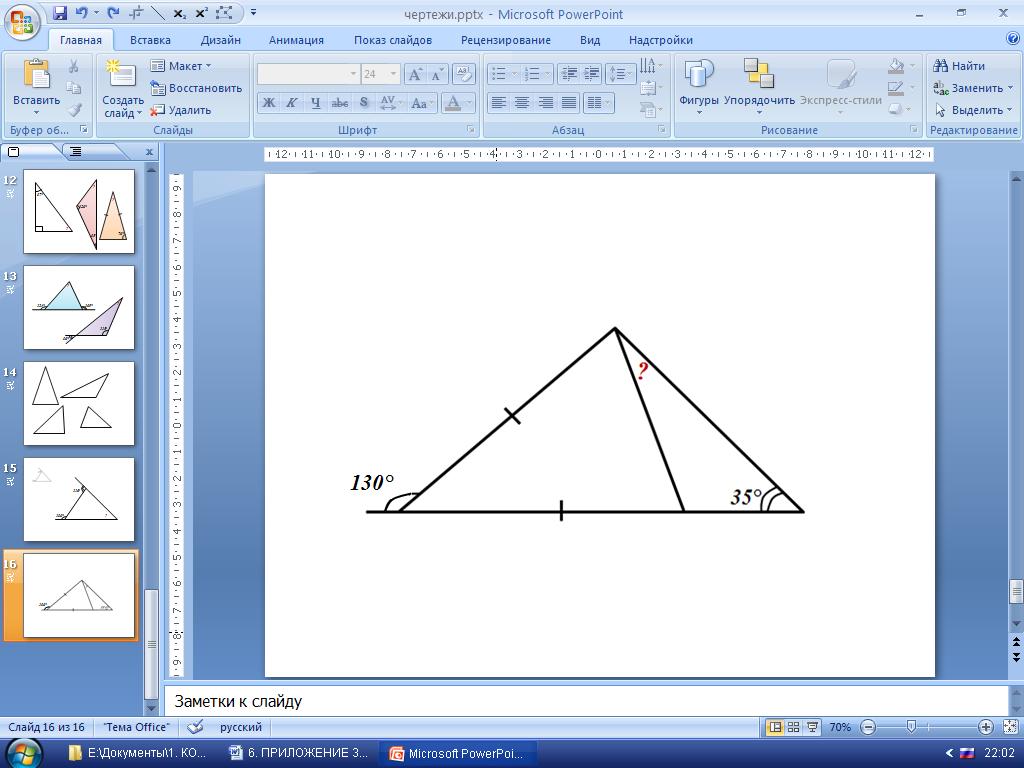
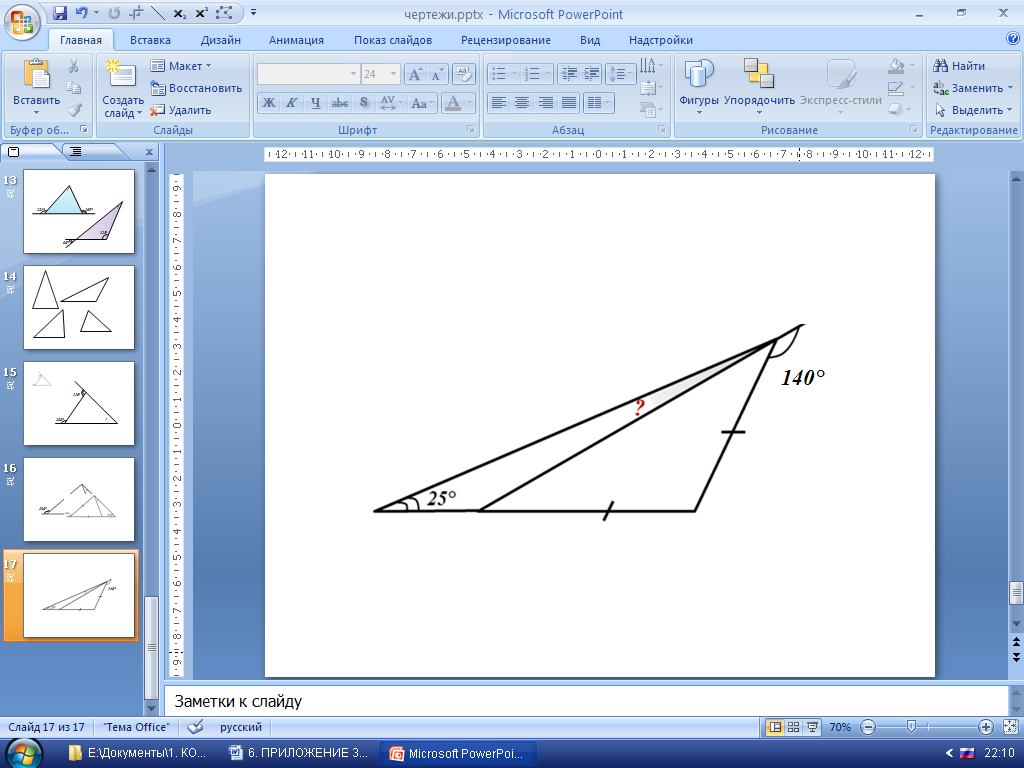
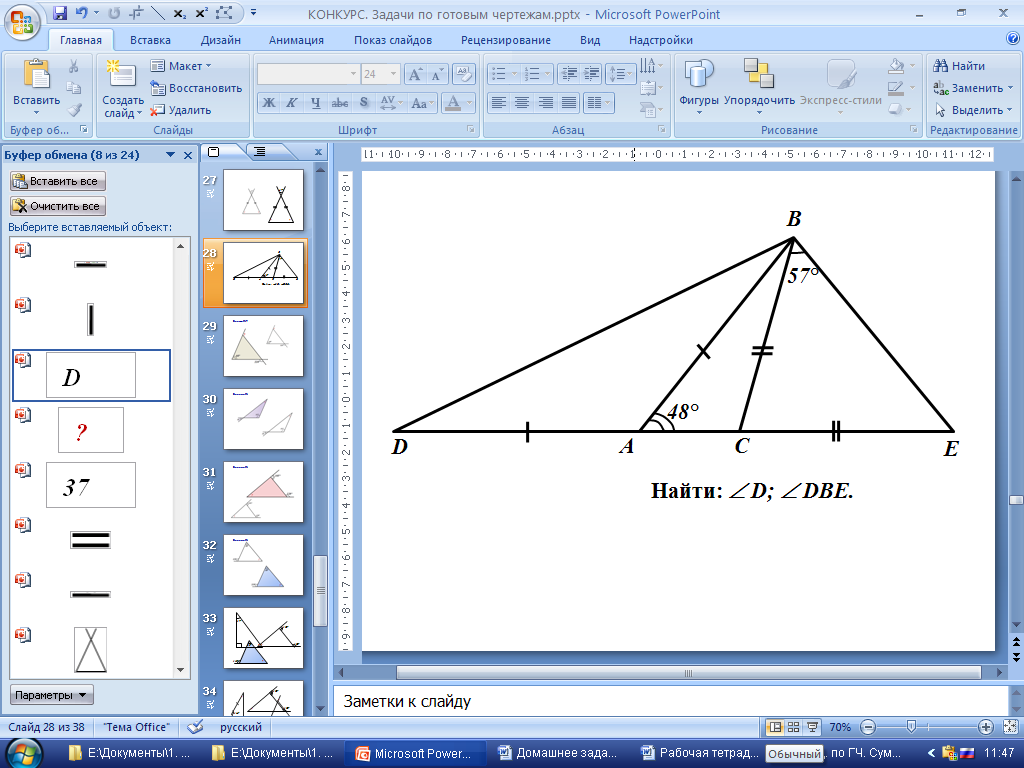
2. Решение задач на готовых чертежах
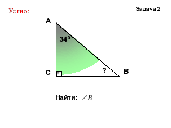
- Если один из углов треугольника прямой, что можно сказать о двух других углах?
- Если в треугольнике один угол прямой, чему равна сумма двух других углов?
- Если один из углов треугольника тупой, каковы другие 2 угла других углов?
- Могут ли все углы в треугольнике быть равными?
- Чему равна градусная мера каждого из них? Чему равна градусная мера каждого них?
- Могут ли все углы треугольника быть острыми?
- Бывают ли треугольники с двумя прямыми углами? С двумя тупыми углами?
С прямым и тупым углом?
Самостоятельная работа: Тест
| Вариант 1 Из предложенных утверждений выберите верное: 1.Два угла треугольника равны 44° и 96°.Чему равен третий угол? 1) 90° 2) 40° 3) 30° 2.Угол при вершине равнобедренного треугольника равен 120°. Найдите угол при основании треугольника. 1) 60° 2) 180° 3)30° 3. Один из острых углов прямоугольного треугольника равен 47°.Найдите второй острый угол. 1) 43° 2) 47° 3) 90° 4.Существует ли треугольник два угла которого равны 136° и 44°? 1) да 2) нет 3) не знаю 5.Существование какого треугольника невозможно: 1) у которого все углы острые; 2) у которого один угол тупой, а два острые; 3) у которого один угол прямой, а два острые; 4) у которого все углы по 60° 5) у которого два угла тупые
| Вариант 2 Из предложенных утверждений выберите верное: 1.Два угла треугольника равны 53° и 77°.Чему равен третий угол? 1) 60° 2) 50° 3) 90° 2.Угол при основании равнобедренного треугольника равен 20°. Найдите угол при вершине треугольника. 1) 60° 2) 140° 3)180° 3. Один из острых углов прямоугольного треугольника равен 33°.Найдите второй острый угол. 1) 33° 2) 57° 3) °90 4.Существует ли треугольник с углами, градусные меры которых равны 26°, 44° и 110°? 1) да 2) нет 3) не знаю 5. Какой из перечисленных треугольников существует: 1) у которого все углы тупые; 2) у которого все углы острые; 3) у которого два угла тупые, а один – острый; 4) у которого два угла прямые 5) у которого один угол – прямой, один – тупой; один – острый. |
Рефлексия
У Плутарха есть известная притча о работниках, которые под горячим солнцем везли тачки с камнями для строительства.. Работников было трое. К ним подошёл человек и задал каждому из них один и тот же вопрос: «Чем ты занимаешься?» Ответ первого был таков: «Везу эту проклятую тачку с тяжёлыми камнями». По-иному ответил второй: «просто выполняю свою работу, тем самым зарабатываю себе на хлеб». Третий воодушевлённо провозгласил: «Строю прекрасный храм».
Все они выполняли одну и ту же работу, но думали о ней, а, следовательно, и выполняли её по-разному.
Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.
- Кто возил камни? (поднимите синие треугольники)
- Кто выполнял свою работу? (поднимите желтые треугольники)
- Кто строил храм? (поднимите красные треугольники)
Из истории треугольников
В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о которой мы сегодня будем говорить. Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется «бермудским треугольником». А ещё его называют «дьявольский треугольник», «треугольник проклятых». Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа «бермудского треугольника» остаётся тайной и по сей день.
Учитель: , Свойства треугольника человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни (строительстве и земледелии), любой многоугольник можно диагоналями разделить на треугольники.
Действительно, хотя треугольник и самый простой по виду из многоугольников, но по количеству свойств он опережает многие более сложные фигуры.
Платон утверждал, что вообще вся “Поверхность состоит из треугольников”.
На самом деле треугольники используются везде и всюду. Уже со времён палеолита и неолита в древнем искусстве очень широко распространяются изображения равностороннего треугольника. Первобытные люди покрывали сферические сосуды сетью круглых равносторонних треугольников. Символическое изображение треугольника есть в архитектуре и строительстве (пирамиды и др.), во фрагментах одежды и украшениях. Вожди племен североамериканских индейцев носили на груди символ власти:
равносторонний треугольник. В Африке женщины туарегов также украшали себя большими пластинами из равносторонних треугольников.
А уж сколько легенд связано с Бермудским треугольником…
Скульптура невозможного треугольника, в центре бельгийской деревни Опховен

Солдаты писали письма на листочке бумаги, а затем складывали его особым образом, чтобы получился треугольник. Такие треугольники отдавали на военную почту. Они были без марок, а только с печатью полевой почты, тоже треугольной формы.
Это было не только из-за нехватки конвертов, но и из-за того, что военной цензуре было намного легче развернуть «треугольник». ( Цензура – общее название контроля власти за содержанием и распространением информации, в некоторых случаях также частной переписки, с целью ограничения либо недопущения распространения идей и сведений, признаваемых вредными или нежелательными).
Конверт-треугольник — обычно тетрадный лист бумаги, сначала загнутый справа налево, потом слева направо. Оставшаяся полоса бумаги (поскольку тетрадь не квадратной, а прямоугольной формы) вставлялась, как клапан, внутрь треугольника. Готовое к отправке письмо не заклеивалось — его всё равно должна была прочитать цензура; почтовая марка была не нужна, адрес писался на наружной стороне листа.
При отсутствии конвертов в зоне боевых действий во время Первой чеченской кампании (1994—1996) солдаты, проходившие военную службу по призыву, также иногда посылали домой письма, сложенные «треугольником». [
- А знаете ли вы, что в городе Волгограде стоит памятник солдатскому треугольнику?


Учитель: Я рассказала Вам лишь маленькую часть того, где встречаются треугольники в жизни.
Учащимся предлагается дома восстановить полностью доказательство теоремы, предлагаемое автором учебника по математике для 6 класса Дорофеева Г.В. Это задание для желающих. На перемене у учителя можно получить рисунок к этому способу доказательства. Этот рисунок демонстрируется и на слайде.

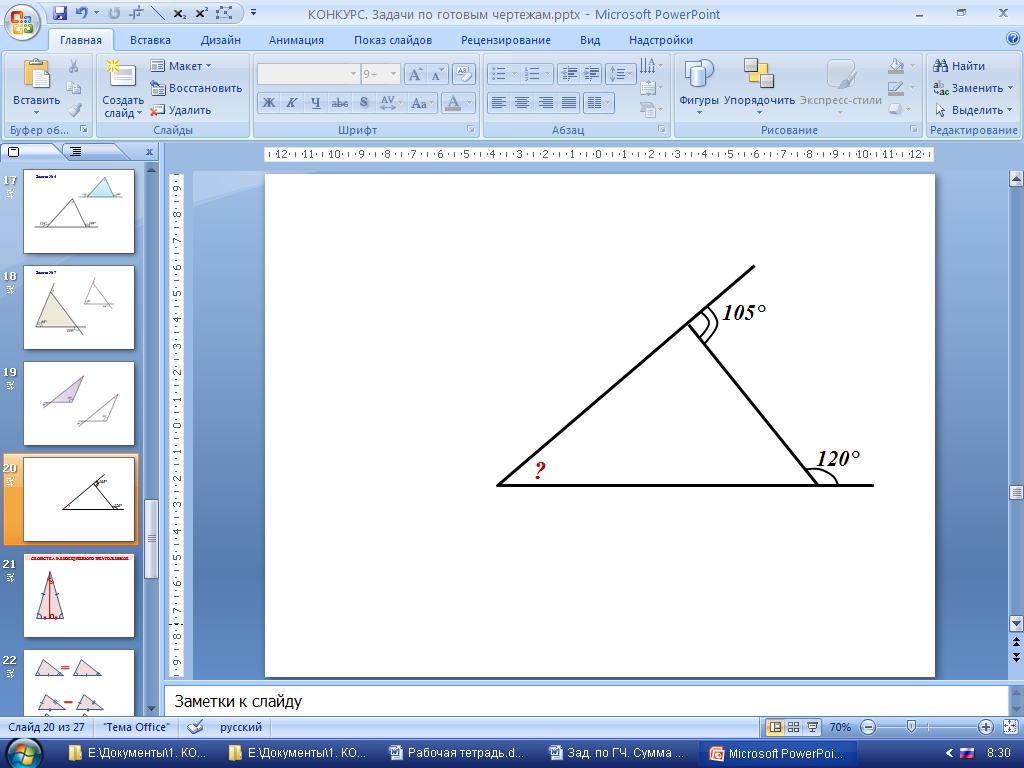
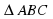 . Р=24см.
. Р=24см.