Верхне-Гуторовский филиал МБОУ «Полевской лицей»
Курского района Курской области
ТЕМА УРОКА:
СУММА УГЛОВ ТРЕУГОЛЬНИКА
Урок по геометрии в 7 классе
(1час)
Подготовила учитель
математики
Верхне-Гуторовского филиала
МБОУ «Полевской лицей»
Алтухова Л.Н.
2013-2014 уч.год
Урок геометрии по теме: "Сумма углов треугольника" . 7-й класс
Тема урока: “Сумма углов треугольника”.
Тип урока: изучение нового материала.
Цели:
Образовательные: повторить и обобщить знания о треугольнике; доказать теорему о сумме углов треугольника и классифицировать треугольники по углам и сторонам; научиться применять полученные знания при решении задач.
Развивающие: развивать геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, умение самостоятельно добывать знания.
Воспитательные: развивать личностные качества учащихся, таких как целеустремленность, настойчивость, аккуратность, умение работать в коллективе; содействовать формированию активной жизненной позиции учащихся.
Ход урока:
Начало урока. Организационный момент. (Слайд 4)
Учитель. Добрый день, ребята! Наш урок хочется начать со слов великого русского поэта А.С. Пушкин «Вдохновение нужно в геометрии,
как в поэзии»
(Учитель держит в руках треугольник) И сегодня мы с вами поговорим о треугольнике, который вдохновлял многих ученых на новые открытия и исследования Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о геометрии треугольника как о самостоятельном разделе геометрии.
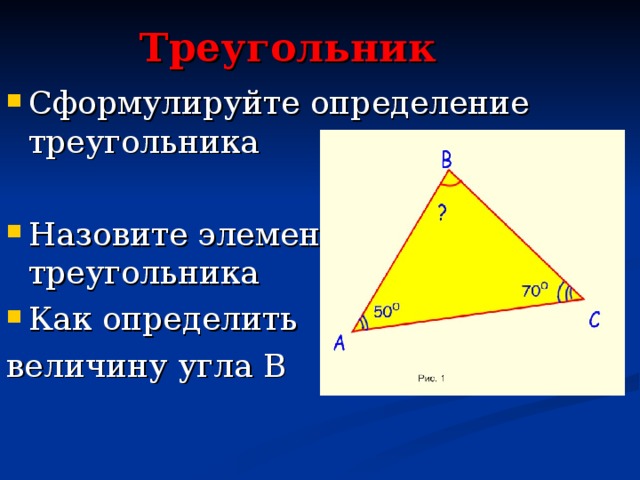
Итак, давайте вспомним, что же такое треугольник? (треугольник - это фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.) (Слайд 5)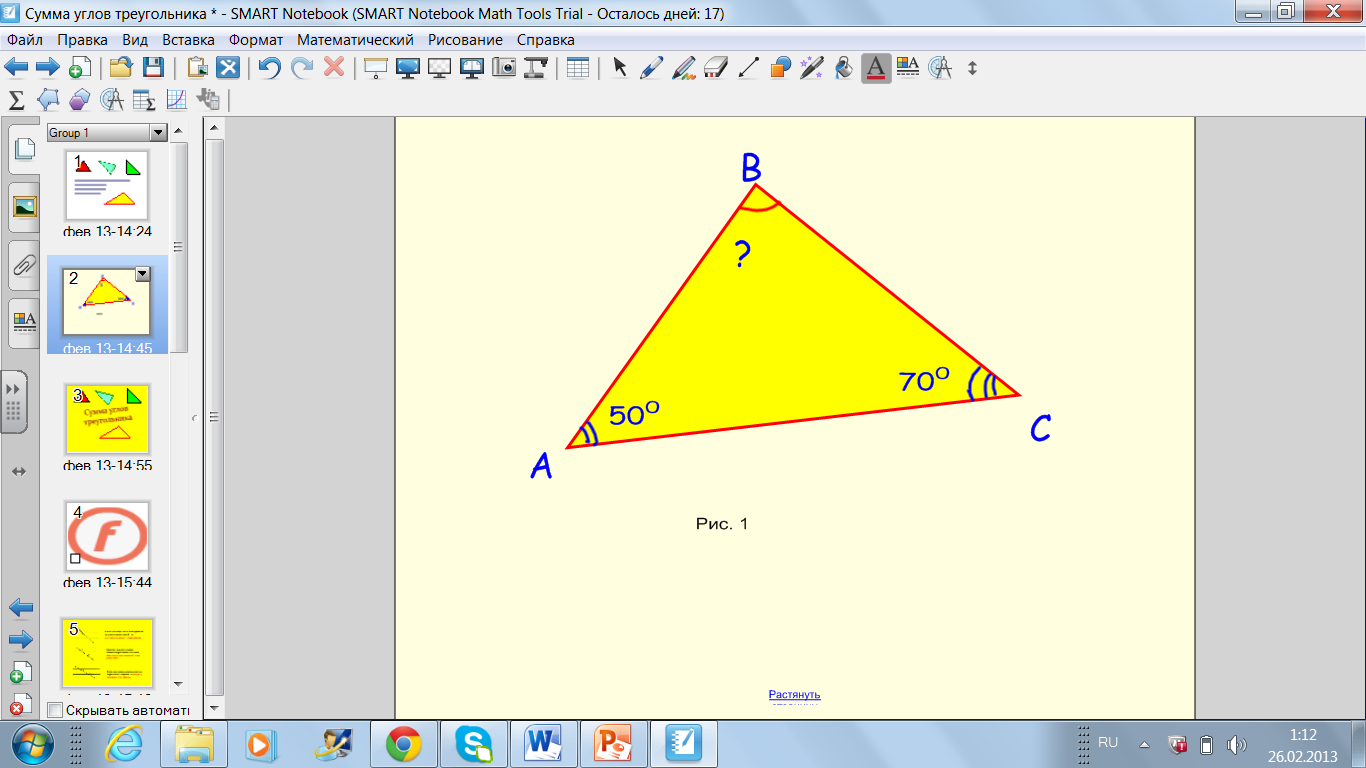 
Посмотрите на треугольник (рис. 1). Чему равен
В? (постановка проблемы)
Так вот сегодня на уроке мы попробуем с вами сформулировать и доказать замечательное свойство треугольника, которое нам поможет ответить на данный вопрос.
2. Практическая работа (способствует актуализации знаний и навыков самопознания).
Учитель. У каждого из вас есть на парте треугольники. Предлагаю провести измерения углов с помощью транспортира и найти их сумму. Результаты запишите в тетрадь (заслушать полученные ответы). Выясняем, что сумма углов у всех обучающихся получилась разная (так может получиться, потому что неточно приложили транспортир, небрежно выполнили подсчет и т.д.).
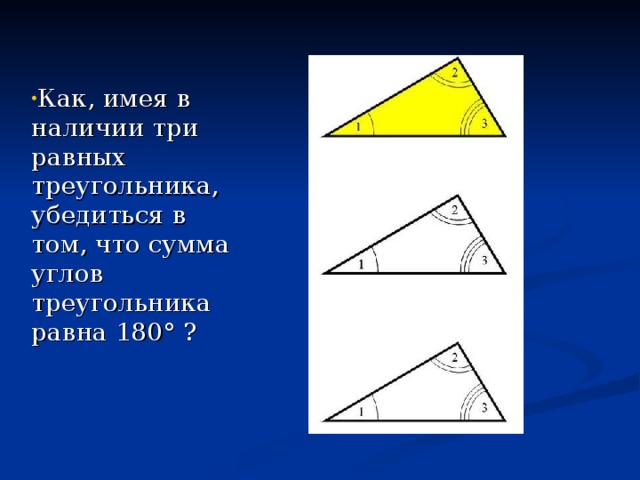
Учитель. Давайте посмотрим, как еще можно увидеть, что сумма углов треугольника равна 180 градусов. (работа с моделями на партах и на доске). (Слайды 6 и 7)
(На каждой парте лежат по 3 равных треугольника).
Учитель. Перед вами на столе три равных треугольника. Как можно в этом убедиться? Наложите один треугольник на другой, и вы проверите это.
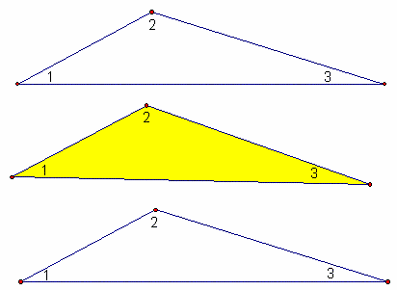
Положите цветной треугольник на стол, а два других треугольника положите рядом с первым таким образом, чтобы у одной вершины оказалось три разных угла, а стороны их совпадали.
Учитель помогает учащимся, а затем выполняет указанные действия на доске (треугольники крепятся при помощи магнитов).
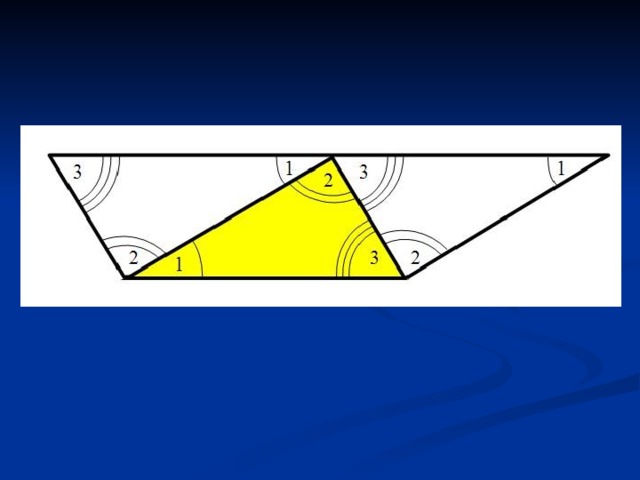
Посмотрите внимательно, что у вас получилось? Как называется угол, который составляют вместе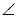 
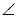1, 2 и 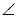3? Какова градусная мера этого угла? Значит, чему равна сумма углов 1, 2 и 3? Чему равна сумма равных им углов цветного треугольника?
Какой теперь мы можем сделать вывод о сумме углов треугольника?
Итак, мы выяснили практическим путем, что сумма углов треугольника равна 1800.
Какие утверждения, связанные с величиной – 180°, вам известны?
Развернутый угол равен 180°.
Сумма смежных углов равна 180°.
Сумма односторонних углов при параллельных прямых равна 180°.
Сумма углов треугольника равна 180°.
3. Изучение нового материала
Формулировка и доказательство теоремы.
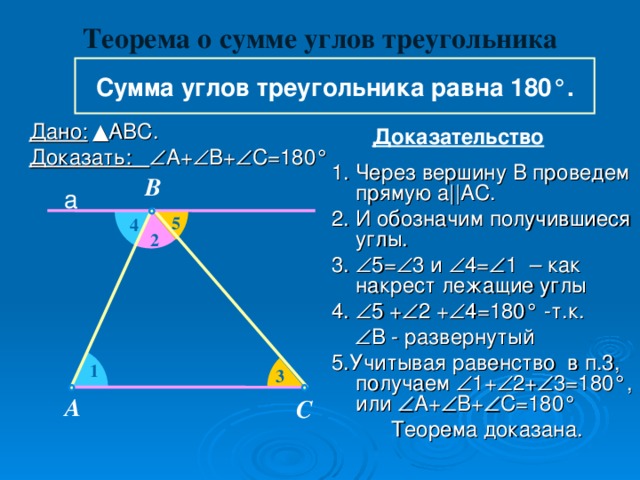
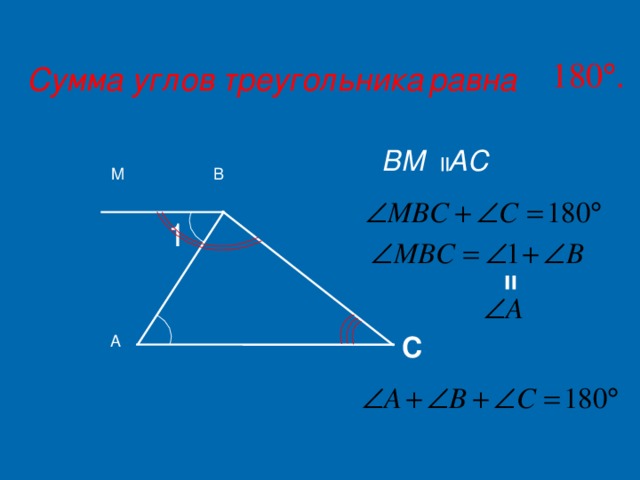
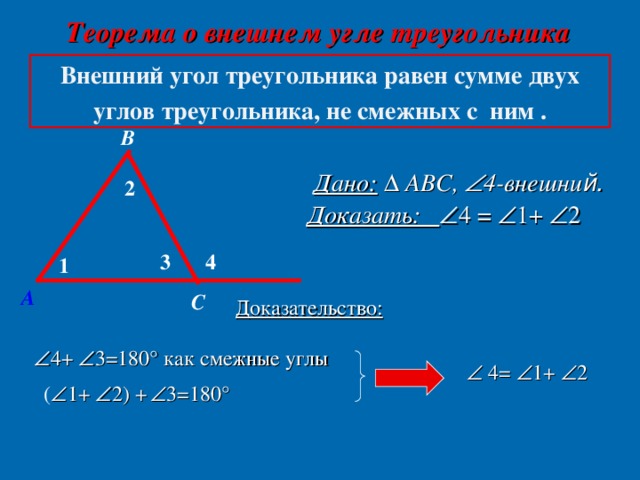
Учитель. Проведем доказательство теоремы. (Учащиеся записывают доказательство в тетрадь).Давайте посмотрим на следующий рисунок.(Слайд 8,9)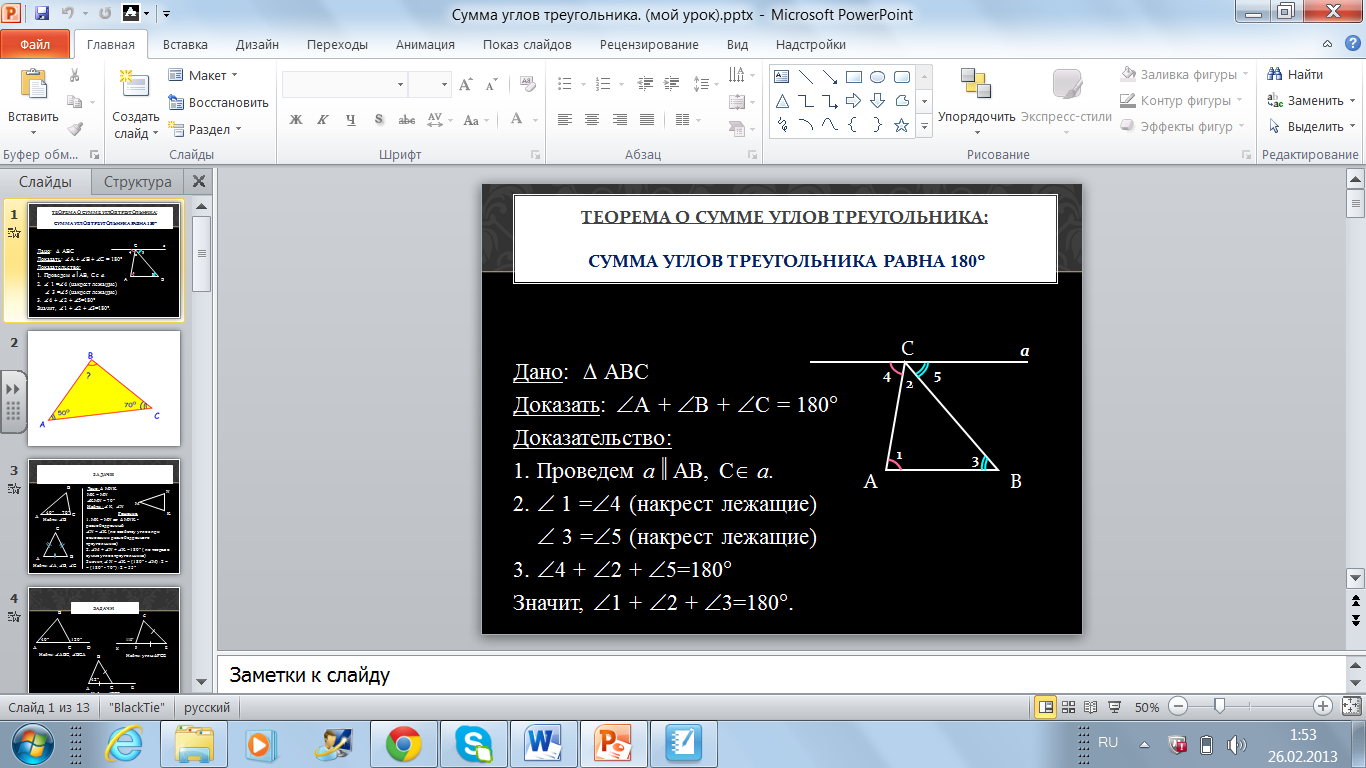
Учитель. Нам дан треугольник АВС, проведем через вершину В прямую а, параллельную стороне АС. Какими будут углы 1 и 4? Углы 3 и 5?
Обучающиеся поясняют, что они равны как накрест лежащие.
Учитель. Итак мы получили: 1 = 4, 5 = 3,4 + 2 + 5 = 180 ° (так как в сумме они дают развернутый угол). Значит, 1 + 2 + 3= 180°.
Вывод: сумма углов треугольника равна 180 градусов. (Вывод могут сделать сами обучающиеся).
Оформить доказательство теоремы в тетрадях.
Доказать: А +В + С = 180º
Доказательство:
Проведем, а | | АС.
4= 1 (накрест лежащие) 5= 3 (накрест лежащие)
4 + 2 + 5 = 180º.
Значит, 1 +2 + 3 = 180º . т. д.
Повторяем план доказательства:
Провести прямую через одну из вершин | | противолежащей стороне.
Составить пары равных углов.
Представить развёрнутый угол в виде суммы.
Заменить слагаемое равным им углам треугольника.
Учитель. Ребята, можете вы сформулировать теорему о сумме углов треугольника?
Формулировка теоремы обучающимися.
Теперь вы можете дать ответ на вопрос, поставленный в начале урока. Посмотрите на треугольник (рис. 1). Чему равенВ? (Ответ: 60º)(Слайд 5)
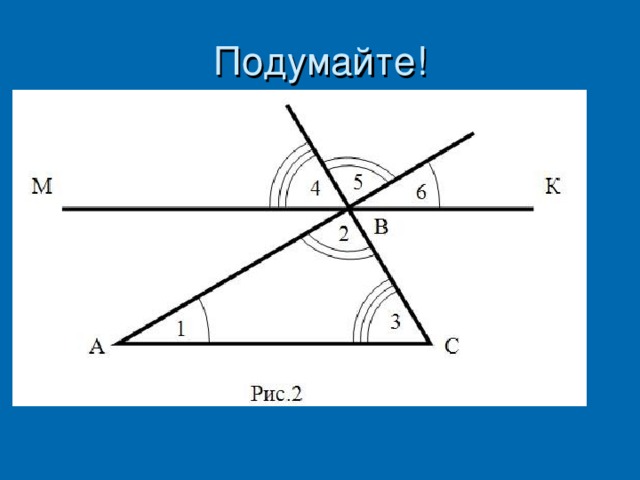
Учитель. Возможны другие случаи доказательства теоремы о сумме углов треугольника (Слайд 10,11) Доказательства рассматриваются устно.
Закрепление.
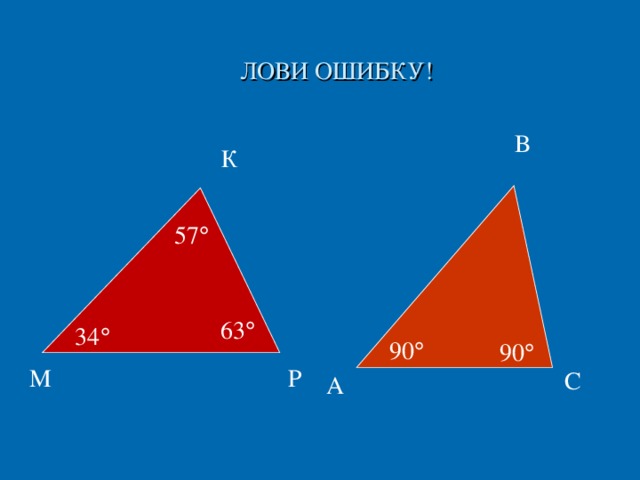
Лови ошибку! Что не так на рисунках? (Слайд 12)
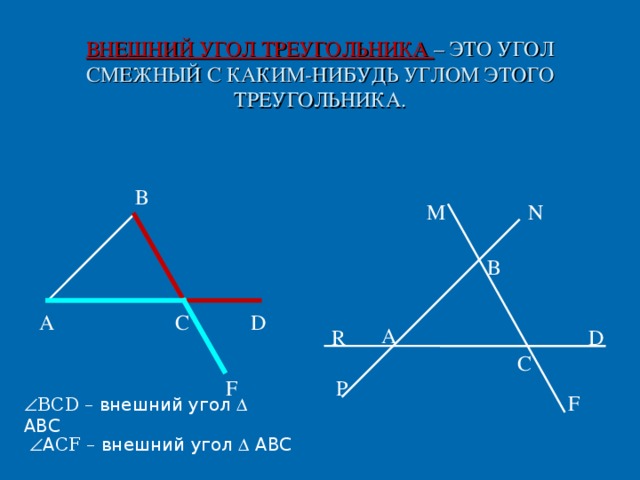
Введение нового понятия. )(Слайд 13,14,15)
Учитель. Посмотрите на рисунок. Какими будут углы АСВ и ВСD?
Да, они смежные. Так вот, угол, смежный с каким-нибудь углом треугольника, называется внешним углом треугольника. Значит угол ВСD – внешний угол треугольника.
Ответьте на вопросы:- Какой угол называется внешним углом треугольника?
- Каким свойством обладает внешний угол треугольника? (Внешний угол треугольника равен сумме двух углов, не смежных с ним).
Дома вы самостоятельно оформите доказательство свойства внешнего угла треугольника в тетради.
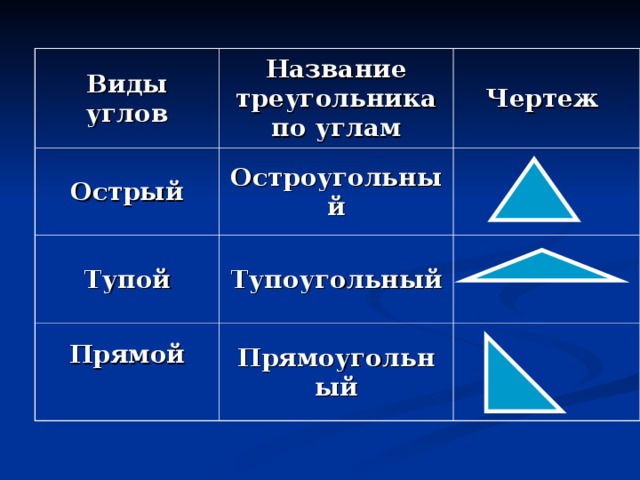
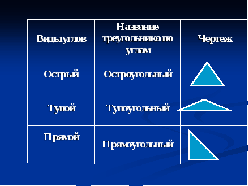
Учитель. Теорема о сумме углов треугольника позволяет классифицировать треугольники не только по сторонам, но и по углам. (Слайд 16)
4. Физкультминутка. Ученики выполняют гимнастику для глаз.
Закрепление пройденного материала.
Устный тест (Слайд 17)
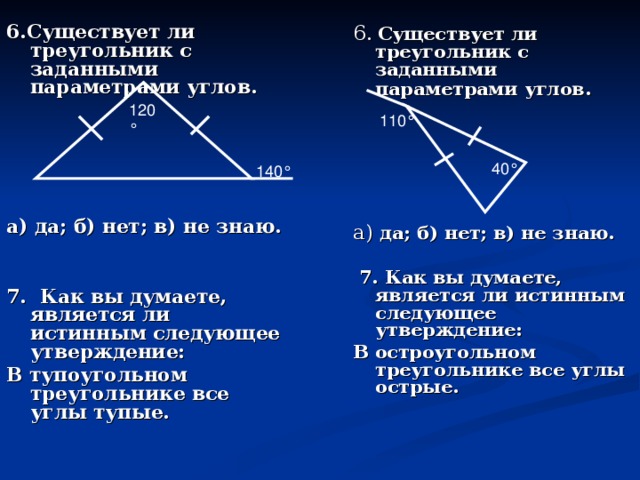
1. В треугольнике АВС угол А равен 90°, при этом другие два угла:
а) один острый, а другой может быть
прямым;
б) оба острые;
в) один острый, а другой может быть
тупым .
2. В треугольнике АВС угол В - тупой, при этом другие два угла могут быть:
а) только острыми;
б) острый и прямой;
в) острый и тупой.
3. В остроугольном треугольнике могут быть:
а) все углы острые;
б) один тупой угол;
в) один прямой угол.
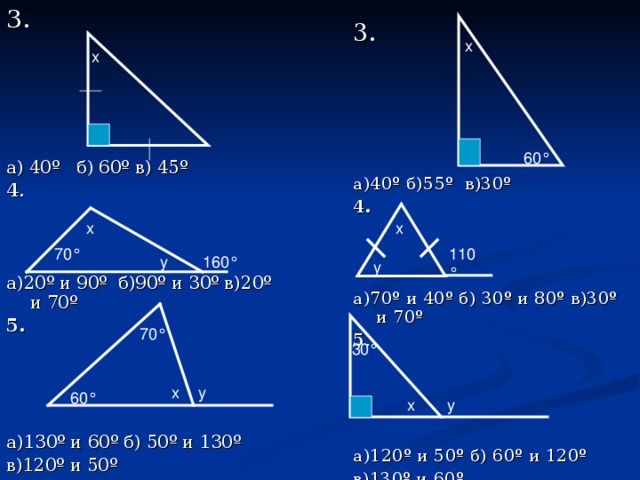
Учитель предлагает обучающимся устно решить задачи по готовым чертежам (Слайд 24-29)
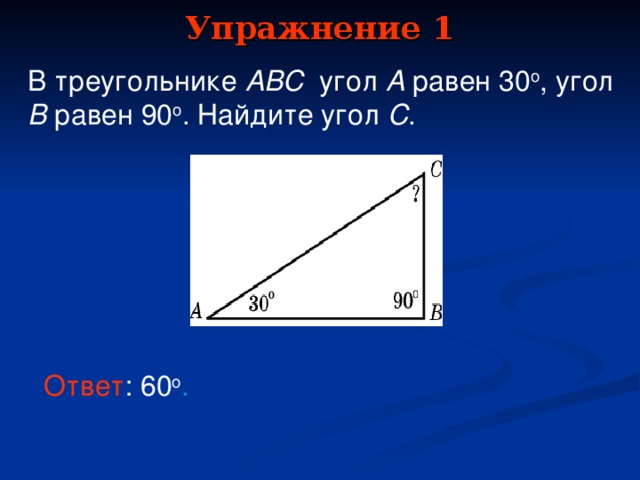
В треугольнике ABC угол A равен 30o, угол B равен 90o. Найдите угол C.(60)
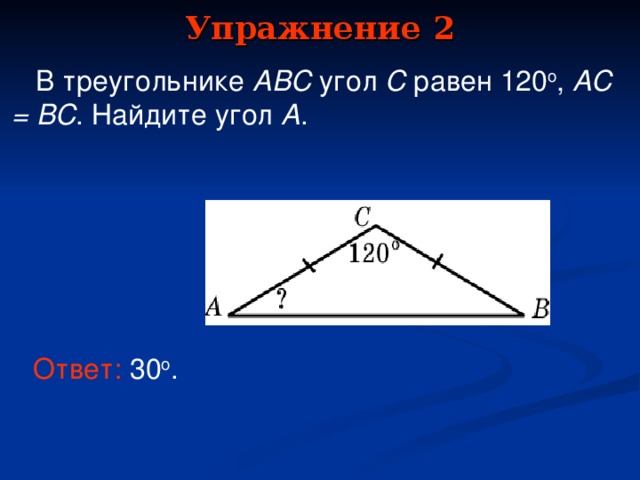
В треугольнике ABC угол C равен 120o, AC = BC. Найдите угол A.(30)
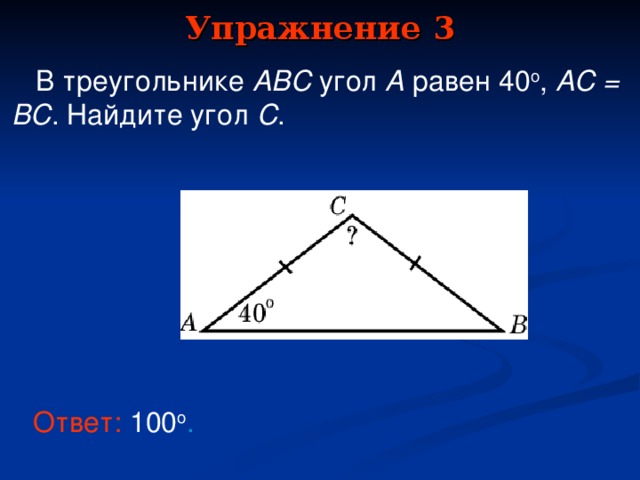
В треугольнике ABC угол A равен 40o, AC = BC. Найдите угол C.(100)
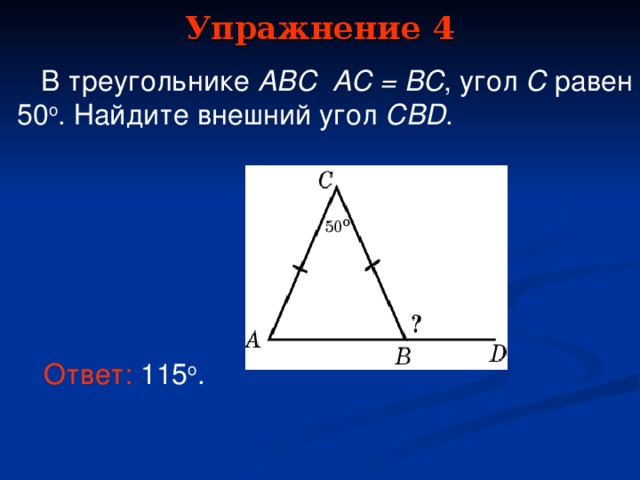
В треугольнике ABC AC = BC, угол C равен 50o. Найдите внешний угол CBD. (115)
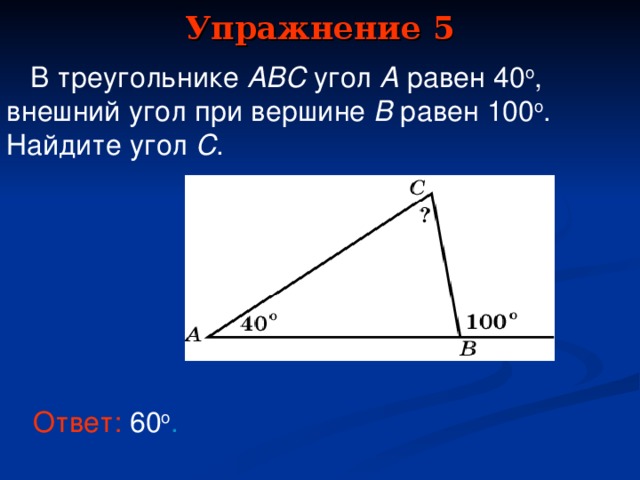
В треугольнике ABC угол A равен 40o, внешний угол при вершине B равен 100o. Найдите угол C. (60)
В треугольнике ABC AB = BC. Внешний угол при вершине B равен 140o. Найдите угол C.(70)
Учитель. Задачи №7 и №8 обучающиеся выполняют у доски (Слайд 30,31)
Углы треугольника относятся как 1:2:3. Найдите меньший из них.(30)
Для черепичных крыш угол между двумя стропилами берут равным приближённо 90º. Определите, какой высоты будет крыша, если ширина дома 10 м? (5м)
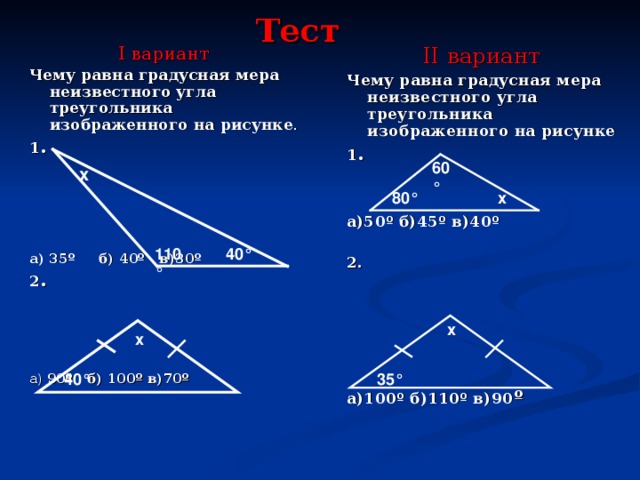
Тестирование (Слайд 32-34)
Проверка (Слайд 35)
Домашнее задание (Слайд 36) П.30,31 № 224,228, оформите доказательство свойства внешнего угла треугольника в тетради.
Итог урока:
Что нового узнали на сегодняшнем уроке?
С какими видами треугольника познакомились?
Какая работа вам понравилась больше всего?
Какие задания вызвали затруднения?
Был ли урок интересным?
Итак, ребята этот урок пополнил ваши знания о треугольнике, но это еще не предел. На следующих уроках мы продолжим изучение треугольников, и вы узнаете еще много интересного и познавательного об этой геометрической фигуре.
С одной стороны треугольник – это геометрическая фигура, с другой стороны треугольник это - тайный оккультный знак, встречающийся во многих цивилизациях. Три угла, три грани - магическое число 3. Не удивительно, что треугольник можно найти на тайных письменах, символах, пентаграммах. И совсем не удивительно, что самые загадочные места и строения могут быть связаны тоже с треугольниками. Например, египетские пирамиды (в Египте треугольник символизировал триаду духовной воли, любви-интуиции и высшего разума человека, то есть его личность и душу.) Или звезда Давида (еврейский символ, образованный наложением двух треугольников). А еще Бермудский треугольник.
Использованная литература:
Геометрия. 7-9 класс./ Л.С.Атанасян, В.Ф.Бутузов и др. Москва: Просвещение, 2012
Универсальные поурочные разработки по геометрии. 7 класс/ Н.Ф.Гаврилова Москва. «ВАКО». 2013
7 класс Геометрия. Поурочные планы. / Т.Л.Афанасьева, Л.А.Тапилина. Волгоград: Учитель, 2006.
