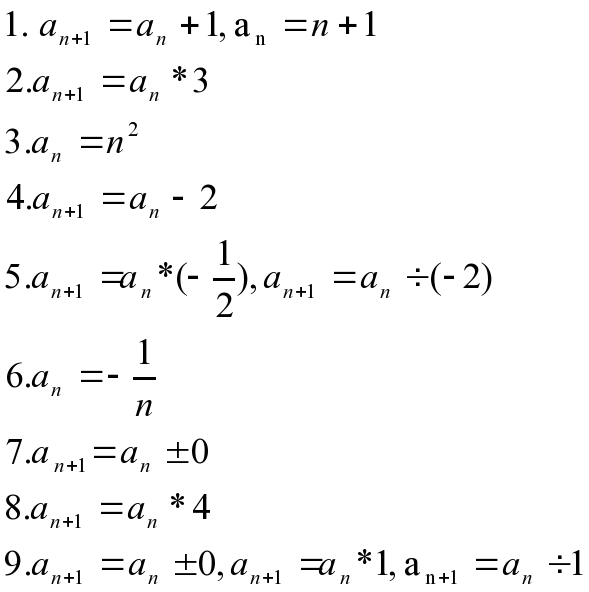Конспект урока алгебры.
Алгебра. 8 класс. Задачник для учащихся общеобразовательных учреждений [А.Г.Мордкович и др.]; под ред. А.Г.Мордковича. – М.: Мнемозина, 2009.
1. Мотивационно-ориентировочный этап – 10 мин
2. Содержательный этап – 30 мин
3. Рефлексивно-оценочный этап – 5 мин
| Деятельность учителя | Деятельность учащихся |
Мотивационно-ориентировочный этап |
| Здравствуйте, ребята! Я очень рад вас видеть! Сегодня на уроке мы окунемся в удивительный мир математики и, как всегда, узнаем что-то новое. |
|
| Актуализация: На доске записаны следующие числовые последовательности: 1, 2, 3, 4, 5,… 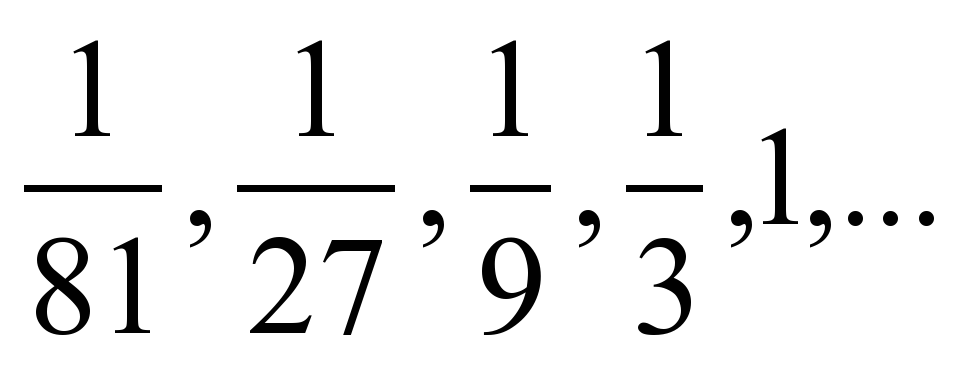 4, 9, 16, 25, 36, … 5, 3, 1, -1, -3, … -32, 16, -8, 4, -2, … 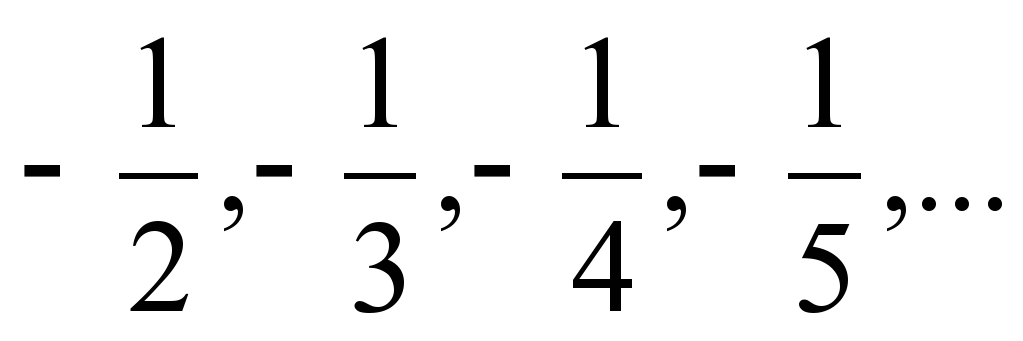 
0, 0, 0, 0, 0, … 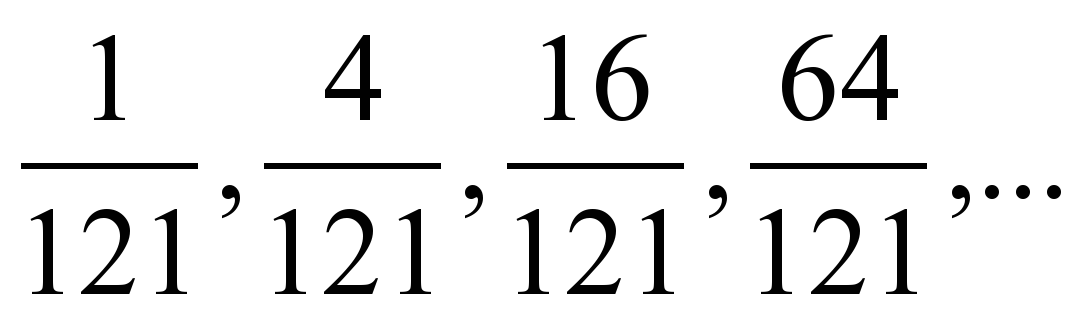
1, 1, 1, 1,… |
| На прошлом уроке вы изучали тему «Числовая последовательность». Какие способы задания числовой последовательности вы знаете? | Рекуррентный и формулой n-го члена. |
| Какой способ задания последовательности называется рекуррентным? | Рекуррентный – способ задания последовательности, при котором вычисление (n+1)-го члена последовательности производится через предыдущие n членов. |
| На доске записаны числовые последовательности. Запишите для каждой из них, какой формулой она задана: 1, 2, 3, 4, 5,… 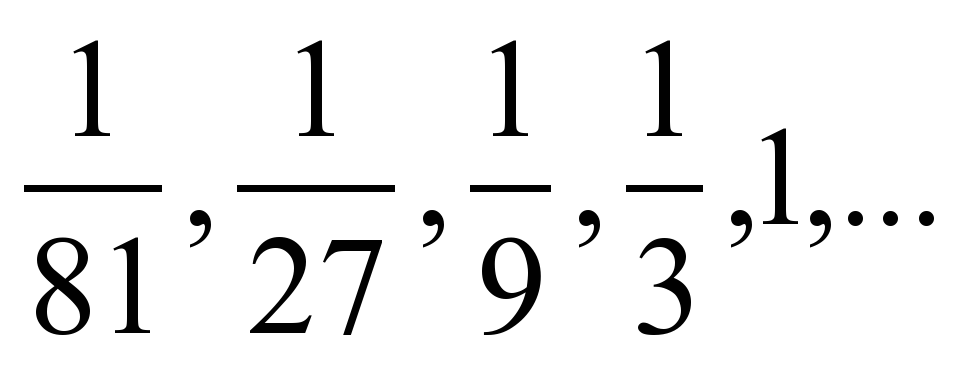
1, 4, 9, 16, 25, … 5, 3, 1, -1, -3, … -32, 16, -8, 4, -2, … 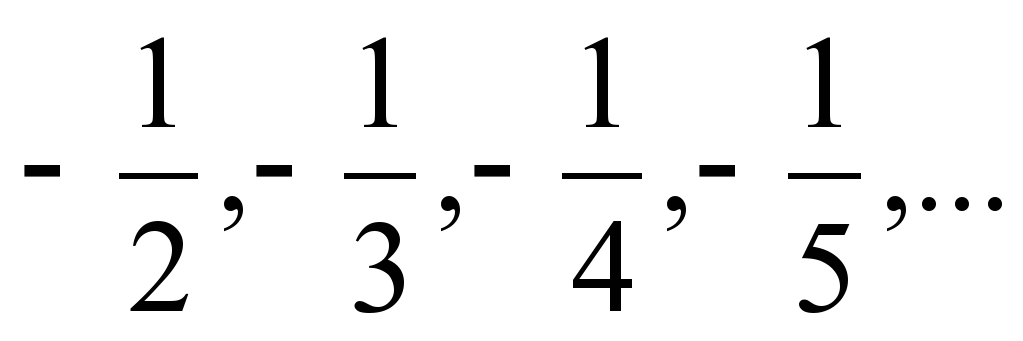 
0, 0, 0, 0, 0, … 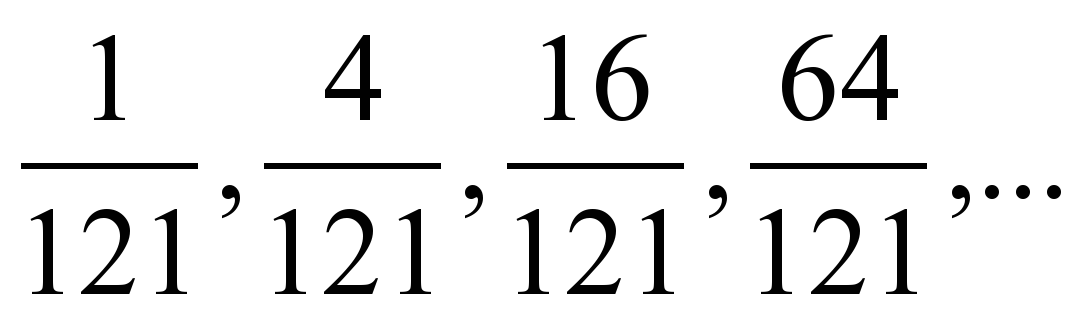
1, 1, 1, 1,… |
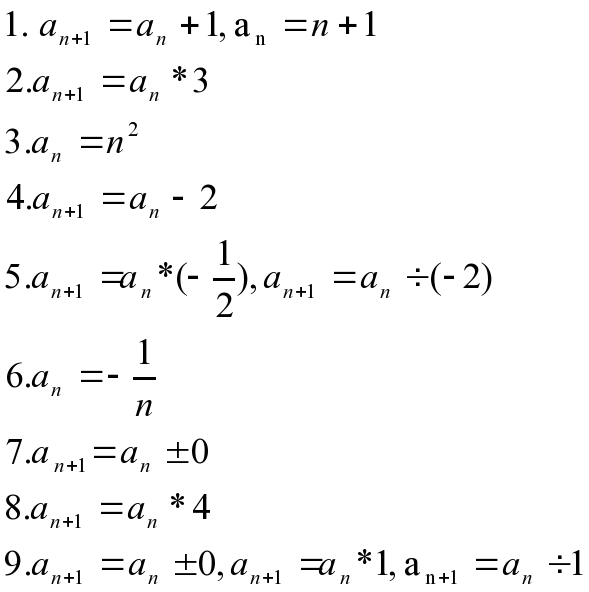
|
| Какие из данных числовых последовательностей заданы рекуррентной формулой, а какие формулой n-го члена? | Рекуррентной формулой: 1, 2, 4, 5, 7, 8, 9. Формулой n-го члена: 1, 3, 6. |
| Рассмотрим последовательности, заданные рекуррентной формулой. Как в первой последовательности связаны an и an+1 члены? | an+1 получается прибавлением к an единицы. |
| Как в четвертой последовательности связаны an и an+1 члены? | an+1 получается вычитанием из an двух. |
| Иначе говоря, an+1 получается прибавлением к an минус двух. |
|
| Как в седьмой последовательности связаны an и an+1 члены? | an+1 получается прибавлением или вычитанием из an нуля. |
| Как в девятой последовательности связаны an и an+1 члены? | an+1 получается прибавлением или вычитанием из an нуля. Или an+1 получается умножением или делением an на единицу. |
| Что объединяет эти последовательности? Как находится последующий член через предыдущий? | Последующий член получается из предыдущего прибавлением (вычитанием) одного и того же числа. |
| Рассмотрим остальные последовательности, которые заданы рекуррентной формулой. Как в них связаны последующий член и предыдущий? | Во второй последовательности an+1 получается умножением an на три. В пятой последовательности an+1 получается умножением an на минус одну вторую или делением на минус два. В восьмой последовательности an+1 получается умножением an на четыре. В девятой последовательности an+1 получается умножением или делением an на единицу. |
| Как в этих последовательностях находится последующий член через предыдущий? | Последующий член получается из предыдущего умножением (делением) на одно и то же число. |
| Итак, мы разделили записанные на доске последовательности на три группы: - те, в которых последующий член получается из предыдущего прибавлением одного и того же числа; - те, в которых последующий член получается из предыдущего умножением на одно и то же число; - заданные формулой n-го члена. На сегодняшнем уроке и в дальнейшем мы будем изучать последовательности первых двух групп. |
|
| Мотивация |
| Не только в математике, но и на практике в жизни часто встречаются задачи, для решения которых используются такие последовательности, то есть последовательности, в которых каждый член равен предыдущему, сложенному с одним и тем же числом, либо умноженному на одно и тоже число. Рассмотрим задачу: продолжительность года приблизительно равна 365 суткам. Более точное значение равно 365¼ суток, поэтому каждые четыре года накапливается погрешность, равная одним суткам. Для учета этой погрешности к каждому четвертому году добавляются сутки, и удлиненный год называется високосным. Например, в третьем тысячелетии високосными годами будут годы 2016, 2020, 2024, 2028, 2032… Какая зависимость существует между последующим и предыдущим членами этой последовательности? | В этой последовательности каждый ее член, начиная со второго, равен предыдущему, сложенного с одним и тем же числом 4. То есть an+1=an+4, где a1=2016
|
| Рассмотрим следующую задачу: Рассмотрим равносторонний треугольник со стороной 4 см. Построим треугольник, вершинами которого являются середины сторон данного треугольника. По свойству средней линии треугольника сторона второго треугольника равна 2 см. Продолжая аналогичные построения, получим треугольники со сторонами 1, ½, ¼ см и т.д. Запишем последовательность длин сторон этих треугольников: 4, 2, 1, ½, ¼, … 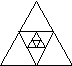
Какая зависимость существует между последующим и предыдущим членами этой последовательности? | В этой последовательности каждый ее член, начиная со второго, равен предыдущему, умноженному на одно и то же число ½. То есть bn= ½ּ bn.. |
| Действительно, в практических задачах часто встречаются выделенные нами первые две группы последовательностей. Поэтому мы будем изучать последовательности этих групп. |
|
| Постановка учебной задачи |
| И сегодня целью нашего урока является изучить эти последовательности: дать им названия, сформулировать определения и изучить их свойства. |
|
| II. Содержательный этап |
| Сначала будем рассматривать последовательности первой группы и заполнять первый столбец канвы-таблицы. В таких последовательностях каждый член получается из предыдущего, прибавлением к нему одного и того же числа. Это можно записать рекуррентной формулой: an+1=an+d, где d – некоторое число. Запишем это в канву-таблицу. | an+1=an+d, где d – некоторое число |
| Выразите из этой формулы число d. Запишем это в канву-таблицу. | d= an+1-an |
| Чему оно равно?
| Разности двух соседних членов последовательности. |
| Поэтому d называют разностью. Отметьте это у себя в таблицах. | d= an+1-an - разность |
| Рассмотрим пример: Продолжите ряд: -10, -14, -18… Чему равно d? | d=-4 -10, -14, -18, -22, -26, -30, … |
| Обратимся к примерам, рассмотренным в начале урока. Чему равно d в последовательностях 1, 4, 7, 9? | 1. d=1 4. d=-2 7. d=0 9. d=0 |
| Чему равны первый, второй и третий члены последовательности 4? | a1=5, a2=3, a3=1 |
| Как можно получить 3 из 5 и 1?
| 3 = (5+1)/2, то есть 3 – это среднее арифметическое чисел 5 и 1. |
| Таким свойством обладают любые три подряд идущие члена этой последовательности, начиная со второго. Давайте запишем это свойство в общем виде. Если один из членов этой последовательности an, то какой для него будет предыдущим членом, а какой последующим? | an+1 – последующий для an an-1 – предыдущий для an |
| Тогда получили три подряд идущих члена последовательности an-1, an, an+1. Как выразить an через два других члена? | 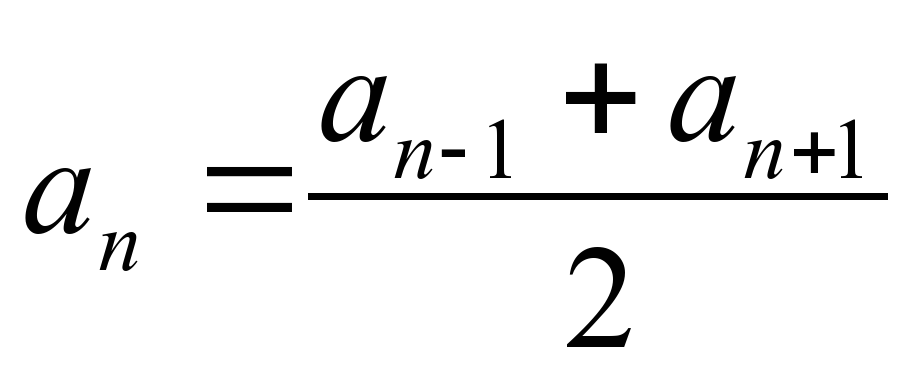 |
| Как вы думаете, почему первый член последовательности таким свойством не обладает? | Для него нет предыдущего. |
| Какое тогда условие накладывается на n в формуле? | 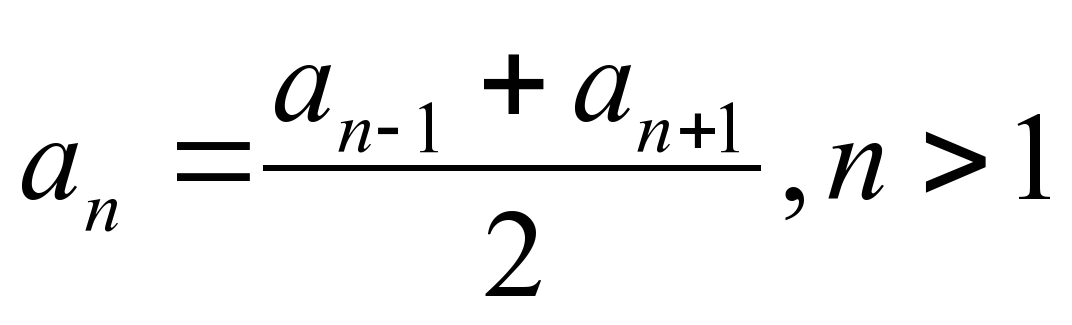 |
| Таким образом, an член этой последовательности есть среднее арифметическое его последующего и предыдущего членов. Поэтому данный вид последовательности получил название арифметическая прогрессия. Запишем заголовок первого столбца канвы таблицы «Арифметическая прогрессия» и название числовой последовательности в определении. | Заполняют заголовок первого столбца таблицы, полностью записывают определение арифметической прогрессии. |
| Полученная связь между членами арифметической прогрессии является ее свойством. Сформулируйте его и запишите в канву-таблицу. | Каждый член арифметической прогрессии а1, а2, а3,…,аn,…, начиная со второго, равен среднему арифметическому двух соседних с ним членов: 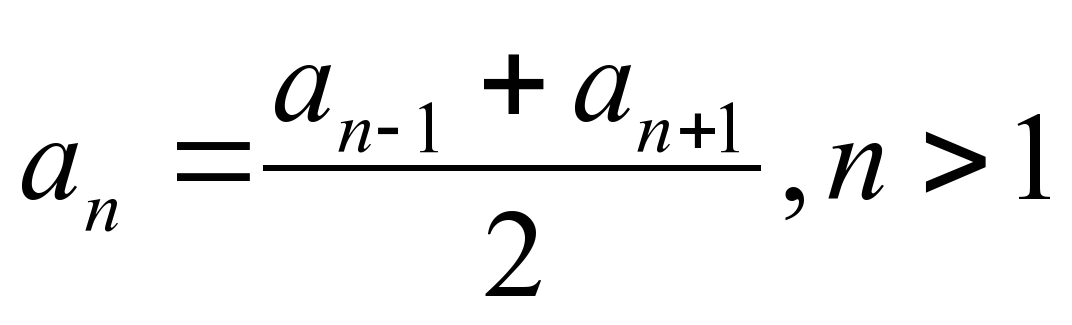 |
| Докажем это свойство. Для этого сначала запишите рекуррентную формулу для an и an+1 членов. Запишем это как первый пункт доказательства в канву-таблицу. Как вы получили данные формулы? Отметьте это в скобках. | 1). an=an-1+d an+1=an+d
Из определения арифметической прогрессии |
| Переходим ко второму пункту доказательства. Выразите из первого равенства аn-1 | 2). an-1= an- d |
| Заметим, что в формуле, которую требуется доказать, отсутствует d, а в числителе стоит сумма чисел an-1 и an+1. Как вы думаете, что нужно сделать с данными равенствами, чтобы получить искомую формулу? Запишите. | Нужно сложить эти равенства. Записывают в таблицу: 2). an-1= an- d + an+1=an+d ________ an-1+ an+1= an- d+ an+d an-1+ an+1=2* an |
| Какое еще действие нужно произвести, чтобы получить искомую формулу? | Разделить обе части равенства на 2. Записывают: an-1+ an+1=2* an 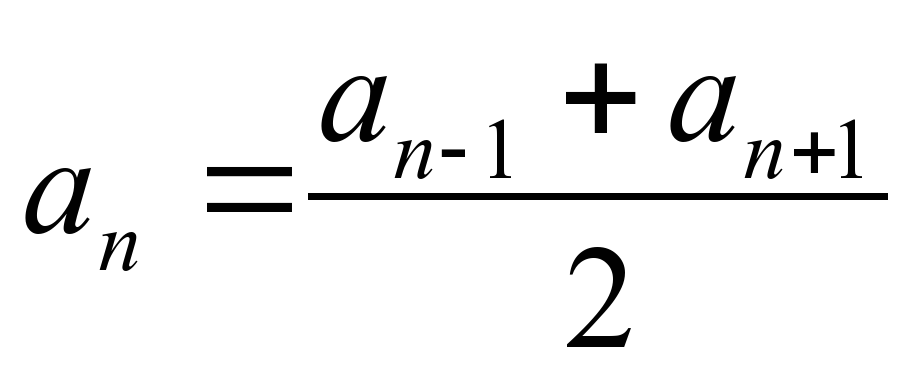 |
| Для любого ли числа n справедлива полученная формула? | Нет, только для n, больших единицы. Дописывают в канву таблицу n1. |
| Теперь рассмотрим последовательности второй группы. Определение и свойства этих последовательностей вводятся аналогично определению и свойствам последовательностей первой группы. В таких последовательностях каждый член получается из предыдущего, умножением на одно и то же число. Это можно записать рекуррентной формулой: bn+1=bn*q, где q – некоторое число. Запишем это в канву-таблицу во второй столбец. | bn+1=bn*q, где q – некоторое число |
| Выразите из этой формулы число q. Запишем это в канву-таблицу. | q= bn+1/bn |
| Всегда ли выполняется данное равенство? | Нет. |
| Почему?
| Нельзя делить на ноль, поэтому bn не может быть нулем. |
| То есть ни один из членов такой последовательности не может быть равен нулю, а значит и bn+1 не равно нулю, поэтому и q не может быть равно нулю. Запишите эти условия в канву-таблицу. | q= bn+1/bn, q≠0, bn≠0 |
| Число q называют знаменателем. Отметьте это у себя в таблицах. | q= bn+1/bn, q≠0, bn≠0 - знаменатель |
| Рассмотрим пример: Продолжите ряд: 1/5, -1, 5, … Чему равно q? | q=-5 1/5, -1, 5, -25, 125, -625… |
| Снова обратимся к примерам, рассмотренным в начале урока. Чему равно q в последовательностях 2, 5, 8, 9? | 2. q=3 5. q=-1/2 8. q=4 9. q=1 |
| Чему равны первый, второй и третий члены последовательности 8? | b1=1/121, b2=4/121, b3=16/121 |
| Как можно получить 4/121 из 1/121 и 16/121. Проведите аналогию с заполнением первого столбца. | 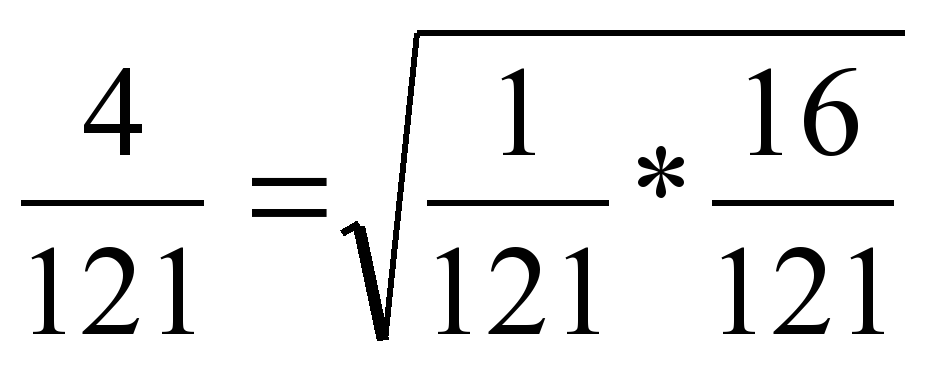 , то есть 4/121 – это среднее геометрическое чисел 1/121 и 16/121. , то есть 4/121 – это среднее геометрическое чисел 1/121 и 16/121. |
| Таким свойством обладают любые три подряд идущие члена этой последовательности, начиная со второго. Как это свойство запишется в общем виде через bn-1, bn, bn+1 ? | 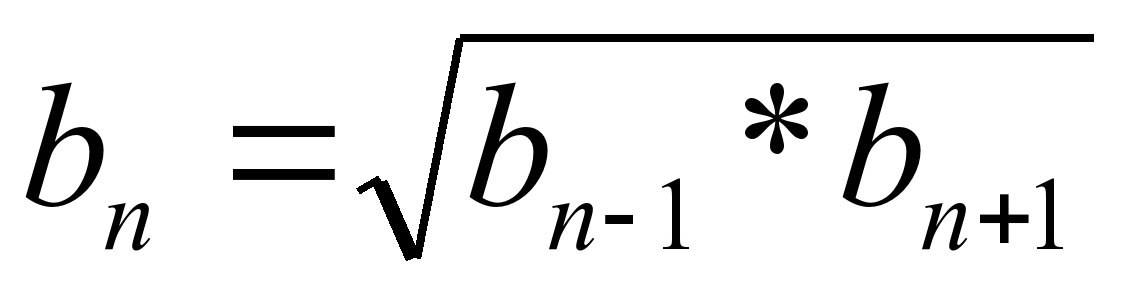 |
| Всегда ли справедлива эта формула? | Нет, только для bi0 , n1 |
| Почему? | Корень можно извлечь только из неотрицательного числа. Для первого члена последовательности нет предыдущего. |
| Какое тогда условие накладывается на bi в формуле? | 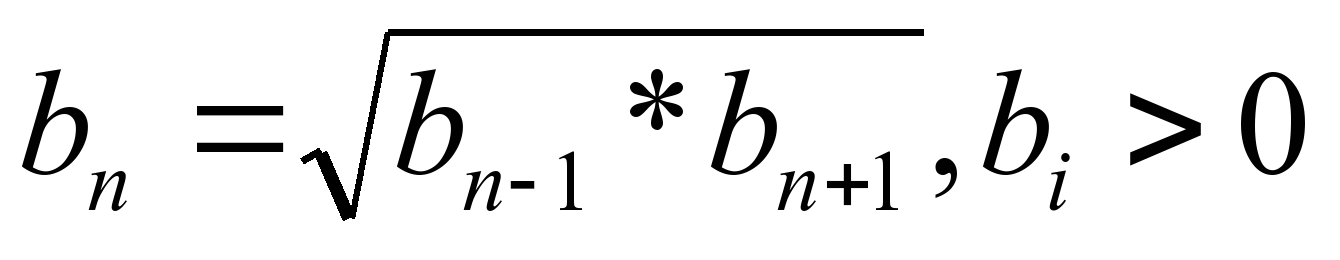 , n1 , n1 |
| Итак, bn член этой последовательности есть среднее геометрическое его последующего и предыдущего членов. Поэтому данный вид последовательности получил название геометрическая прогрессия. Запишем заголовок второго столбца канвы таблицы «Геометрическая прогрессия» и название числовой последовательности в определении. | Заполняют заголовок второго столбца таблицы, полностью записывают определение геометрической прогрессии. |
| Полученная связь между членами геометрической прогрессии, как и для арифметической, является ее свойством. Сформулируйте его и запишите в канву-таблицу. | Каждый член геометрической прогрессии b1, b2, b3,…,bn,…, начиная со второго, равен среднему геометрическому двух соседних с ним членов: 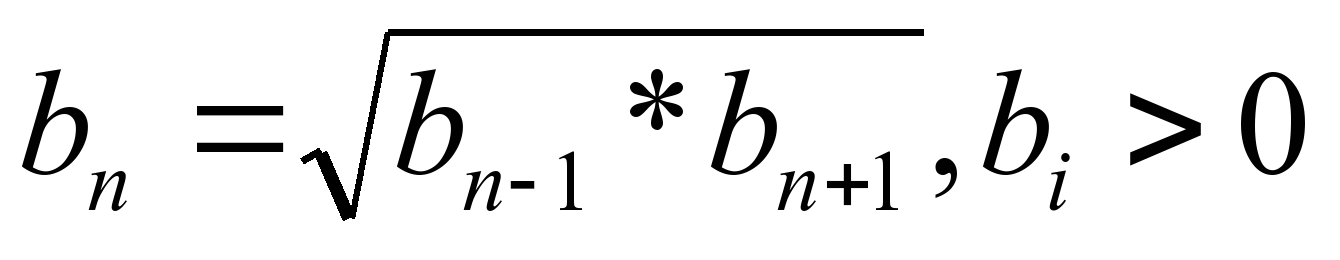 , n1 , n1 |
| Докажем это свойство аналогично свойству арифметической прогрессии. | 1). bn=bn-1*q bn+1=bn*q (из определения геометрической прогрессии) 2). bn-1= bn/q * bn+1=bn*q ________ bn-1* bn+1=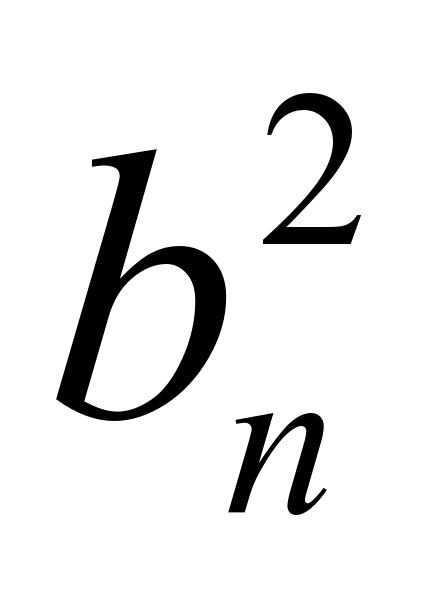 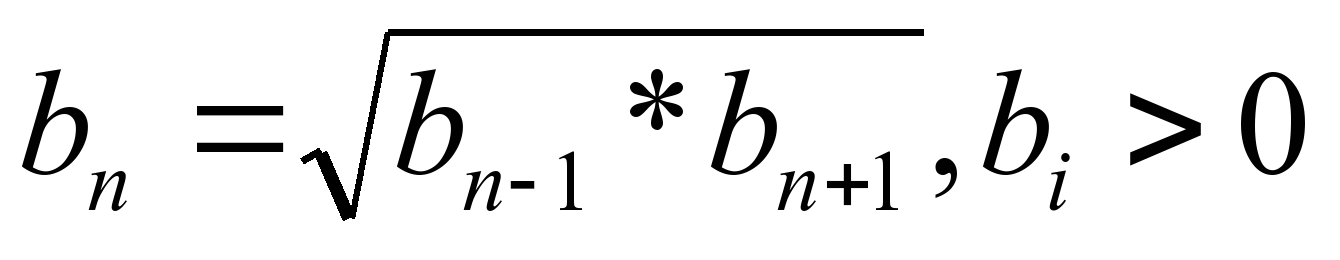 , n1 , n1 |
| Итак, для арифметической и геометрической прогрессий сформулированы аналогичные свойства. Давайте сформулируем обратные утверждения для каждого из них и посмотрим, верны они или нет. |
|
| Рассмотрим сначала свойство арифметической прогрессии. Сформулируйте для него обратное утверждение. | Если в последовательности а1, а2, а3,…,аn,…, каждый член, начиная со второго, равен среднему арифметическому двух соседних с ним членов: 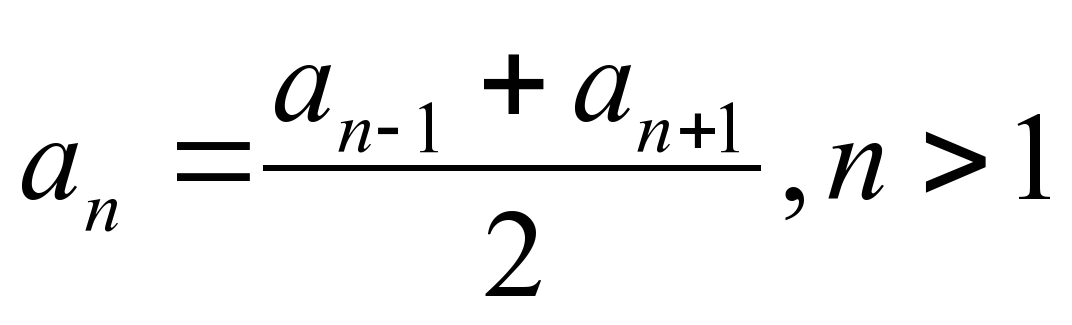 , , то такая последовательность является арифметической прогрессией. |
| Как вы думаете, будет ли это утверждение верным? | Наверное, да. |
| Действительно, равенство an-1+ an+1=2*an можно переписать в виде an-an-1= an+1 - аn, что означает, что разность между любым членом последовательности и предшествующим ему всегда одна и та же, а это означает, что задана арифметическая прогрессия. Таким образом, сформулирован признак арифметической прогрессии, запишите его в таблицу. | Записывают в первый столбец: Если в последовательности а1, а2, а3,…,аn,…, каждый член, начиная со второго, равен среднему арифметическому двух соседних с ним членов: 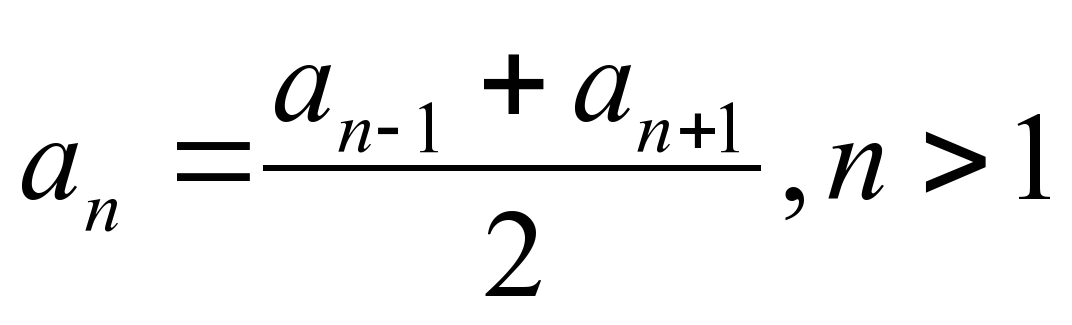 , , то такая последовательность является арифметической прогрессией.
|
| Теперь рассмотрим свойство геометрической прогрессии. Сформулируйте для него обратное утверждение. | Если в последовательности b1, b2, b3,…,bn,…, каждый член, начиная со второго, равен среднему геометрическому двух соседних с ним членов: 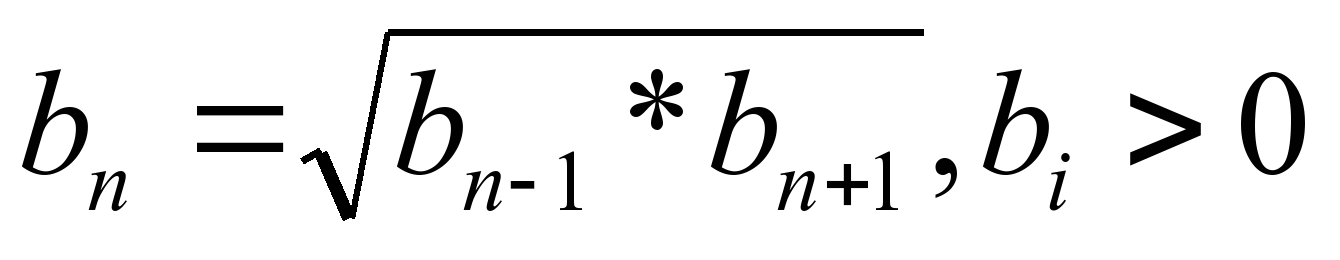 , n1 , n1 то такая последовательность является геометрической прогрессией. |
| Как вы думаете, будет ли это утверждение верным? | Наверное, да. |
| Действительно, равенство bn-1* bn+1=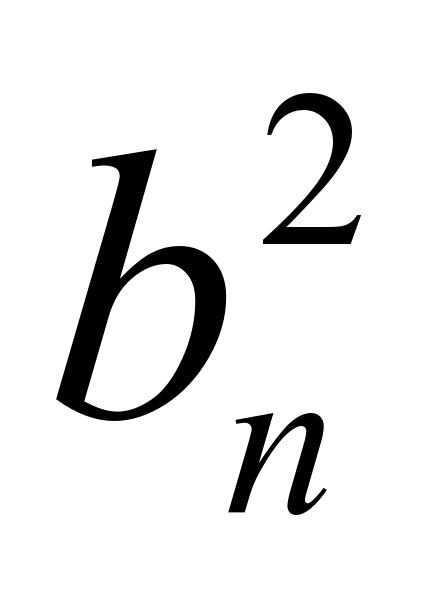 можно переписать в виде bn/bn-1= bn+1/bn, что означает, что отношение любого члена последовательности к предшествующему ему всегда одно и то же, а это означает, что задана геометрическая прогрессии. Таким образом, сформулирован признак геометрической прогрессии, запишите его в таблицу. можно переписать в виде bn/bn-1= bn+1/bn, что означает, что отношение любого члена последовательности к предшествующему ему всегда одно и то же, а это означает, что задана геометрическая прогрессии. Таким образом, сформулирован признак геометрической прогрессии, запишите его в таблицу. | Записывают во второй столбец: Если в последовательности b1, b2, b3,…,bn,…, каждый член, начиная со второго, равен среднему геометрическому двух соседних с ним членов: 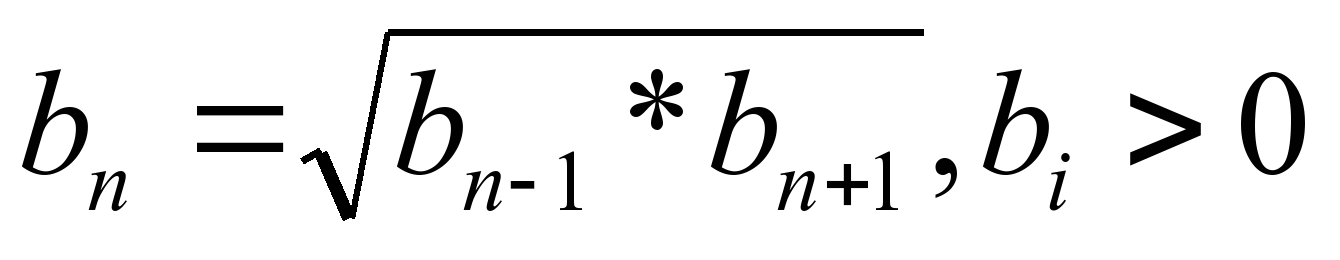 , n1 , n1 то такая последовательность является геометрической прогрессией |
| Раз для каждой из прогрессий верно прямое и обратное утверждение, можно сформулировать критерии арифметической и геометрической прогрессий. Данные критерии называются характеристическими свойствами арифметической и геометрической прогрессий соответственно. Сформулируйте их устно и запишите в канву-таблицу символьно.
| Формулируют и записывают: В первый столбец: Числовая последовательность а1, а2, а3,…,аn,…, является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предшествующего и последующего членов, то есть: а1, а2, а3,…,аn,… - арифметическая прогрессия 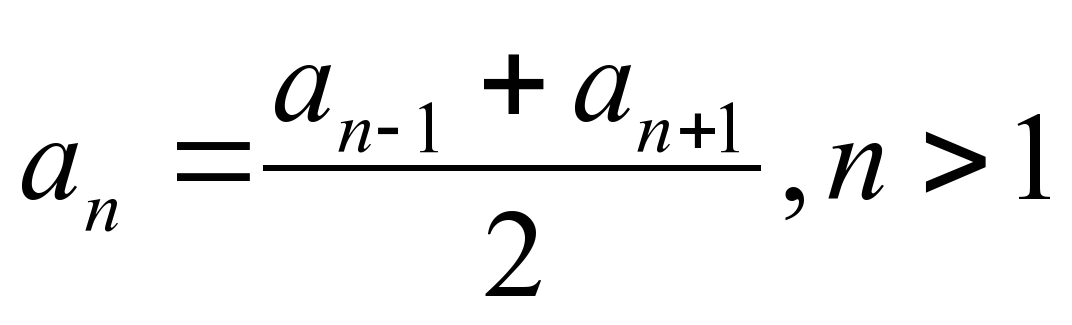 Во второй столбец: Числовая последовательность b1, b2, b3,…,bn,…, является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему геометрическому предшествующего и последующего членов, то есть: b1, b2, b3,…,bn,…, - геометрическая прогрессия 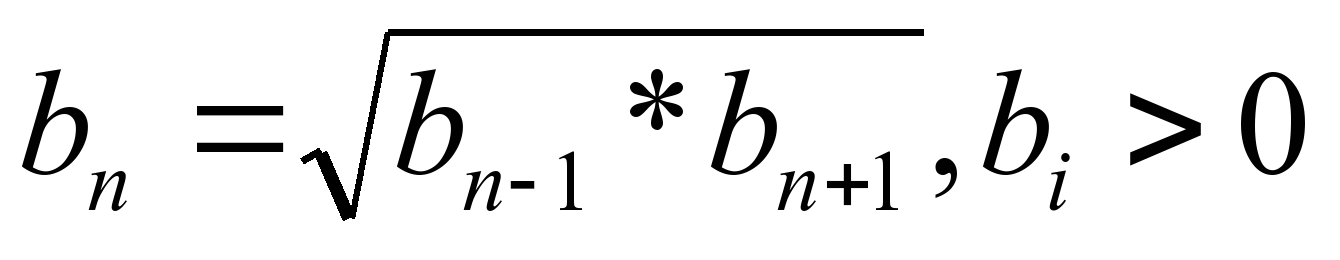 , n1 , n1 |
| Вновь рассмотрим определение арифметической прогрессии: заметим, что если заданы а1 и d, то остальные члены арифметической прогрессии можно найти по рекуррентной формуле аn+1=an+d. Таким способом нетрудно вычислить несколько первых членов последовательности, однако, например, для а50 уже потребуется много вычислений. Обычно для этого используется формула n-ого члена. Выведем ее для арифметической прогрессии. |
|
| Используя рекуррентную формулу, запишите 2-ой, 3-ий и 4-ый члены арифметической прогрессии. | а2=a1+d a3=a2+d a4=a3+d |
| Можно ли 3-ий член выразить через 1-ый? | a3=a2+d=a1+2d
|
| Можно ли 4-ый член выразить через 1-ый? | a4=a3+d=a1+3d
|
| Продолжая далее, таким способом можно выразить n-ый член арифметической прогрессии через первый член прибавлением к нему (n-1) раз числа d. | аn=a1+(n-1)d |
| Эта формула называется формулой n-ого члена арифметической прогрессии. Запишите ее в канву-таблицу. | Записывают в первый столбец: аn=a1+(n-1)d |
| Рассмотрим применение формулы на примере: Дана арифметическая прогрессия, найдите а16, если а1=3, d=5. | Подставим известные величины в формулу n-ого члена арифметической прогрессии, получим: а16=3+(16-1)ּ5=3+15ּ5=78 |
| Аналогично рассмотрим определение геометрической прогрессии: заметим, что если заданы b1 и q, то остальные члены геометрической прогрессии можно найти по рекуррентной формуле bn+1=bn*q. Таким способом нетрудно вычислить несколько первых членов последовательности, однако, например, для b25 уже потребуется много вычислений. Обычно для этого используется формула n-ого члена. Выведите ее аналогично формуле n-ого члена арифметической прогрессии. Запишите ее в канву-таблицу. | b2=b1*q b3=b2*q=b1*q2 b4=b3*q=b1*q3 и т.д. bn=b1*qn-1
Записывают во второй столбец: bn=b1*qn-1
|
| То есть n-й член геометрической прогрессии получается из первого члена умножением его (n-1) раз на q. |
|
| Таким образом, канва-таблица заполнена. На экране выводится заполненная канва-таблица | Учащиеся индивидуально проверяют заполненные таблицы. |
| III. Рефлексивно-оценочный этап |
| Какова была цель урока?
| Изучить 2 особых вида числовых последовательностей: дать им названия, сформулировать определения и изучить их свойства. |
| Достигли ли мы ее? | Да. |
| Как мы ее достигли? | На конкретных примерах выявили особые виды числовых последовательностей. Дали им названия, сформулировали определения, сформулировали и доказали их свойства. |
| Как называются выделенные особые виды последовательностей? | Арифметическая и геометрическая прогрессии. |
| Сформулируйте их определения и характеристические свойства. | Определения: Числовая последовательность а1, а2, а3,…,аn,…, называется арифметической прогрессией, если для всех натуральных n выполняются равенство: an+1=an+d, где d – разность. Числовая последовательность b1, b2, b3,…,bn,…, называется геометрической прогрессией, если для всех натуральных n выполняются равенство: bn+1=bn*q, где q – знаменатель. Характеристические свойства: Числовая последовательность а1, а2, а3,…,аn,…, является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предшествующего и последующего членов, то есть: а1, а2, а3,…,аn,… - арифметическая прогрессия 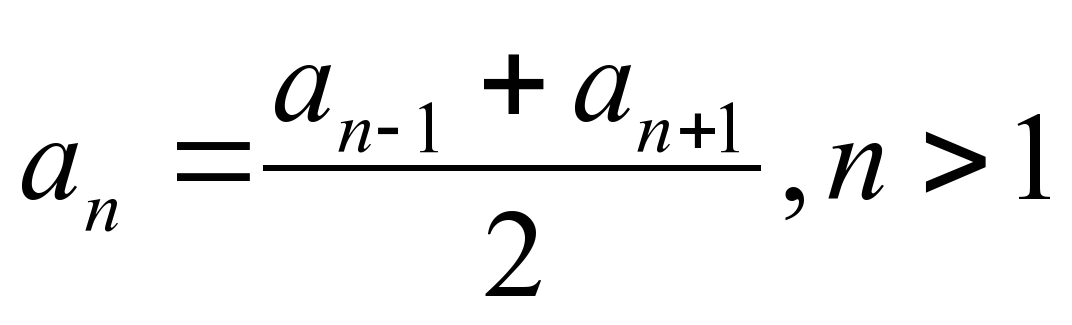 Числовая последовательность b1, b2, b3,…,bn,…, является геометрическая прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему геометрическому предшествующего и последующего членов, то есть: b1, b2, b3,…,bn,…, - геометрическая прогрессия 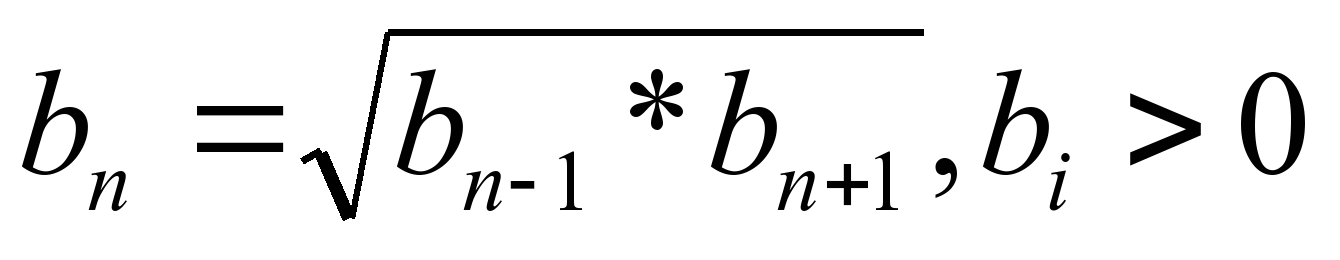 , n1 , n1 |
| Домашнее задание: выучить канву-таблицу, подготовиться к зачету. №№ 16.4 (в; г), 16.5 (в; г), 16.23 (в; г), 17.1 (в; г), 17.11 (в; г), 17.18 (в; г). (проговорить суть заданий) |
|