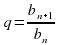Конспект урока "Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии"

Тема урока: Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии.

 Тип урока: Изучение нового материала.

Цель урока: Усвоить понятие геометрической прогрессии, вывести формулу n-го члена геометрической прогрессии, применить на практике полученные знания.

Задачи урока: Образовательные:

• расширить и углубить знания о числовых последовательностях; ввести определение геометрической прогрессии и вывести  формулу n-го члена геометрической прогрессии; ознакомить с понятиями возрастающей, убывающей и конечной геометрической прогрессии; показать практическое применение  понятия геометрической прогрессии и формулы n-го члена при решении задач.

Развивающие:

• развить аналитическое и логическое мышление; развивать зрительную память  и  произвольное внимание; развивать интеллектуальные умения: сравнивать, делать выводы, выявлять закономерности, анализировать.

Воспитательные: воспитывать

• правильную самооценку; культуру общения; ответственность; аккуратность;
• взаимопомощь.

Методы: объяснительно-иллюстративный, проблемный, репродуктивный.

Методическое обеспечение урока: учебник Латотина Л. А, Чеботаревский Б.Д. «Математика 9 класс»

Ход урока.

1.Организационный момент.

Эпиграф урока:

« Математические знания могут  приме­няться умело с пользой  лишь в том  слу­чае,

если они усвоены творчески»

         А.Н.Колмогоров

Обьясняет, что учащихся ждут на уроке новые математические знания, исследова­ния, интересные факты и открытия.

Познакомить учащихся с порядком работы на уроке. Сообщить тему урока, сформулировать совместную  цель деятельности.

2. Актуализация знаний учащихся. Проверка домашнего задания.

Актуализация знаний по темам: «Числовые последовательности», «Арифметическая прогрессия и ее свойства» - 3этап (5 минут).

1.Фронтальный опрос:

цель: подготовка к изучению нового материала на основе ранее изученного.

-Что называется числовой последовательностью?

-Назовите и охарактеризуйте способы задание числовой последовательности?

-Что называется разностью арифметической прогрессии?

-Какова формула n –го члена арифметической прогрессии?

-Приведите примеры арифметических прогрессий.

2.Самостоятельная работа (слайд 4):

цель: подведение к самостоятельному формулированию определения геометрической прогрессии путем создания проблемной ситуации.

-Вставьте  в числовую последовательность число вместо вопросительного знака:

   1) 7, ?, 13, 16

   2)  15,  19,  ?,  27

3. Изучение нового материала.

Известна задача-легенда, которая относится к началу нашей эры (встречается у ал-Беруни).

Шахматы – одна из самых древних игр. Она существует уже многие века и неудивительно, что с нею связаны различные придания, правдивость которых, за давностью времени, невозможно проверить.

     Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Царь Шерам позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку.

Изобретатель, его звали Сета, явился к трону повелителя.

      - Я желаю достойно вознаградить тебя.

       Мудрец молчал.

      - Я достаточно богат, чтобы исполнить твоё самое смелое пожелание. Назови награду, которая тебя удовлетворит.

- Повелитель,- сказал Сета,- прикажи выдать мне за первую клетку шахматной доски одно пшеничноё зерно, за вторую – 2, за третью - 4, за четвёртую – 8, за пятую – 16…

- Довольно, - с раздражением прервал его царь. – Ты получишь свои зёрна за всё 64 клетки доски. Но знай, что просьба твоя недостойна моей щедрости.

       Сета улыбнулся и покинул залу.

Отходя ко сну царь вспомнил об изобретателе шахмат и спросил:

-Унёс ли Сета свою жалкую награду?

- Повелитель,- ответили ему, математики твои трудятся без отдыха и надеются к рассвету закончит подсчёт.

Утром царю доложили, что число это так велико, что в его амбарах нет такого количества зёрен.

Здесь изложение легенды прерывается учителем, оставляя интригу для следующих уроков. Учащимся предлагается определить последовательность чисел и ее свойства.

? – Что за последовательность получилась?

1; 2; 4; 16; 32; 64; …

В этой последовательности каждый её член, начиная со второго, равен предыдущему, умноженному на 2. Такая последовательность называется геометрической.

Определение геометрической прогрессии.

Числовая последовательность b1 ;  b2 ;   b3 ;….;  bn;… называется геометрической прогрессией, если  для всех натуральных n выполняется равенство  bn+1 = bnq,    где bn ≠ 0, q – некоторое число, не равное нулю.     q называется знаменателем прогрессии.

Свойство геометрической прогрессии.

             bn+1 = bnq            bn-1 = bn : q

          Перемножим эти равенства

          bn+1∙ bn-1 = (bnq) ∙ (bn : q) = bn2

Последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого её члена, начиная со второго равен произведению двух соседних с ним членов.

•  все члены прогрессии положительны, то т. е. каждый член, начиная со второго, равен среднему геометрическому двух соседних с ним членов.

•  Этим объясняется название «геометрическая» прогрессия.

Формула n – го члена геометрической прогрессии.

bn+1 = bnq

                        b2 = b1q

                        b3 = b2q = b1q2

                        b4 = b3q = b1q3

                        …….

                         bn = b1qn-1

4. Практическое применение нового материала. Решение упражнений № 757, 759, 758(б,в), 760(г,д,е), 763, 770(б)

5. Подведение итогов урока. Рефлексия.

– Какие задачи стояли сегодня на уроке пе­ред нами? Выполнили мы их?

-Что мы узнали о геометри­ческой прогрессии?

-Какая числовая последова­тельность называется гео­метрической прогрессией?

-Какое число называется знаменателем геометриче­ской прогрессии?

-Какова формула n – го члена геометрической про­грессии?

6. Домашнее задание. П.19. №№ 758(а), 760(а-в), 770(а).

7.Заключительный этап урока.