Урок 75 алгебры Дата: 12.03.2015
8 класс
Тема урока:Повторение «Квадратичная функция и её график»
Цель: 1) систематизировать, обобщить знания по теме.
2) развивать качества мышления: гибкость, рациональность, критичность с учетом индивидуальных особенностей, развитие аргументированной математической речи, развитие математической зоркости, самостоятельности, познавательной активности, воспитание культуры учебного труда, аккуратности при построении графиков, чувства коллективизма, товарищества, ответственности за порученное дело; воспитание воли; упорства в достижении поставленной цели; умение контролировать внимание на всех этапах урока.
Тип урока: урок усвоения навыков и умений.
Формы обучения: групповая, индивидуальная.
Методы обучения: словесные, практические, иллюстративно-объяснительные, метод самостоятельной деятельности.
Оборудование: карточки с заданиями, интерактивная доска, тестирующие устройства ActiVote.
Технология: обучение в сотрудничестве.
План урока
1. Организационный момент. Цели и задачи урока.
2. Разминка.
3. Проверка теоретического материала.
4. Работа в группах.
5. Закрепление.
6. Тестирование
7. Рефлексия.
8. Домашнее задание.
9. Итоги урока.
Девиз нашего урока: «Дорогу осилит идущий, математику мыслящий!»
- Сегодня проведем обобщающий урок «По волнам функций»; подготовимся к контрольной работе по теме «Квадратичная функция и её график». Обращение к учащимся:
- получите 2 оценки, одну за работу на уроке, другую - за тест.
Что мы хотим получить от урока:
1. Знать формулы, задающие квадратичную функцию.
2. Уметь строить график любым способом.
3. Читать, т.е. исследовать график. функции.
4. Узнавать график квадратичной функции.
5. Выполнять алгебраические тождественные преобразования формул,задающих квадратичную функцию.
6. Как мы умеем сотрудничать и помогать друг другу.
Оборудование урока:
(под музыку: шум волны) (на экране волны)
I. Учитель: Представьте, что мы на море. 1-ая волна – «разминочная» Одолеем её под девизом: «уравнение- это золотой ключ, открывающий все математические сезамы».
Какие ученые математики занимались изучением уравнений, их классификацией, способами решения?
( Франсуа Виет и Фибоначчи).
Учитель:
Сегодня мы узнаем имя ещё одного математика.
Поиграем в «Поле чудес». Я читаю задание, а вы выбираете правильный ответ. (учитель ставит галочки)
А. 3х2-2х-5=0 Диофант – древнегреческий математик,
И. 7 х2 +14х = 0 год рождения и дата смерти до сих пор
Ф. Х2 -5х+6=0 не выяснены. Полагают, что он жил в 3в. до н.э
Т. х2-4=0
О. х2+4х+4=0
Н. 2 х2 -11х+5=0
Д. х2+2х= х2+6
1) Какое уравнение после алгебраических тождественных преобразований не будет квадратным? [Д]
2) Какое уравнение решается вынесением общего множителя за скобки? [и]
3) Какое уравнение можно решить, представляя в виде квадрата двучлена? [о]
4) Какое уравнение удобно решить по теореме Виета? [ф]
5) Какое уравнение решается по формуле четного второго коэффициента? [а]
6) В каком уравнении надо применять общую формулу корней? [н]
7) Какое уравнение можно решить разложением разности квадратов? [т]
- ДИОФАНТа можно охарактеризовать словами Госера:
Посредством уравнений, теорем.
Он уйму всяких разрешал проблем.
И засуху предсказывал, и ливни
Поистине его познанья дивны.
Вывод: Что показывают корни квадратных уравнений при исследовании квадратичной функции? (точки пересечения с осью Ох, то есть нули функции)
II. Перед нами теоретическая волна. Встретим её под девизом: «Усердие – мать удачи».
Пусть «морские звезды» принесут нам удачу (по 5 вопросов).
Каждая получает свою «морскую звезду» и каждый выбирает свой вопрос на удачу
1. Что мы называем функцией?
2. Определение квадратичной функции.
3. Что такое нули функции?
4. Что мы называет Д(f)?
III. «Практическая» волна – это похоже на 9-ый вал.
Наш девиз: «Обдумай цель раньше, чем дело начать».
Каждый получает свое задание и защищает работу по вертушке. (правила сотрудничества все помним?)
I. Построить график функций у=х2-4х+3 по алгоритму. В формуле, задающей квадратичную функцию, выделить полный квадрат двучлена.
II. Построить график функции у= (х-2)2-1 с помощью преобразований. Найти вершину параболы, нули функции, преобразовать функцию к виду у=ах2+вх+с
III. Построить график функции у=-х2+6х-5 по алгоритму. В формуле, задающей квадратичную функцию, выделить полный квадрат двучлена.
IV. Построить график функции у=-(х+3)2/2+2 с помощью преобразований. Найти вершину параболы, точки пересечения с осями координат, преобразовать функцию к виду у=ах2+вх+с.
(каждая группа защитилась по вертушке).
Итак, подведем итог: I и II. Сравнили графики своих функций. Какие способы построения графика квадратичной функции повторили? (по алгоритму,с помощью преобразований). Назовите наименьшее значение функции (-1).
III По своему графику назовите промежутки монотонности.
↑ на (-∞;3] ↓[3;+ ∞)
IV Назовите промежутки в которых функция у>0 и у<0
у>0 на (-5;-1) у<0 на (-∞;-5)U(-1;+ ∞)
-
IV. Волна «проверочная» - тестирование «Уверенность – залог успеха». Возьмите в руки тестировщикит Тест 1-10
V. Рефлексия
VI. Домашнее задание: тест из 10 заданий.
Оценочный лист
№
п/п
Ф.И.
Разминка
Теория
Сотрудничество
Закрепление
Итог
Тест
1
2
3
«Усердие – мать удачи».
Пусть «морские звезды» принесут нам удачу
Каждый получает свою «морскую звезду» и каждый выбирает свой вопрос на удачу
1. Что мы называем функцией?
2. Определение квадратичной функции.
3. Что такое нули функции?
4. Что мы называет Д(f)?
«Практическая» волна – это похоже на 9-ый вал.
Наш девиз: «Обдумай цель раньше, чем дело начать».
Каждый получает свое задание и защищает работу по вертушке. (правила сотрудничества все помним?)
I. Построить график функций у=х2-4х+3 по алгоритму. В формуле, задающей квадратичную функцию, выделить полный квадрат двучлена.
II. Построить график функции у= (х-2)2-1 с помощью преобразований. Найти вершину параболы, нули функции, преобразовать функцию к виду у=ах2+вх+с
III. Построить график функции у=-х2+6х-5 по алгоритму. В формуле, задающей квадратичную функцию, выделить полный квадрат двучлена.
IV. Построить график функции у=-(х+3)2/2+2 с помощью преобразований. Найти вершину параболы, точки пересечения с осями координат, преобразовать функцию к виду у=ах2+вх+с.
 лан урока
лан урока евиз нашего урока: «Дорогу осилит идущий, математику мыслящий!»
евиз нашего урока: «Дорогу осилит идущий, математику мыслящий!»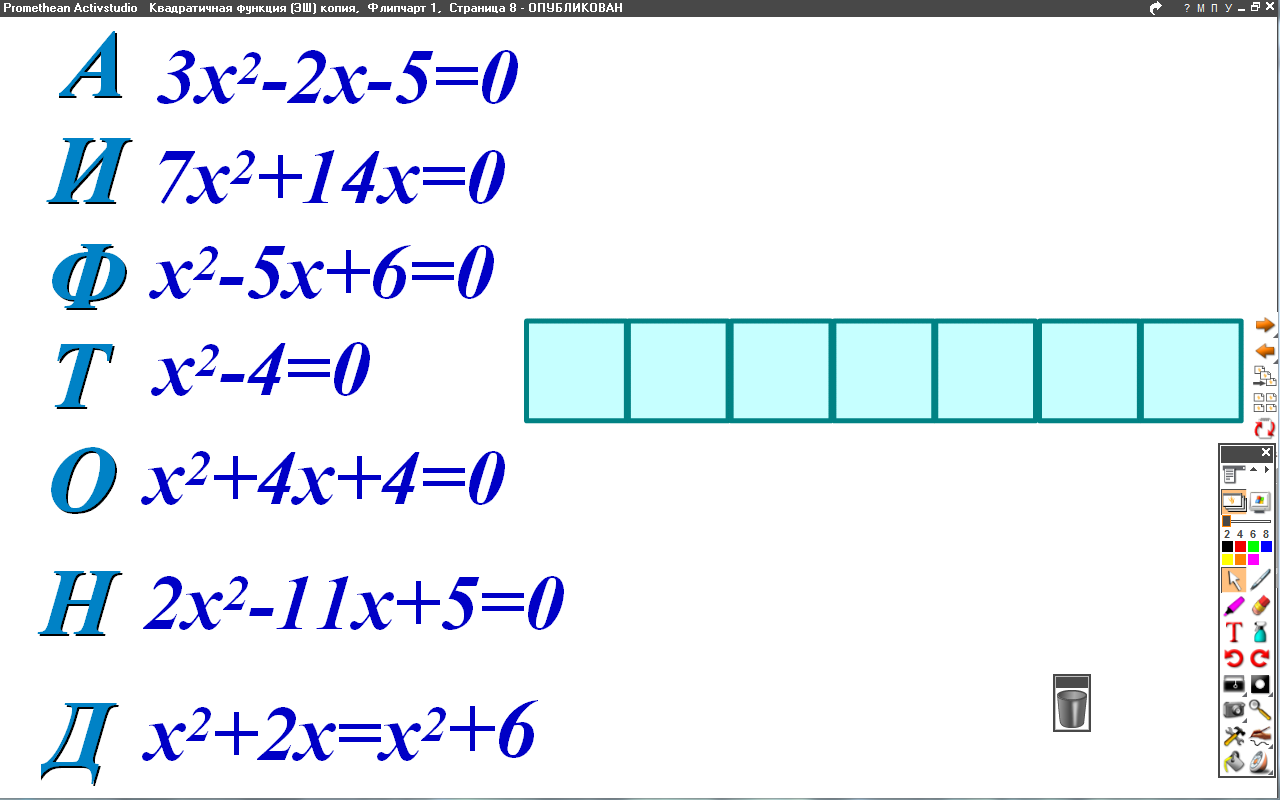 . 3х2-2х-5=0 Диофант – древнегреческий математик,
. 3х2-2х-5=0 Диофант – древнегреческий математик,  засуху предсказывал, и ливни
засуху предсказывал, и ливни