На этом и последующих занятиях мы будем решать графическим способом тригонометрические неравенства одного какого-то вида. Сегодня мы решим три тригонометрических неравенства вида sint<a. Вот они:
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Тригонометрические неравенства
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«тригонометрические неравенства »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2220 руб.
3170 руб.
1740 руб.
2480 руб.
1630 руб.
2330 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

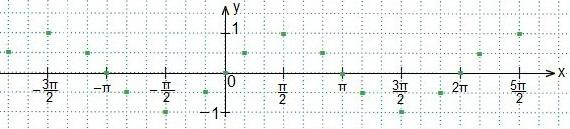
 Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду
Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду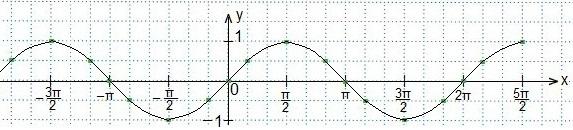 Проводим прямую.
Проводим прямую.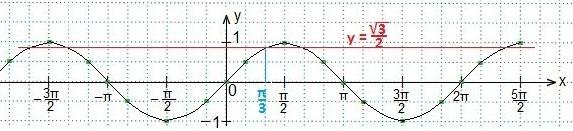


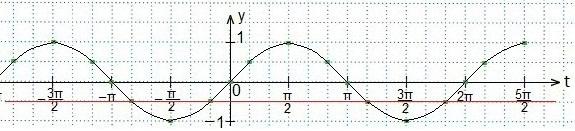
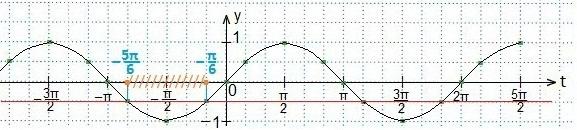
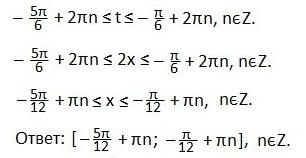 Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.
Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.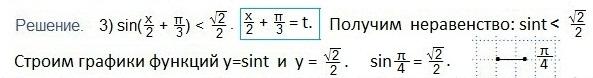
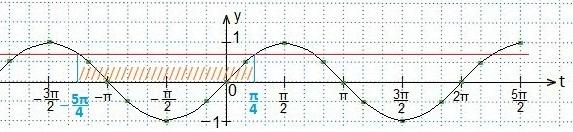
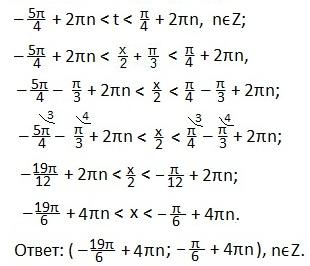 В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместоt подставим первоначальный аргумент синуса и будем выражать хиз полученного двойного неравенства.
В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместоt подставим первоначальный аргумент синуса и будем выражать хиз полученного двойного неравенства.















