В презентации рассматриваютсчя различные примеры решения простейших тригонометрических неравенств, изучаемых на уроках алгебры и начала анализа в 10 классе.Показывается один из способов решения неравенства с помощью тригонометрического круга, с записью ответа в виде числового промежутка на множестве , также показано, как можно решать тригонометрические неравенства с тангенсом или котангенсом, применяя ось тангенсов или ось котангенсов с последующей записью ответа, путём выделения решения на тригонометрическом круге.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация по теме " Тригонометрические неравенства"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого презентации
«тригонометрические неравенства»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
2230 руб.
3190 руб.
1670 руб.
2380 руб.
1900 руб.
2710 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

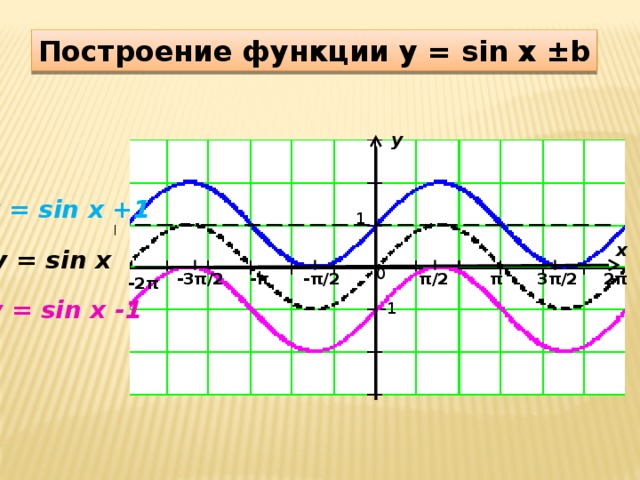
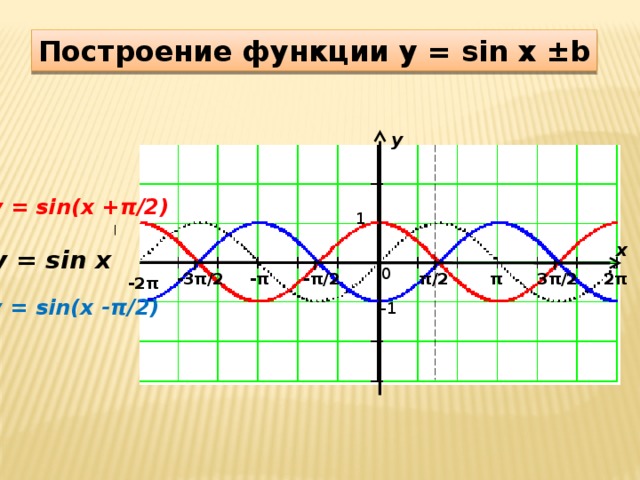
 0 при 0 + 2πn Z sin x Z 6. промежутки монотонности: x [- π / 2 + 2πn; π / 2 + 2πn], n Z – возрастает x [ π / 2 + 2πn; 3π / 2 + 2πn], n Z – убывает 7. экстремумы: y max = 1 при х = π / 2 + 2πn, n Z y min = - 1 при х = - π / 2 + 2πn, n Z 8. E(sin x) = [- 1 ; 1] 9. производная: (sin x )´ = cos x График функции y = sin x" width="640"
0 при 0 + 2πn Z sin x Z 6. промежутки монотонности: x [- π / 2 + 2πn; π / 2 + 2πn], n Z – возрастает x [ π / 2 + 2πn; 3π / 2 + 2πn], n Z – убывает 7. экстремумы: y max = 1 при х = π / 2 + 2πn, n Z y min = - 1 при х = - π / 2 + 2πn, n Z 8. E(sin x) = [- 1 ; 1] 9. производная: (sin x )´ = cos x График функции y = sin x" width="640"
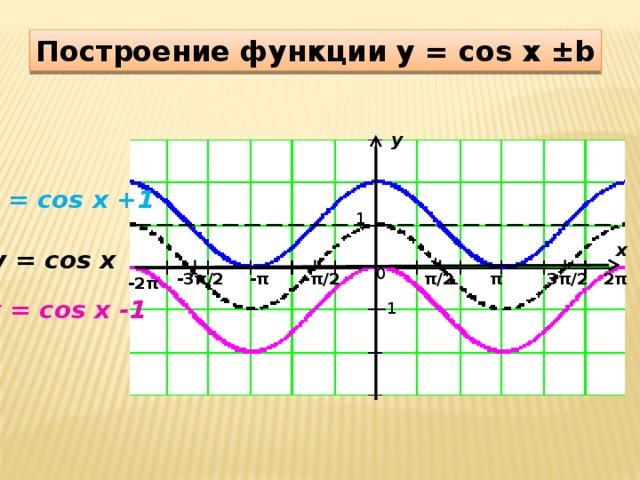
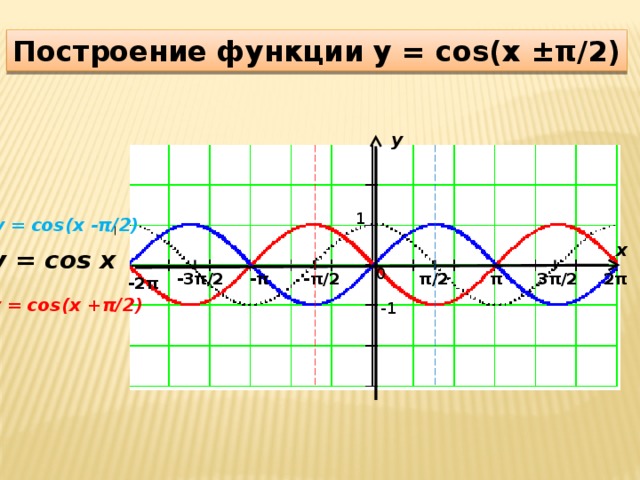
 0 при - π / 2 + 2πn π / 2 + 2πn, n Z cos x π / 2 + 2πn 3π / 2 + 2πn, n Z 6. промежутки монотонности: x [ π+ 2πn; 2π+ 2πn], n Z – возрастает x [0 + 2πn; π+ 2πn], n Z – убывает 7. экстремумы: y max = 1 при х = 2πn, n Z y min = - 1 при х = π+ 2πn, n Z 8. E(cos x) = [- 1 ; 1] 9. производная: (cos x )´ = - sin x График функции y = cos x" width="640"
0 при - π / 2 + 2πn π / 2 + 2πn, n Z cos x π / 2 + 2πn 3π / 2 + 2πn, n Z 6. промежутки монотонности: x [ π+ 2πn; 2π+ 2πn], n Z – возрастает x [0 + 2πn; π+ 2πn], n Z – убывает 7. экстремумы: y max = 1 при х = 2πn, n Z y min = - 1 при х = π+ 2πn, n Z 8. E(cos x) = [- 1 ; 1] 9. производная: (cos x )´ = - sin x График функции y = cos x" width="640"
 0 при 0 + πn π / 2 + πn, n Z tg x π / 2 + πn Z 6. промежутки монотонности: x [- π / 2 + πn; π / 2 + πn], n Z – возрастает экстремумов нет E(tg x) = R 9. производная: (tg x )´ = 1/cos 2 x График функции y = tg x" width="640"
0 при 0 + πn π / 2 + πn, n Z tg x π / 2 + πn Z 6. промежутки монотонности: x [- π / 2 + πn; π / 2 + πn], n Z – возрастает экстремумов нет E(tg x) = R 9. производная: (tg x )´ = 1/cos 2 x График функции y = tg x" width="640"
 0 при 0 + πn π / 2 + πn, n Z ctg x π / 2 + πn Z 6. промежутки монотонности: x [0+ πn; π+ πn], n Z – убывает экстремумов нет E(ctg x) = R 9. производная: (ctg x )´ = - 1/sin 2 x График функции y = ctg x" width="640"
0 при 0 + πn π / 2 + πn, n Z ctg x π / 2 + πn Z 6. промежутки монотонности: x [0+ πn; π+ πn], n Z – убывает экстремумов нет E(ctg x) = R 9. производная: (ctg x )´ = - 1/sin 2 x График функции y = ctg x" width="640"
















