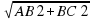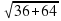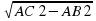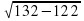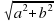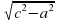План-конспект урока
по теме «Теорема Пифагора»
в 8-А классе
19 декабря 2014 г
Учитель: Кутовая Юлия Сергеевна
Цели: изучить теорему Пифагора и её доказательство. Научиться применять теорему для решения задач. Научиться выражать неизвестные стороны через известные значения. Существенно расширить круг геометрических задач, решаемых школьниками.
Познакомить учащихся с основными этапами жизни и деятельности Пифагора.
Осуществить предметную связь геометрии с алгеброй, географией, историей.
Задачи урока:
Образовательная: Создать условия для усвоения теоремы Пифагора и привитие навыков вычисления неизвестной стороны прямоугольного треугольника по 2-м известным сторонам; способствовать овладению навыками применять теорему Пифагора к решению простейших задач.
Развивающая: Способствовать развитию способности к сопоставлению, наблюдательности, внимания, развития способности к аналитикому мышлению, расширение кругозора.
Воспитательная: Формирование потребности в знаниях, интереса к математике.
Тип урока: Формирование новых знаний и умений.
Оборудование урока: Компьютер, мультимедийный проектор, экран, доска
Прогнозируемый результат:
1. Знать зависимость между сторонами прямоугольного треугольника.
2. Уметь доказывать теорему Пифагора.
3. Уметь применять теорему Пифагора для решения задач.
Эпиграф:
«… Геометрия обладает двумя сокровищами: одно из них – это теорема Пифагора….»
Иоганн Кеплер
План урока.
Организационный момент.
Проверка домашнего задания.
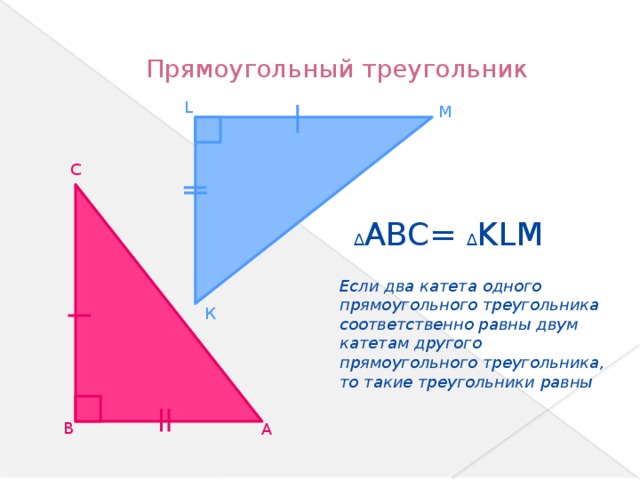
Актуализация знаний учащихся по темам, «Прямоугольный треугольник», «Площадь», «Признак равенства прямоугольных треугольников по двум катетам».
Историческая справка о построении прямого угла в Древнем Египте.
Формулировка и доказательство теоремы Пифагора.
Историческая справка о Пифагоре.
Альтернативные доказательства теоремы Пифагора.
Закрепление и первичный контроль знаний.
Итоги урока и домашнее задание.
Ход урока.
Организационный момент.
Приветствие, проверка готовности учащихся к уроку, организация внимания.
Проверка домашнего задания.
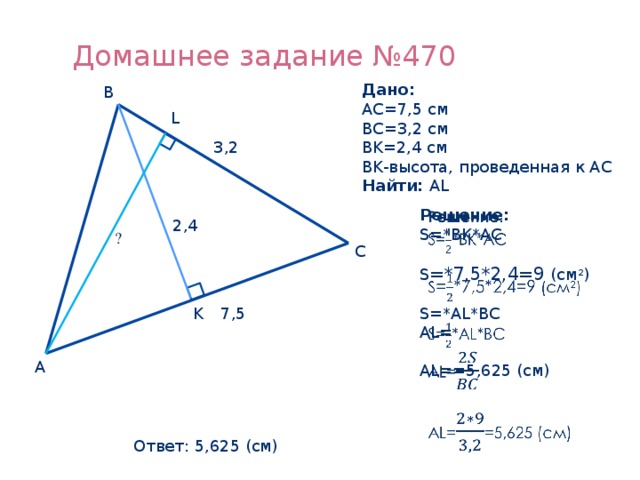
№470
Дано:
AC=7,5 см
BC=3,2 см
BK=2,4 см
BK-высота, проведенная к AC
Найти: AL
Решение:
S=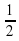 *BK*AC
*BK*AC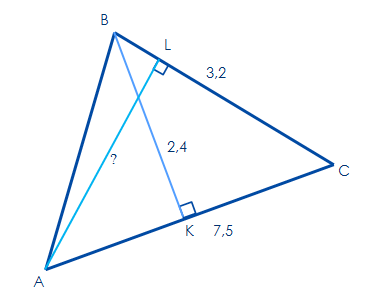
S=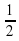 *7,5*2,4=9 (см2)
*7,5*2,4=9 (см2)
S=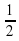 *AL*BC
*AL*BC
AL=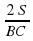
AL=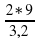 =5,625 (см)
=5,625 (см)
Актуализация знаний.
А)
Что изображено?
Как называются стороны, образующие прямой угол?
Как называется сторона, лежащая против прямого угла?
Чему равна площадь этого треугольника?
Чему равна сумма острых углов в данном треугольнике?
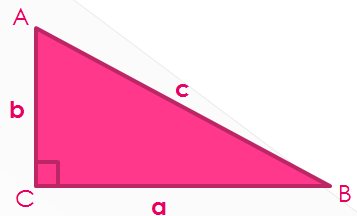
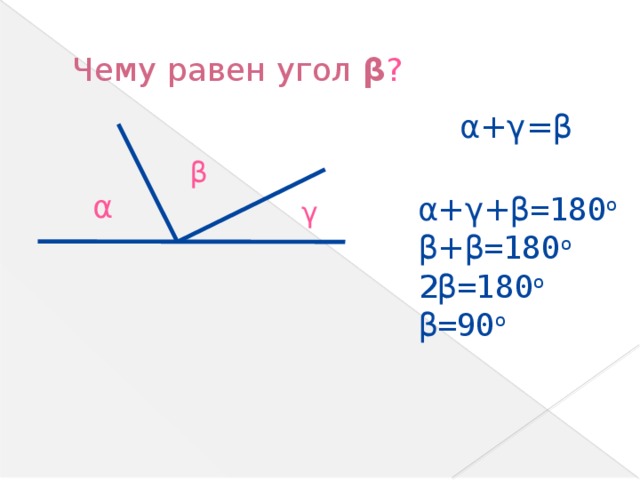
Б) Чему равен угол β?
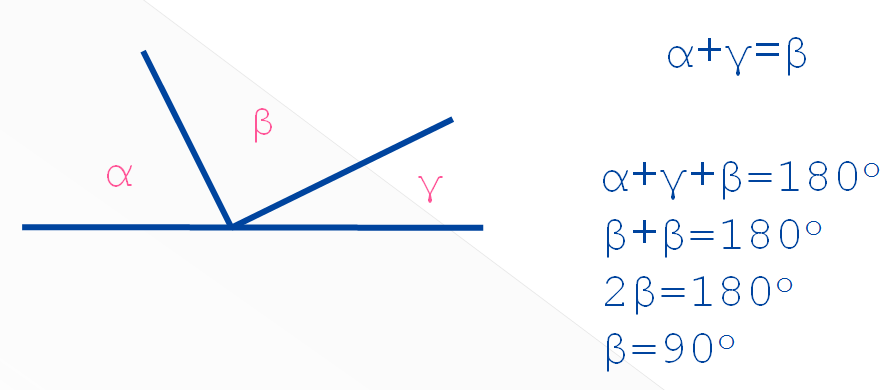
В) Вспомнить признак равенства двух прямоугольных треугольников по двум катетам.
Отсюда следует, что для прямоугольного треугольника гипотенуза совершенно точно определена и не может быть равна одному или другому числу. Т.е. существует закон, который определяет зависимость длины гипотенузы от длины катетов.
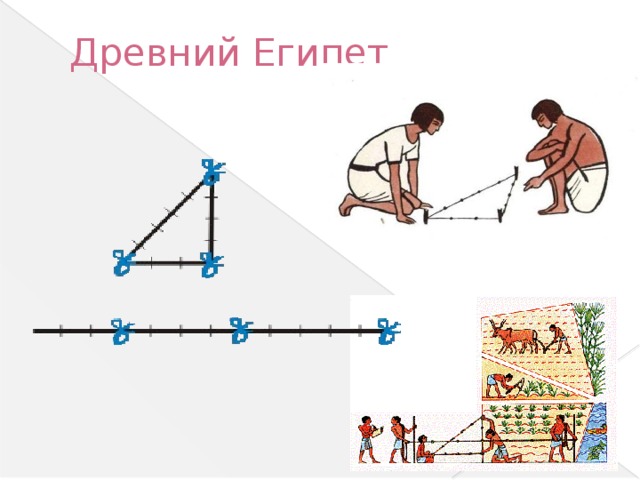
Историческая справка о построении прямого угла в Древнем Египте.
Общепринято мнение, что египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид.
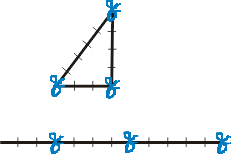
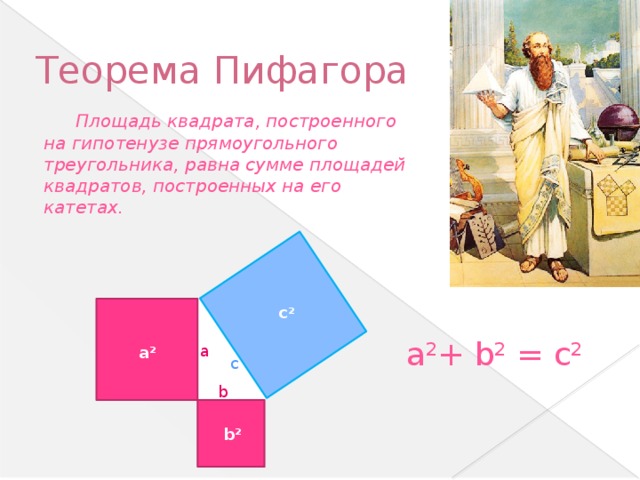
Теорема Пифагора и её доказательство.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a2+ b2= c2
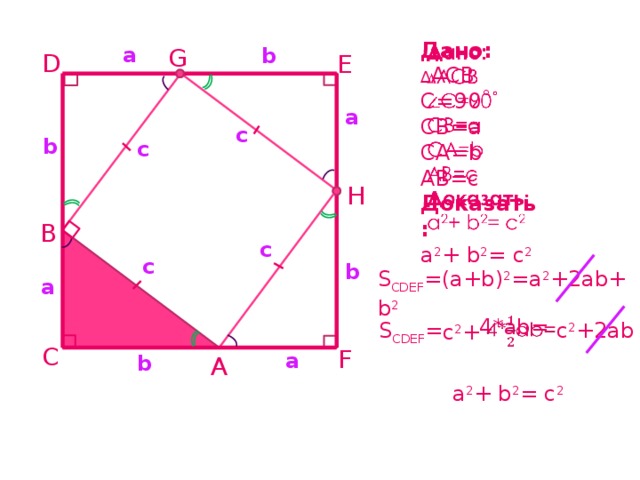
Дано:
∆ACB,  C=90˚,
C=90˚,
CB=a, CA=b, AB=c
Доказать:
a2+ b2= c2
Доказательство: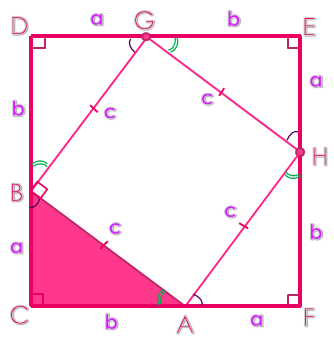
SCDEF=(a+b)2=a2+2ab+b2
SCDEF=c2+4*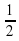 ab=c2+2ab
ab=c2+2ab
a2+ b2= c2
Историческая справка о Пифагрре (готовит ученик).
Пифагор – древнегреческий философ, математик, политический, религиозный деятель. Его родиной был остров Самос (отсюда и прозвище - Самосский), где он появился на свет приблизительно в 580 г. до н. э.
Его одаренность проявилась уже в раннем возрасте.
Образование у Пифагора было очень хорошим, юношу обучало много наставников.
За свою жизнь он побывал в Египте, Вавилоне и Индии, где он учился и осваивал науки, в том числе и математику.
В итоге в Греции Пифагор организовал собственную школу, которая была одновременно и политической структурой, и религиозной, с очень строгими правилами. Все ученики не должны были употреблять мясную пищу, раскрывать другим учение своего наставника.
Погиб Пифагор во время восстания в Греции в возрасте 90 лет.
Поскольку Пифагор считал свое учение тайной и практиковал только устную передачу его ученикам, собрания сочинений после него не осталось. Помимо доказательства теоремы Пифагора, этому математику приписывают подробное изучение целых чисел, пропорций и их свойств. Пифагорейцам принадлежит значительная заслуга в придании геометрии характера науки.
Альтернативные доказательства теоремы Пифагора.
-Доказательство Евклида.

Площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Данное доказательство также получило название «Пифагоровы штаны».
-Шаржи и стихи

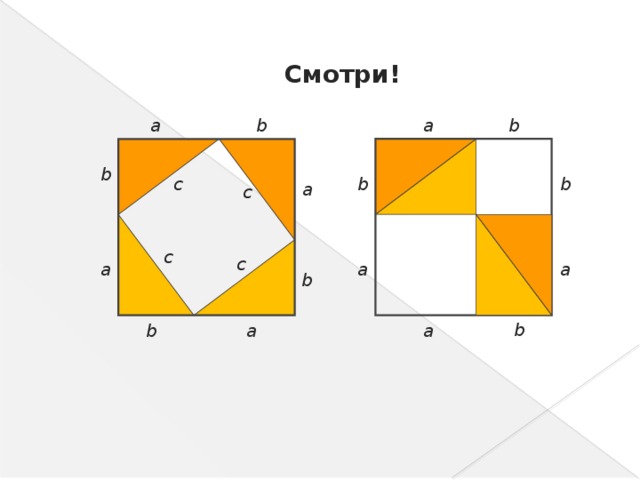
-Доказательство пифагорейцев – «Без слов»
Смотри!
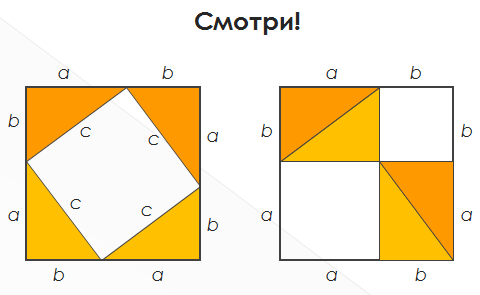
Закрепление и первичный контроль знаний.
Алгоритм решения задач.
указать прямоугольный треугольник
записать для него теорему Пифагора
выразить неизвестную сторону через две другие
подставить известные значения и вычислить неизвестную сторону
Решение задач.
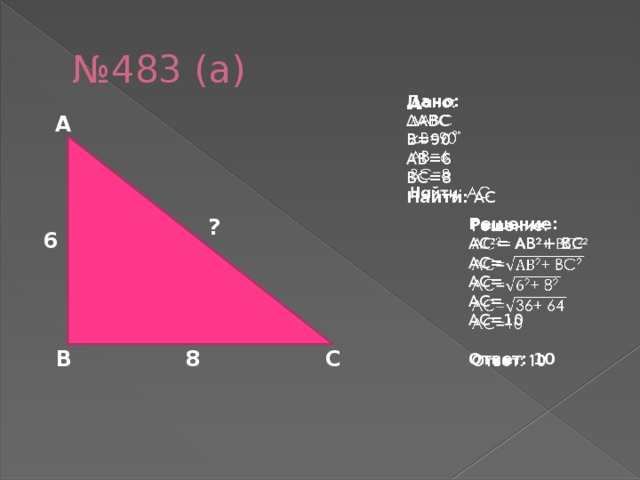
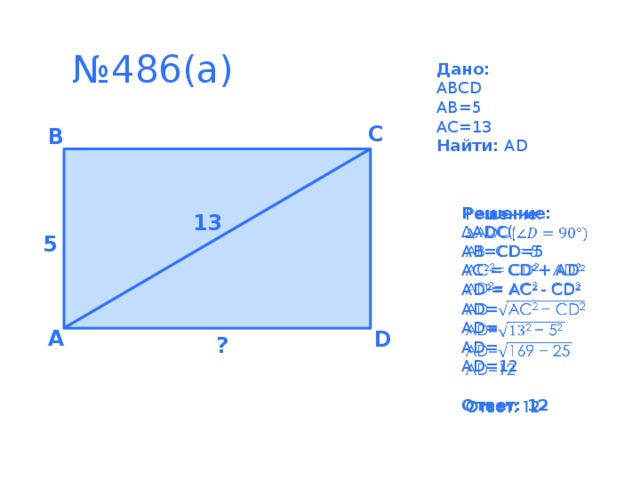
№483(а)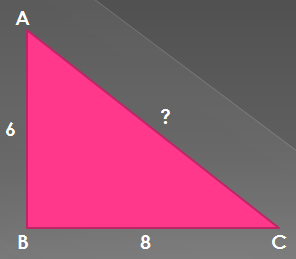
Дано:
∆ABC,  B=90˚, AB=6, BC=8
B=90˚, AB=6, BC=8
Найти: AC
Решение:
AC2= AB2+ BC2
AC=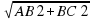
AC=
AC=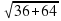
AC=10
Ответ: 10
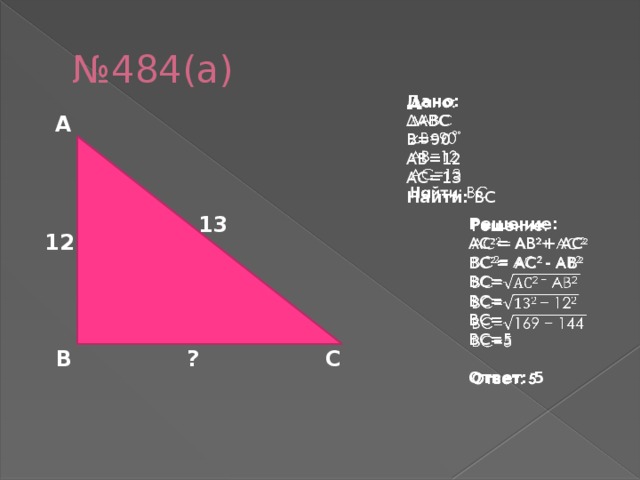
№484(а)
Дано: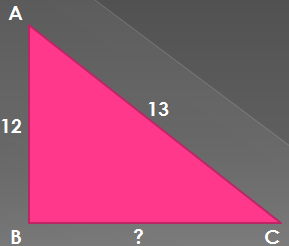
∆ABC,  B=90˚, AB=12, AC=13
B=90˚, AB=12, AC=13
Найти: BC
Решение:
AC2= AB2+ AC2
BC2= AC2 - AB2
BC=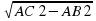
BC=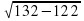
BC=
BC=5
Ответ: 5
Итоги урока и домашнее задание.
Что понравилось?
Чему научились?
Познакомились с теоремой Пифагора:
a2+ b2= c2
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Научились выражать неизвестные стороны через известные значения.
с=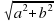
b=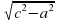
a=
Познакомились с основными фактами из биографии Пифагора.
- Домашнее задание: §3, п.55, с 128, №483(б,в)
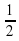 *BK*AC
*BK*AC
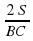
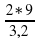 =5,625 (
=5,625 (


 C=90˚,
C=90˚,